Дифференциальное уравнение Бернулли. Примеры решений

Предпраздничные новогодние дни предвещают зачеты и экзамены, поэтому в срочном порядке я решил порадовать читателей еще одним уроком по теме Дифференциальные уравнения первого порядка. Речь пойдет о так называемых уравнениях Бернулли, которые нет-нет, да и встречаются в практических работах и контрольных заданиях. Уравнение Бернулли рекомендую изучать только в том случае, если у вас уже есть опыт решения дифференциальных уравнений первого порядка, в особенности, следует хорошо ориентироваться в линейных неоднородных уравнениях вида .

Дифференциальное уравнение Бернулли имеет вид:

Очевидно – уравнение Бернулли по общей структуре напоминает линейное неоднородное уравнение первого порядка.

Характерным признаком, по которому можно определить уравнения Бернулли, является наличие функции «игрек» в степени «эн»: .

Если или , то уравнение Бернулли превращается в уравнения, которые вы уже должны уметь решать.

Целая степень может быть как положительной, так и отрицательной (во втором случае получится дробь), кроме того, может быть обыкновенной дробью, например .

Как и линейное неоднородное уравнение первого порядка, уравнение Бернулли может приходить на новогодний утренник в разных костюмах. Волком:

Зайчиком:

Или белочкой:

Важно, чтобы в уравнении присутствовал персонаж , который, как я только что показал, иногда может маскироваться под корень.

Обратите внимание, что одним из очевидных решений уравнения Бернулли (если ) является решение: . Действительно, если найти и подставить в уравнения рассмотренных типов, то получится верное равенство. Как отмечалось в статье об однородных уравнениях, если по условию требуется найти только частное решение, то функция по понятной причине нас не морозит, но вот когда требуется найти общее решение/интеграл, то необходимо проследить, чтобы эту функцию не потерять!

Все популярные разновидности уравнения Бернулли я принёс в большом мешке с подарками и приступаю к раздаче. Развешивайте носки под ёлкой.

Пример 1

Найти частное решение дифференциального уравнения, соответствующее заданному начальному условию.
,

Наверное, многие удивились, что первый подарок сразу же извлечён из мешка вместе с задачей Коши. Это не случайность. Когда для решения предложено уравнение Бернулли, почему-то очень часто требуется найти частное решение. По своей коллекции я провёл случайную выборку из 10 уравнений Бернулли, и общее решение (без частного решения) нужно найти всего в двух уравнениях. Но, собственно, это мелочь, поскольку общее решение придётся искать в любом случае.

Решение: данный диффур имеет вид , а значит, является уравнением Бернулли

Как решить дифференциальное уравнение Бернулли?

Алгоритм достаточно прост и незамысловат.

На первом шаге нужно избавиться от «игрека» в правой части. Для этого сбрасываем в низ левой части и проводим почленное деление:

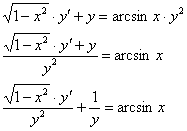
Далее необходимо избавиться от игрека вот в этом слагаемом:

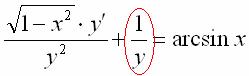
Для этого проводим замену: , то есть меняем дробь с «игреком» на букву «зет».
Находим производную:
.
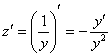Если данное действие не понятно, пожалуйста, посмотрите первый параграф урока Производные неявной и параметрически заданной функций.

Смотрим на первое слагаемое:

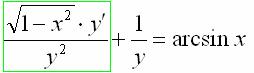
И что-то подсказывает, что нужно заменить .
Это легко: если , то

Таким образом, в результате проведенной замены уравнение превращается в уравнение:

Получено линейное неоднородное уравнение первого порядка. С той лишь разницей, что вместо привычного «игрека» у нас буква «зет».

Вывод: уравнение Бернулли с помощью замены сводится к линейному неоднородному уравнению первого порядка

Я сменю у каждого слагаемого знак, делать это не обязательно, просто запись будет выглядеть стандартнее что ли:

Дальше алгоритм работает по накатанной колее, важно только уметь решать неоднородное уравнение 1-го порядка:

Проведем замену:

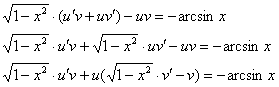
Составим и решим систему:

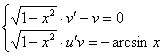
Из первого уравнения найдем :

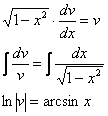
– подставим найденную функцию во второе уравнение системы:

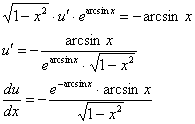
Подобные интегралы я ласково называю дурными интегралами, они не столько сложные, сколько творческие – нужно догадаться (хотя бы научным тыком), как их решать.

Данный интеграл берётся по частям:

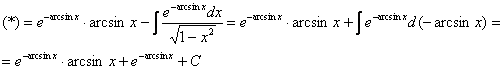
Творчество присутствует, помимо интегрирования по частям, использован метод подведения функции под знак дифференциала.

Таким образом:

Но это ещё не всё, выполняем обратную замену:
Если изначально было , то обратно будет

В результате получаем общее решение исходного уравнения Бернулли:

Тривиальное решение потерялось (это произошло в самом начале при делении на ) и не вошло в общий интеграл. Однако это обстоятельство нас совершенно не волнует, поскольку по условию требовалось решить только задачу Коши (! заметьте, что если бы условие требовало указать в ответе и общее решение, то его следовало бы дополнить функцией ). Найдем частное решение, удовлетворяющее начальному условию :

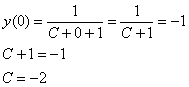
Ответ: частное решение:

Для мастодонтов дифференциального исчисления вкратце напоминаю алгоритм проверки дифференциального уравнения:

1) проверяем, выполнено ли начальное условие;
2) берём ответ и находим производную ;
3) подставляем ответ и найденную производную в исходное ДУ – должно получиться верное равенство.

Проверить дифференциальное уравнение Бернулли действительно не всем под силу, так как в большинстве случаев приходится находить трудную производную и выполнять громоздкую подстановку.

Когда я подбирал первый пример для этой статьи, то очень хотелось разобрать распространенное уравнение Бернулли в духе , однако сразу же после замены оно становится до неприличия похоже на Пример 8 урока неоднородные дифференциальные уравнения первого порядка. Поэтому пусть лучше будет что-нибудь необычное.

Но, вы не расстраивайтесь, вот пара более простых примеров для самостоятельного решения:

Пример 2

Найти решение ДУ , удовлетворяющее начальному условию

Пример 3

Найти решение задачи Коши
,

Полные решения и ответы в конце урока.

В третьем примере перед решением целесообразно представить уравнение в стандартном виде: .

Вообще, иногда составители сборников и методичек зашифровывают уравнения до неузнаваемости, например:

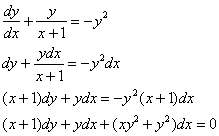
Как говорится, сиди студент и разгадывай ребус – какого ~~хрена~~ типа этот диффур. То ли уравнение с разделяющимися переменными, то ли уравнение в полных дифференциалах, то ли еще какое-нибудь уравнение.

Интереснейшая задача и новая информация, о которой я до сих пор не рассказывал:

Пример 4

Найти решение ДУ , соответствующее начальному условию

Корни, куда же без них.

Решение: пожалуйста, классический вид уравнения Бернулли.

По условию требуется решить только задачу Коши, поэтому ось абсцисс снова идёт лесом.

Сначала убираем «игрек» из правой части, для этого делим каждую часть на :

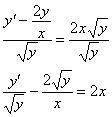
Теперь с помощью замены нужно избавиться от «игрека» вот в этом слагаемом:

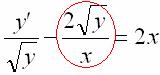
Из вышесказанного следует замена:
Найдем производную:
, откуда выразим:

Таким образом:

Получено линейное неоднородное уравнение, проведем замену:

Составим и решим систему: .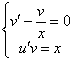

Из первого уравнения найдем :

– подставим во второе уравнение:

Таким образом: и в результате обратной замены получаем общий интеграл , из которого легко выразить общее решение:

Найдем частное решение, соответствующее заданному начальному условию :

…Вот тебе и раз! Уравнение имеет два корня и в результате получаются… два частных решения? Нет. Когда мы выражали общее решение, то выполнили возведение в квадрат, из-за чего у нас появился посторонний корень. Поэтому начальное условие лучше подставить непосредственно в общий интеграл :

– и помещаем этот ноль уже в общее решение :

Легко видеть, что значению соответствует частный интеграл , и он не удовлетворяет начальному условию .

Вот так-то оно бывает! – в статье об однородных уравнениях мы рассмотрели случаи потери решений, а оказывается, «решение» можно ещё и «приобрести».

Ответ: частное решение – проверку выполните самостоятельно, она тут устная.

И сейчас ещё один любопытный факт. Семейство кривых (общий интеграл ДУ) располагается в верхней полуплоскости и касается оси абсцисс в каждой её точке. Образно говоря, множество графиков (при всех действительных значениях константы) своими точками касания порождает решение , которое, как заправский партизан засело в чаще леса и в общее решение не вошло.

Такое необычное решение называют особым решением дифференциального уравнения.
В общем случае особое решение тоже представляет собой кривую, которая огибает «основное семейство», но в рассмотренном примере оно – есть прямая, которая ассоциируется с «подставкой» под графики функций .

Конец факта. И начало следующих :)

Возможно, некоторые удивились, почему я ничего не рассказал про математика Бернулли. Забыл. Не будем нарушать традиций. Якоб Бернулли почти итальянец, жил в Швейцарии, говорил на пяти языках. В семье Бернулли 9 (!) математиков, причём у некоторых представителей династии есть серьёзные достижения и в области физики. …Пожалуй, этой информации будет достаточно, а то мне в голову стал приходить крайне неэтичный юмор в духе «Якоб, Иоганн – какая студенту разница?» =) …Походил немного по комнате, посмеялся, продолжаю:

Пример 5

Найти общее решение (или общий интеграл) дифференциального уравнения первого порядка.

Немногочисленный пример из моей выборки, когда требуется найти только общее решение. Полное решение и ответ в конце урока.

Мы рассмотрели наиболее распространенные версии уравнения Бернулли – с «игреком» во второй степени и с «игреком» под квадратным корнем. Другие варианты встречаются реже. Разберём пример, когда «игрек» находится в кубе.

Пример 6

Найти общее решение дифференциального уравнения

Решение: данное ДУ является уравнением Бернулли.

Очевидно, что является решением этого уравнения.

И только после этой оговорки делим обе части на :

Избавляемся от «игрека» в «полюбившемся» слагаемом, для этого проведем замену:

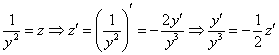
В результате:

Получено линейное уравнение, проведем замену:

Решим систему:

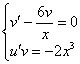
Из первого уравнения найдем :

– подставим во второе уравнение:

Таким образом:

Проведём обратную замену: если изначально , то обратно:

В принципе, здесь можно выразить общее решение в виде:
, но, согласитесь, смотрится не очень…, словно Дедушка Мороз подсунул в подарок гнилую мандаринку. Эта фишка уже рассматривалась мной на уроке Однородные дифференциальные уравнения первого порядка. Нет-нет, испорченные продукты питания никому не предлагал =)

Лично я в похожей ситуации почти всегда склоняюсь к тому, чтобы оставить ответ в виде общего интеграла (заодно париться не нужно).

Ответ: общий интеграл: . Ещё одно решение:

Перед кремлёвским салютом рассмотрим заключительный пример с отрицательной степенью.

Пример 7

Найти частное решение дифференциального уравнения
,

Это пример для самостоятельного решения.

Ну вот, мешок с подарками пуст, надеюсь все остались довольны. Хотя, честно, Новый Год не люблю, сегодня вычитал на Анекдоте.ру меткий афоризм: 10 дней праздников обычно проводишь либо без всякой пользы либо с большим вредом.

Отличной вам сессии!

Решения и ответы:

Пример 2. Решение: данное ДУ является уравнением Бернулли. Найдем общее решение.

Проведем замену:

Получено линейное неоднородное уравнение, замена: .

Составим и решим систему:
Из первого уравнения найдем :

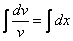
– подставим во второе уравнение:

Таким образом:
Обратная замена:
Общее решение:
Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение:
Красиво.

Пример 3. Решение:
Данное дифференциальное уравнение является уравнением Бернулли, разделим обе части на :

Проведем замену:

Получено линейное неоднородное уравнение, проведем замену:

Составим и решим систему:

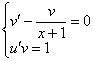
Из первого уравнения найдем :

– подставим во второе уравнение:

Таким образом:

Обратная замена:
Общее решение:
Найдем частное решение, соответствующее заданному начальному условию:

Ответ: частное решение:

Пример 5. Решение: данное уравнение является уравнением Бернулли.
Очевидно, что является решением данного уравнения.

Замена:

В полученном линейном неоднородном уравнении, проведем замену:

Решим систему: .
Из первого уравнения найдем :

– подставим во второе уравнение:

Таким образом:
Общее решение:
Обратная замена:

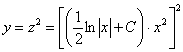
Ответ: общее решение ; ещё одно решение:

Пример 7. Решение:
Данное ДУ является уравнением Бернулли.

Проведем замену:

Получено линейное неоднородное уравнение, проведем замену:

Составим и решим систему:

Из первого уравнения найдем :

– подставим во второе уравнение:

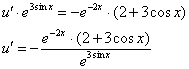
Таким образом:

Обратная замена:
Частное решение, соответствующее начальному условию , можно найти прямо из общего интеграла . Для этого вместо «икса» подставляем ноль, а вместо «игрека» – единицу:

Таким образом, частное решение:

Частное решение также выясняется и более «привычным» способом через общее решение .