


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Выпуклость, вогнутость и точки перегиба графика
Локомотив исследования функции неумолимо приближает нас к конечной станции, и после освоения непрерывности, области определения, интервалов знакопостоянства, асимптот, интервалов монотонности и экстремумов функции осталось узнать, как найти интервалы выпуклости / вогнутости графика и его точки перегиба. Также иногда это идёт и отдельным заданием. Поэтому танцуют все.
Начнём с нашей любимой физкультуры. Пожалуйста, встаньте и наклонитесь вперёд. Либо назад. Это выпуклость. Теперь вытяните руки перед собой ладонями вверх и представьте, что держите большое бревно на груди… …Если не нравится бревно, пусть будет ещё что / кто-нибудь =) Это вогнутость. В ряде источников встречаются синонимичные термины выпуклость вверх и выпуклость вниз, но я сторонник коротких названий.
! Внимание: некоторые авторы определяют выпуклость и вогнутость с точностью до наоборот. Это математически тоже верно, но по обывательски некорректно, ибо все представляют «выпуклую линзу» и «вогнутую кровать».
Формальное определение выпуклости и вогнутости графика достаточно труднО для чайника, поэтому ограничимся геометрической интерпретацией понятия на конкретных примерах. Рассмотрим график функции ![]() , которая непрерывна на всей числовой прямой:
, которая непрерывна на всей числовой прямой:
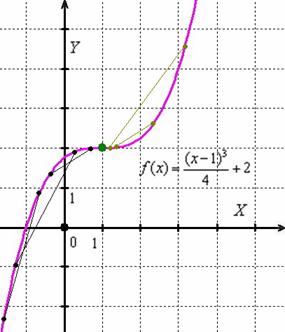
Его легко построить с помощью геометрических преобразований, и, наверное, многие читатели в курсе, как он получен из кубической параболы.
Назовём хордой отрезок, соединяющий две различные точки графика.
График функции является выпуклым на некотором интервале, если он расположен не ниже любой хорды данного интервала. Подопытная линия выпукла на ![]() , и, очевидно, что здесь любая часть графика расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных отрезка.
, и, очевидно, что здесь любая часть графика расположена НАД своей хордой. Иллюстрируя определение, я провёл три чёрных отрезка.
График функции являются вогнутым на интервале, если он расположен не выше любой хорды этого интервала. В рассматриваемом примере пациент вогнут на промежутке ![]() . Пара коричневых отрезков убедительно демонстрирует, что тут и любой кусок графика расположен ПОД своей хордой.
. Пара коричневых отрезков убедительно демонстрирует, что тут и любой кусок графика расположен ПОД своей хордой.
Точка графика, в которой он меняет выпуклость на вогнутость или вогнутость на выпуклость, называется точкой перегиба. У нас она в единственном экземпляре (первый случай), причём, на практике под точкой перегиба можно подразумевать как зелёную точку ![]() , принадлежащую самой линии, так и «иксовое» значение
, принадлежащую самой линии, так и «иксовое» значение ![]() .
.
ВАЖНО! Перегибы графика следует изображать аккуратно и очень плавно. Недопустимы всевозможные «неровности» и «шероховатости». И тут дело за небольшой тренировкой.
Второй подход к определению выпуклости / вогнутости в теории даётся через касательные:
Выпуклый на интервале график расположен не выше касательной, проведённой к нему в произвольной точке данного интервала. Вогнутый же на интервале график – не ниже любой касательной на этом интервале.
Гипербола ![]() вогнута на интервале
вогнута на интервале ![]() и выпукла на
и выпукла на ![]() :
:
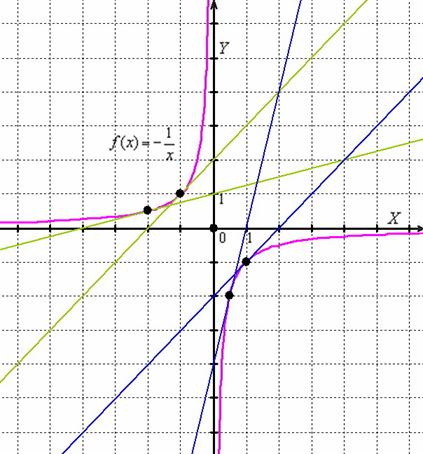
При переходе через начало координат вогнутость меняется на выпуклость, однако точку ![]() НЕ СЧИТАЮТ точкой перегиба, так как функция
НЕ СЧИТАЮТ точкой перегиба, так как функция ![]() не определена в ней.
не определена в ней.
Более строгие утверждения и теоремы по теме можно найти в учебнике, а мы переходим к насыщенной практической части:
Как найти интервалы выпуклости, интервалы вогнутости
и точки перегиба графика?
Материал прост, трафаретен и структурно повторяет исследование функции на возрастание / убывание и экстремумы.
Выпуклость / вогнутость графика характеризует вторая производная функции.
Пусть функция ![]() дважды дифференцируема на некотором интервале. Тогда:
дважды дифференцируема на некотором интервале. Тогда:
– если вторая производная ![]() на интервале, то график функции
на интервале, то график функции ![]() является выпуклым на данном интервале;
является выпуклым на данном интервале;
– если вторая производная ![]() на интервале, то график функции
на интервале, то график функции ![]() является вогнутым на данном интервале.
является вогнутым на данном интервале.
На счёт знаков второй производной есть доисторическая ассоциация:
«–» показывает, что «в график функции нельзя налить воду» (выпуклость),
а «+» – «даёт такую возможность» (вогнутость).
Необходимое условие перегиба
Если в точке ![]() есть перегиб графика функции
есть перегиб графика функции ![]() , то
, то ![]() либо значения
либо значения ![]() не существует (случай разберём позже, читайте!).
не существует (случай разберём позже, читайте!).
Данная фраза подразумевает, что функция ![]() непрерывна в точке
непрерывна в точке ![]() и в случае
и в случае ![]() – дважды дифференцируема в некоторой её окрестности.
– дважды дифференцируема в некоторой её окрестности.
Обратное справедливо не всегда. То есть из равенства ![]() (либо небытия значения
(либо небытия значения ![]() ) ещё не следует существования перегиба графика функции
) ещё не следует существования перегиба графика функции ![]() в точке
в точке ![]() . Он может существовать. Или не существовать. Но и в той и в другой ситуации
. Он может существовать. Или не существовать. Но и в той и в другой ситуации ![]() называют критической точкой второй производной.
называют критической точкой второй производной.
Достаточное условие перегиба
Если вторая производная ![]() при переходе через точку
при переходе через точку ![]() меняет знак, то в данной точке существует перегиб графика функции
меняет знак, то в данной точке существует перегиб графика функции ![]() .
.
Логично.
Точек перегиба может не быть вовсе, и в этом смысле показательны некоторые элементарные образцы. Проанализируем вторую производную функции ![]() :
:
![]()
Получена положительная функция-константа, то есть для любого значения «икс» ![]() . И в самом деле, парабола
. И в самом деле, парабола ![]() вогнута на всей области определения, точки перегиба отсутствуют. Легко заметить, что отрицательный коэффициент при
вогнута на всей области определения, точки перегиба отсутствуют. Легко заметить, что отрицательный коэффициент при ![]() «переворачивает» параболу и делает её выпуклой (о чём нам сообщит вторая производная – отрицательная функция-константа).
«переворачивает» параболу и делает её выпуклой (о чём нам сообщит вторая производная – отрицательная функция-константа).
Экспоненциальная функция ![]() также вогнута на
также вогнута на ![]() :
:
![]()
![]() для любого значения «икс».
для любого значения «икс».
Точек перегиба у графика ![]() , разумеется, нет.
, разумеется, нет.
Исследуем на выпуклость / вогнутость график логарифмической функции ![]() :
:
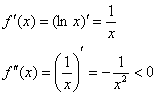
Таким образом, ветка логарифма является выпуклой на интервале ![]() . Вторая производная
. Вторая производная ![]() определена и на промежутке
определена и на промежутке ![]() , но рассматривать его НЕЛЬЗЯ, поскольку данный интервал не входит в область определения функции
, но рассматривать его НЕЛЬЗЯ, поскольку данный интервал не входит в область определения функции ![]() . Требование очевидно – коль скоро там нет графика логарифма, то ни о какой выпуклости / вогнутости / перегибах речи, естественно, не заходит.
. Требование очевидно – коль скоро там нет графика логарифма, то ни о какой выпуклости / вогнутости / перегибах речи, естественно, не заходит.
Как видите, всё действительно очень напоминает историю с возрастанием, убыванием и экстремумами функции. Похож и сам алгоритм исследования графика функции ![]() на выпуклость, вогнутость и наличие перегибов:
на выпуклость, вогнутость и наличие перегибов:
1) На первом шаге находим область определения функции ![]() и точки разрыва.
и точки разрыва.
2) Разыскиваем критические значения. Для этого берём вторую производную ![]() и решаем уравнение
и решаем уравнение ![]() . Точки, в которых не существует 2-й производной, но которые входят в область определения самой функции – тоже считаются критическими!
. Точки, в которых не существует 2-й производной, но которые входят в область определения самой функции – тоже считаются критическими!
3) Отмечаем на числовой прямой все найденные точки разрыва и критические точки (если они есть ). Методом интервалов определяем знаки ![]() на полученных интервалах. Как только что пояснялось, рассматривать следует только те промежутки, которые входят в область определения функции
на полученных интервалах. Как только что пояснялось, рассматривать следует только те промежутки, которые входят в область определения функции ![]() . Делаем выводы о выпуклости / вогнутости и точках перегиба графика функции
. Делаем выводы о выпуклости / вогнутости и точках перегиба графика функции ![]() . Даём ответ.
. Даём ответ.
Попытайтесь устно применить алгоритм для функций ![]() . Во втором случае, кстати, пример, когда в критической точке не существует перегиба графика. Впрочем, начнём с ненамного более сложных заданий:
. Во втором случае, кстати, пример, когда в критической точке не существует перегиба графика. Впрочем, начнём с ненамного более сложных заданий:
Пример 1
Найти интервалы выпуклости, вогнутости и точки перегиба графика
![]()
Решение:
1) Функция определена и непрерывна на всей числовой прямой. Очень хорошо.
2) Найдём вторую производную. Можно предварительно выполнить возведение в куб, но гораздо выгоднее продифференцировать сложную функцию:
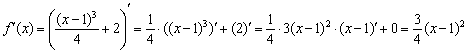
Заметьте, что ![]() , а значит, функция является неубывающей. Хоть это и не относится к заданию, но на такие факты всегда желательно обращать внимание.
, а значит, функция является неубывающей. Хоть это и не относится к заданию, но на такие факты всегда желательно обращать внимание.
![]()
Найдём критические точки второй производной:
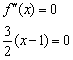
![]() – критическая точка
– критическая точка
3) Проверим выполнение достаточного условия перегиба. Определим знаки второй производной на полученных интервалах ![]() .
.
Внимание! Сейчас работаем со второй производной (а не с функцией!)
Используем метод интервалов. Повторим его ещё разок.
Выберем наиболее выгодную точку ![]() интервала
интервала ![]() и вычислим в ней значение второй производной:
и вычислим в ней значение второй производной:
![]() , следовательно,
, следовательно, ![]() в любой точке интервала
в любой точке интервала ![]() .
.
Из интервала ![]() возьмём значение
возьмём значение ![]() и проведём аналогичное действие:
и проведём аналогичное действие:
![]() , а значит,
, а значит, ![]() и на всём интервале
и на всём интервале ![]() .
.
В результате получены следующие знаки второй производной:

Таким образом, график САМОЙ ФУНКЦИИ ![]() является выпуклым на интервале
является выпуклым на интервале ![]() и вогнутым на
и вогнутым на ![]() . При переходе через
. При переходе через ![]() вторая производная меняет знак, поэтому в данной точке существует перегиб графика.
вторая производная меняет знак, поэтому в данной точке существует перегиб графика.
Найдём ординату: ![]()
Ответ: график функции выпукл на интервале ![]() и вогнут на
и вогнут на ![]() , в точке
, в точке ![]() существует перегиб графика.
существует перегиб графика.
Как вариант, пойдёт и запись «…в точке ![]() существует перегиб графика».
существует перегиб графика».
Пример 2
Найти интервалы выпуклости, вогнутости и точки перегиба графика
![]()
Это пример для самостоятельного решения. Примерный образец оформления задания в конце урока. А чертежи – в начале =)
Рассмотрим более интересных представителей мира функций:
Пример 3
Найти интервалы выпуклости, вогнутости и точки перегиба графика
![]()
Решение:
1) Функция определена и непрерывна на ![]() .
.
2) Найдём критические точки второй производной:
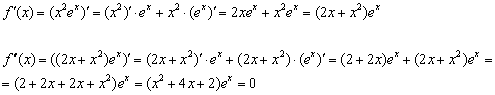
Так как ![]() , то корни могут появиться только из решения квадратного уравнения:
, то корни могут появиться только из решения квадратного уравнения:
![]()
Дискриминант положителен, и на подходе две критические точки:
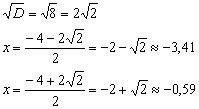
Как и в ситуации с экстремумами функции, критические точки рациональнее не нумеровать подстрочными индексами. Ну а то, что они получились с радикалами – обычное дело.
3) Определим знаки второй производной. Можно использовать стандартный метод интервалов, но здесь ![]() , и учитывая, что
, и учитывая, что ![]() – парабола, ветви которой направлены вверх, получаем:
– парабола, ветви которой направлены вверх, получаем:

Таким образом, график функции ![]() является выпуклым на интервале
является выпуклым на интервале ![]() и вогнутым на
и вогнутым на ![]() . В обеих критических точках существуют перегибы графика (т. к. 2-я производная при переходе через них меняет знак).
. В обеих критических точках существуют перегибы графика (т. к. 2-я производная при переходе через них меняет знак).
Найдём ординаты данных точек:
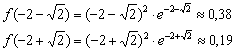
Ответ: график функции выпуклый на интервале ![]() и вогнутый на
и вогнутый на ![]() . В точках
. В точках ![]() существуют перегибы графика.
существуют перегибы графика.
Чтобы закомментировать некоторые важные моменты нарисую его полностью:
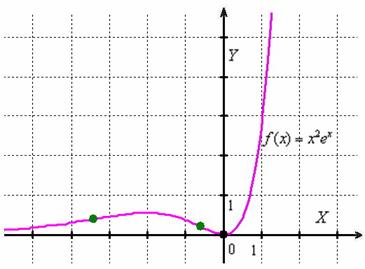
Прежде всего, ещё раз подчёркиваю необходимость аккуратно выполнять чертежи: слева график вогнут. Кстати, обратите внимание, что там он не может быть выпуклым, поскольку линия бесконечно близко прижимается к своей горизонтальной асимптоте. Когда аналитически получается подобный противоречивый результат, приходится перепроверять асимптоты, интервалы возрастания / убывания, выпуклости / вогнутости.
При переходе через левую зелёную точку график начинает плавно выгибаться вверх – и до второй точки у нас интервал выпуклости. Затем снова следует плавный прогиб вниз и на крайнем правом интервале имеет место вогнутость графика.
Более простое задание для самостоятельного решения:
Пример 4
Найти интервалы выпуклости, вогнутости и точки перегиба графика
![]()
Особенность предложенной функции состоит в её чётности, а это значит, что интервалы выпуклости / вогнутости и точки перегибы графика (если они существуют) симметричны относительно оси ![]() . И если, например, на крайнем левом интервале получится выпуклость, а на крайнем правом вогнутость, следовательно, где-то допущена ошибка. Примерный образец решения + чертёж для наглядности – в конце урока.
. И если, например, на крайнем левом интервале получится выпуклость, а на крайнем правом вогнутость, следовательно, где-то допущена ошибка. Примерный образец решения + чертёж для наглядности – в конце урока.
Читателям со средним и высоким уровнем подготовки (да и чайникам тоже) рекомендую попутно исследовать возрастание / убывание и экстремумы функций – ведь в рассматриваемых заданиях вынужденно фигурируют первые производные! Комплексный подход быстрее научит проводить полное исследование функций и понимать, как выглядят их графики.
Настал черёд популярных…, правильно догадались, дробно-рациональных:
Пример 5
Исследовать график функции ![]() на выпуклость, вогнутость и перегибы.
на выпуклость, вогнутость и перегибы.
Решение:
1) Функция терпит бесконечные разрывы в точках ![]() , и это обстоятельство крайне важно для решения задачи.
, и это обстоятельство крайне важно для решения задачи.
2) Найдём критические точки второй производной.
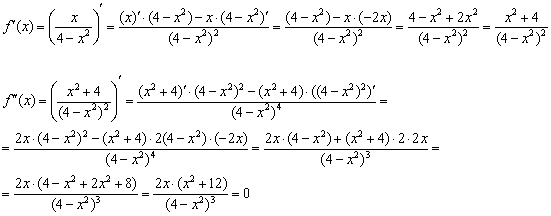
Пополните свой арсенал рациональной методикой упрощения второй производной: числитель и знаменатель сокращаем на ![]() , множитель
, множитель ![]() выносим за скобки. А в случае возникновения трудностей с нахождением самих производных, целесообразно перебазироваться в соседний раздел сайта и поднять свою технику дифференцирования.
выносим за скобки. А в случае возникновения трудностей с нахождением самих производных, целесообразно перебазироваться в соседний раздел сайта и поднять свою технику дифференцирования.
В результате получена одна критическая точка: ![]() .
.
3) Отметим на числовой прямой две точки разрыва, критическую точку и определим знаки второй производной на полученных интервалах:

Напоминаю важный приём метода интервалов, позволяющий значительно ускорить решение. Вторая производная ![]() получилась весьма громоздкой, поэтому не обязательно рассчитывать её значения, достаточно сделать «прикидку» на каждом интервале. Выберем, например, точку
получилась весьма громоздкой, поэтому не обязательно рассчитывать её значения, достаточно сделать «прикидку» на каждом интервале. Выберем, например, точку ![]() , принадлежащее левому промежутку,
, принадлежащее левому промежутку,
и выполним подстановку:
![]()
Теперь анализируем множители:
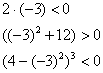
Два «минуса» и «плюс» дают «плюс», поэтому ![]() , а значит, вторая производная положительна и на всём интервале
, а значит, вторая производная положительна и на всём интервале ![]() .
.
Закомментированные действия несложно выполнить устно. Кроме того, множитель ![]() выгодно игнорировать вообще – он положителен при любом «икс» и не оказывает влияния на знаки нашей второй производной.
выгодно игнорировать вообще – он положителен при любом «икс» и не оказывает влияния на знаки нашей второй производной.
Итак, какую информацию нам предоставила ![]() ?
?
Ответ: график функции ![]() является вогнутым на
является вогнутым на ![]() и выпуклым на
и выпуклым на ![]() . В начале координат (ясно, что
. В начале координат (ясно, что ![]() ) существует перегиб графика.
) существует перегиб графика.
При переходе через точки ![]() вторая производная тоже меняет знак, но они не считаются точками перегиба, так как функция
вторая производная тоже меняет знак, но они не считаются точками перегиба, так как функция ![]() терпит в них бесконечные разрывы.
терпит в них бесконечные разрывы.
В разобранном примере первая производная ![]() сообщает нам о росте функции на всей области определения. Всегда бы такая халява =) Кроме того, очевидно наличие трёх асимптот
сообщает нам о росте функции на всей области определения. Всегда бы такая халява =) Кроме того, очевидно наличие трёх асимптот ![]() . Данных получено много, что позволяет с высокой степенью достоверности представить внешний вид графика. До кучи, функция ещё и нечётная. Исходя из установленных фактов, попытайтесь выполнить набросок на черновике. Картинка в конце урока.
. Данных получено много, что позволяет с высокой степенью достоверности представить внешний вид графика. До кучи, функция ещё и нечётная. Исходя из установленных фактов, попытайтесь выполнить набросок на черновике. Картинка в конце урока.
Задание для самостоятельного решения:
Пример 6
Исследовать график функции ![]() на выпуклость, вогнутость и найти точки перегиба графика, если они существует.
на выпуклость, вогнутость и найти точки перегиба графика, если они существует.
Чертежа в образце нет, но гипотезу выдвинуть не возбраняется ;)
Шлифуем материал, не нумеруя пункты алгоритма:
Пример 7
Исследовать график функции ![]() на выпуклость, вогнутость и найти точки перегиба, если они существует.
на выпуклость, вогнутость и найти точки перегиба, если они существует.
Решение: функция терпит бесконечный разрыв в точке ![]() .
.
У нас как обычно, всё отлично:
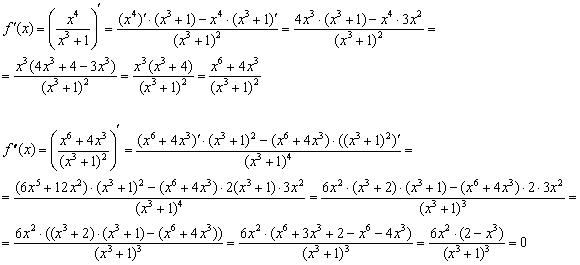
Производные не самые трудные, главное быть внимательным с их «причёской».
В наведённом марафете обнаруживаются две критические точки второй производной:
![]()
Определим знаки ![]() на полученных интервалах:
на полученных интервалах:

В точке ![]() существует перегиб графика, найдём ординату точки:
существует перегиб графика, найдём ординату точки:
![]()
При переходе через точку ![]() вторая производная не меняет знак, следовательно, в ней НЕТ перегиба графика.
вторая производная не меняет знак, следовательно, в ней НЕТ перегиба графика.
Ответ: интервалы выпуклости: ![]() ; интервал вогнутости:
; интервал вогнутости: ![]() ; точка перегиба:
; точка перегиба: ![]() .
.
Рассмотрим заключительные примеры с дополнительными примочками:
Пример 8
Найти интервалы выпуклости, вогнутости и точки перегиба графика
![]()
Решение: с нахождением области определения особых проблем не возникает:
![]() , при этом в точках
, при этом в точках ![]() функция терпит разрывы.
функция терпит разрывы.
Идём проторенной дорогой:
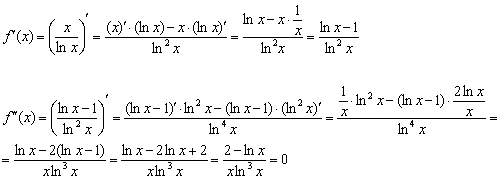
![]() – критическая точка.
– критическая точка.
Определим знаки ![]() , при этом рассматриваем интервалы только из области определения функции:
, при этом рассматриваем интервалы только из области определения функции:

В точке ![]() существует перегиб графика, вычислим ординату:
существует перегиб графика, вычислим ординату:
![]()
Ответ: график ![]() является выпуклым на
является выпуклым на ![]() и вогнутым на
и вогнутым на ![]() , в точке
, в точке ![]() существует перегиб.
существует перегиб.
Пример 9
Сильно маньячить не будем – то же задание для функции ![]() .
.
Рекомендую следующий порядок действий:
– в методичке Графики элементарных функций ищем график арккосинуса, полагаю, интервалы выпуклости / вогнутости и точку перегиба видно неплохо.
– анализируя геометрические преобразования, выясняем, как сдвинется график, если к аргументу функции добавлена двойка;
– в принципе, понятна область определения ![]() , но её академичнее найти аналитическим путём, похожие примеры разобраны в конце указанного урока;
, но её академичнее найти аналитическим путём, похожие примеры разобраны в конце указанного урока;
– на завершающем этапе, собственно, выполняем задание, при этом поведение второй производной нужно изучить только в найденной области определения функции ![]() .
.
Полное решение и ответ в конце урока.
Как отмечалось в теоретической части статьи, бывает ситуация, когда функция определена в некоторой точке, однако вторая производная в ней не определена. Такая точка считается критической (но только один этот факт и здесь не гарантирует наличие перегиба!).
Например, график функции ![]() терпит перегиб в начале координат, хотя второй производной там не существует. Тем не менее, в точке
терпит перегиб в начале координат, хотя второй производной там не существует. Тем не менее, в точке ![]() строго выполнено и необходимое и достаточное условие перегиба. Желающие могут убедиться в этом самостоятельно.
строго выполнено и необходимое и достаточное условие перегиба. Желающие могут убедиться в этом самостоятельно.
Похожий случай с более трудной функцией ![]() и её первой производной
и её первой производной ![]() рассмотрен в Примере 8 урока об экстремумах функции (откройте на соседней вкладке – там есть график). Не поленился, прямо сейчас нашёл
рассмотрен в Примере 8 урока об экстремумах функции (откройте на соседней вкладке – там есть график). Не поленился, прямо сейчас нашёл ![]() (вроде как правильно). На числовой прямой откладываем выколотые критические точки
(вроде как правильно). На числовой прямой откладываем выколотые критические точки ![]() второй производной. Анализ
второй производной. Анализ ![]() на полученных интервалах показывает, что при переходе через точку
на полученных интервалах показывает, что при переходе через точку ![]() (остриё) знак 2-й производной не меняется (перегиба нет), а вот в точке
(остриё) знак 2-й производной не меняется (перегиба нет), а вот в точке ![]() есть перегиб графика (хотя
есть перегиб графика (хотя ![]() и не существует).
и не существует).
Теперь у вас есть всё необходимое оружие и доспехи для генерального сражения с графиками функций!
Решения и ответы:
Пример 2. Решение:
1) Функция терпит бесконечный разрыв в точке ![]()
2) Найдём критические точки второй производной:
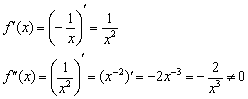
Критические точки отсутствуют.
3) Определим знаки второй производной на полученных интервалах:

Ответ: график функции ![]() является вогнутым на интервале
является вогнутым на интервале ![]() и выпуклым на
и выпуклым на ![]() , точки перегиба отсутствуют.
, точки перегиба отсутствуют.
Пример 4. Решение:
1) Функция определена и непрерывна на ![]() .
.
2) Найдём критические точки второй производной:
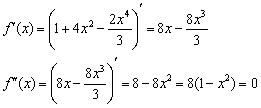
![]() – критические точки
– критические точки
3) Определим знаки второй производной на полученных интервалах:

В точках ![]() существуют перегибы графика.
существуют перегибы графика.
![]()
Ответ: график функции ![]() является вогнутым на интервале
является вогнутым на интервале ![]() и выпуклым на
и выпуклым на ![]() , точки перегиба:
, точки перегиба: ![]() .
.
Науки ради:
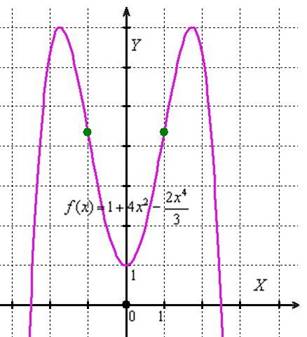
График Примера 5:
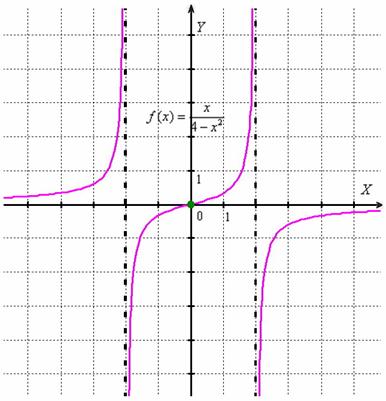
Пример 6. Решение: найдём критические точки второй производной:
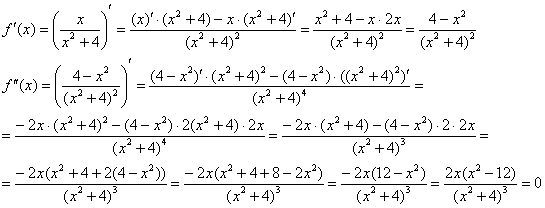
![]() – критические точки:
– критические точки:
Определим знаки второй производной на полученных интервалах:

Во всех трёх точках существуют перегибы графика.
![]()
Ответ: график функции выпуклый на ![]() и вогнутый на
и вогнутый на ![]() . В точках
. В точках ![]() существуют перегибы графика.
существуют перегибы графика.
Пример 9. Решение: найдём область определения функции. Составим и решим двойное неравенство:
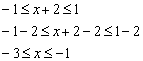
Таким образом, ![]() .
.
Найдём критические точки второй производной:
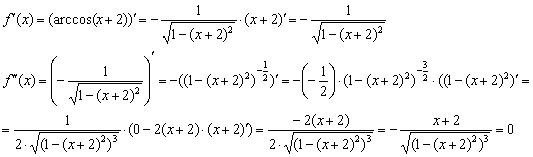
![]() – критическая точка.
– критическая точка.
Учитывая область определения функции, определим знаки ![]() :
:

В точке ![]() существует перегиб графика.
существует перегиб графика.
![]()
Ответ: интервал вогнутости графика: ![]() , выпуклости:
, выпуклости: ![]() , точка перегиба:
, точка перегиба: ![]() .
.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright