


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Векторное произведение векторов.
Смешанное произведение векторов
На данном уроке мы рассмотрим ещё две операции с векторами: векторное произведение векторов и смешанное произведение векторов (сразу ссылки для страждущих). Ничего страшного, так иногда бывает, что для полного счастья, помимо скалярного произведения векторов, требуется ещё и ещё. Такая вот векторная ненасытность. Может сложиться впечатление, что мы залезаем в дебри аналитической геометрии. Это не так. В данном разделе высшей математики вообще мало дров, разве что на Буратино хватит. На самом деле материал очень распространенный и простой – вряд ли сложнее, чем то же скалярное произведение, даже типовых задач поменьше будет. Главное в аналитической геометрии, как многие убедятся или уже убедились, НЕ ОШИБАТЬСЯ В ВЫЧИСЛЕНИЯХ. Повторяйте как заклинание, и будет вам счастье =)
…Эти позитивные строки увидели свет много-много лет назад и вдохновили немало авторов. Но мало кто осознал, что моя дурь неповторима, поэтому читайте оригинал:D
Если векторы сверкают где-то далеко, как молнии на горизонте, не беда, начните с урока Векторы для чайников, чтобы восстановить или вновь приобрести базовые знания о векторах. Более подготовленным читателям – оглавление, я собрал самое нужное.
- Векторное произведение векторов
- Понятие и обозначение
- Определение векторного произведения, подробно, по пунктам, со смыслом.
- Векторное произведение коллинеарных векторов
- Свойства векторного произведения векторов, и, конечно, везде задачи.
- Векторное произведение векторов в координатах, через определитель.
- Смешанное произведение векторов
- Понятие и определение, опять же с комментариями.
- Смешанное произведение компланарных векторов
- Смешанное произведение векторов в координатах, некоторые свойства тут же.
Чем вас сразу порадовать? Векторное и смешанное произведение векторов определены и работают в трёхмерном пространстве, то есть «плоского» случая не будет. Уже проще!
Векторное произведение векторов
В данной операции, точно так же, как и в скалярном произведении, участвуют два вектора. Пусть это будут нетленные буквы ![]() .
.
Само действие обозначается следующим образом: ![]() . Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
. Существуют и другие варианты, но я привык обозначать векторное произведение векторов именно так, в квадратных скобках с крестиком.
И сразу вопрос: если в скалярном произведении векторов ![]() участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
участвуют два вектора, и здесь тоже умножаются два вектора, тогда в чём разница? Явная разница, прежде всего, в РЕЗУЛЬТАТЕ:
Результатом скалярного произведения векторов является ЧИСЛО: ![]()
Результатом векторного произведения векторов является ВЕКТОР: ![]() , то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву
, то есть умножаем векторы и получаем снова вектор. Закрытый клуб. Собственно, отсюда и название операции. В различной учебной литературе обозначения тоже могут варьироваться, я буду использовать букву ![]() .
.
Определение векторного произведения
Сначала будет определение с картинкой, затем комментарии.
Определение: векторным произведением ![]() неколлинеарных векторов
неколлинеарных векторов ![]() , взятых в данном порядке, называется ВЕКТОР
, взятых в данном порядке, называется ВЕКТОР ![]() , длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор
, длина которого численно равна площади параллелограмма, построенного на данных векторах; вектор ![]() ортогонален векторам
ортогонален векторам ![]() , и направлен так, что базис
, и направлен так, что базис ![]() имеет правую ориентацию:
имеет правую ориентацию:
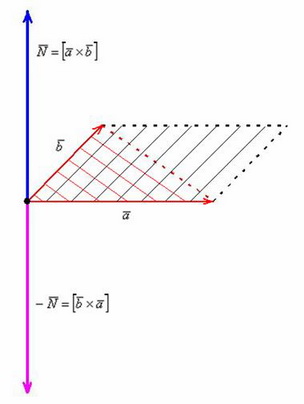
Разбираем определение по косточкам, тут много интересного!
Итак, можно выделить следующие существенные моменты:
1) Исходные векторы ![]() , обозначенные красными стрелками, по определению, не коллинеарны. Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
, обозначенные красными стрелками, по определению, не коллинеарны. Случай коллинеарных векторов будет уместно рассмотреть чуть позже.
2) Векторы ![]() взяты в строго определённом порядке:
взяты в строго определённом порядке: ![]() – «а» умножается на «бэ», а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР
– «а» умножается на «бэ», а не «бэ» на «а». Результатом умножения векторов является ВЕКТОР ![]() , который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор
, который обозначен синим цветом. Если векторы умножить в обратном порядке, то получим равный по длине и противоположный по направлению вектор ![]() (малиновый цвет). То есть справедливо равенство
(малиновый цвет). То есть справедливо равенство ![]() .
.
3) Теперь познакомимся с геометрическим смыслом векторного произведения. Это очень важный пункт! ДЛИНА синего вектора ![]() (а, значит, и малинового вектора
(а, значит, и малинового вектора ![]() ) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах
) численно равна ПЛОЩАДИ параллелограмма, построенного на векторах ![]() . На рисунке данный параллелограмм заштрихован чёрным цветом.
. На рисунке данный параллелограмм заштрихован чёрным цветом.
Примечание: чертёж является схематическим, и, естественно, номинальная длина векторного произведения не равна площади параллелограмма.
Вспоминаем одну из геометрических формул: площадь параллелограмма равна произведению смежных сторон на синус угла между ними. Поэтому, исходя из вышесказанного, справедлива формула вычисления ДЛИНЫ векторного произведения:
![]()
Подчёркиваю, что в формуле речь идёт о ДЛИНЕ вектора, а не о самом векторе ![]() . Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
. Каков практический смысл? А смысл таков, что в задачах аналитической геометрии площадь параллелограмма часто находят через понятие векторного произведения:
![]()
Получим вторую важную формулу. Диагональ параллелограмма (красный пунктир) делит его на два равных треугольника. Следовательно, площадь треугольника, построенного на векторах ![]() (красная штриховка), можно найти по формуле:
(красная штриховка), можно найти по формуле:
![]()
4) Не менее важный факт состоит в том, что вектор ![]() ортогонален векторам
ортогонален векторам ![]() , то есть
, то есть ![]() . Разумеется, противоположно направленный вектор
. Разумеется, противоположно направленный вектор ![]() (малиновая стрелка) тоже ортогонален исходным векторам
(малиновая стрелка) тоже ортогонален исходным векторам ![]() .
.
5) Вектор ![]() направлен так, что базис
направлен так, что базис ![]() имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости, и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки. Мысленно совместите указательный палец с вектором
имеет правую ориентацию. На уроке о переходе к новому базису я достаточно подробно рассказал об ориентации плоскости, и сейчас мы разберёмся, что такое ориентация пространства. Объяснять буду на пальцах вашей правой руки. Мысленно совместите указательный палец с вектором ![]() и средний палец с вектором
и средний палец с вектором ![]() . Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение
. Безымянный палец и мизинец прижмите к ладони. В результате большой палец – векторное произведение ![]() будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он).
будет смотреть вверх. Это и есть правоориентированный базис (на рисунке именно он).
Теперь совместите указательный палец левой руки с тем же вектором ![]() , а средний – с вектором
, а средний – с вектором ![]() . При этом большой палец будет неизбежно смотреть вниз – по направлению вектора
. При этом большой палец будет неизбежно смотреть вниз – по направлению вектора ![]() . Это левый или левоориентированный базис
. Это левый или левоориентированный базис ![]() .
.
Образно говоря, данные базисы «закручивают» или ориентируют пространство в разные стороны. И это понятие не следует считать чем-то надуманным или абстрактным – так, например, ориентацию пространства меняет самое обычное зеркало, и если «вытащить отражённый объект из зазеркалья», то его в общем случае не удастся совместить с «оригиналом». Кстати, поднесите к зеркалу три пальца и проанализируйте отражение ;-) Или просто попробуйте совместить «базисы» левой и правой руки, после чего станет понятно, что указательные и средние пальцы не совмещаются.
…Как всё-таки хорошо, что вы теперь знаете о право- и левоориентированных базисах, ибо страшнЫ высказывания некоторых лекторов о смене ориентации =)
Векторное произведение коллинеарных векторов
Определение подробно разобрано, осталось выяснить, что происходит, когда векторы ![]() коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы
коллинеарны. Если векторы коллинеарны, то их можно расположить на одной прямой и наш параллелограмм тоже «складывается» в одну прямую. Площадь такого, как говорят математики, вырожденного параллелограмма равна нулю. Это же следует и из формулы ![]() – синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
– синус нуля или 180-ти градусов равен нулю, а значит, и площадь нулевая
Таким образом, если ![]() , то
, то ![]() и
и ![]() . Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю.
. Обратите внимание, что само векторное произведение равно нулевому вектору, но на практике этим часто пренебрегают и пишут, что оно тоже равно нулю.
Частный случай – векторное произведение вектора на самого себя:
![]()
С помощью векторного произведения можно проверять коллинеарность трёхмерных векторов, и данную задачу среди прочих мы тоже разберём.
Для решения практических примеров может потребоваться тригонометрическая таблица, чтобы находить по ней значения синусов.
Ну что же, разжигаем огонь:
Пример 1
а) Найти длину векторного произведения векторов ![]() , если
, если ![]()
б) Найти площадь параллелограмма, построенного на векторах ![]() , если
, если ![]()
Решение: нет, это не опечатка, исходные данные в пунктах условия я намеренно сделал одинаковыми. Потому что оформление решений будет отличаться!
а) По условию требуется найти длину вектора (векторного произведения). По соответствующей формуле:
![]()
Ответ: ![]()
Коль скоро спрашивалось о длине, то в ответе указываем размерность – единицы.
б) По условию требуется найти площадь параллелограмма, построенного на векторах ![]() . Площадь данного параллелограмма численно равна длине векторного произведения:
. Площадь данного параллелограмма численно равна длине векторного произведения:
![]()
Ответ: ![]()
Обратите внимание, что в ответе о векторном произведении речи не идёт вообще, нас спрашивали о площади фигуры, соответственно, размерность – квадратные единицы.
Всегда смотрим, ЧТО требуется найти по условию, и, исходя из этого, формулируем чёткий ответ. Может показаться буквоедством, но буквоедов среди преподавателей хватает, и задание с хорошими шансами вернётся на доработку. Хотя это не особо натянутая придирка – если ответ некорректен, то складывается впечатление, что человек не разбирается в простых вещах и/или не вник в суть задания. Этот момент всегда нужно держать на контроле, решая любую задачу по высшей математике, да и по другим предметам тоже.
Куда подевалась большая буковка «эн»? В принципе, её можно было дополнительно прилепить в решение, но в целях сократить запись, я этого не сделал. Надеюсь, всем понятно, что ![]() и
и ![]() – это обозначение одного и того же.
– это обозначение одного и того же.
Популярный пример для самостоятельного решения:
Пример 2
Найти площадь треугольника, построенного на векторах ![]() , если
, если ![]()
Формула нахождения площади треугольника через векторное произведение дана в комментариях к определению. Решение и ответ в конце урока.
На практике задача действительно очень распространена, треугольниками вообще могут замучить.
Для решения других задач нам понадобятся:
Свойства векторного произведения векторов
Некоторые свойства векторного произведения мы уже рассмотрели, тем не менее, я их включу в данный список.
Для произвольных векторов ![]() и произвольного числа
и произвольного числа ![]() справедливы следующие свойства:
справедливы следующие свойства:
1) ![]() В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
В других источниках информации данный пункт обычно не выделяют в свойствах, но он очень важен в практическом плане. Поэтому пусть будет.
2) ![]() – свойство тоже разобрано выше, иногда его называют антикоммутативностью. Иными словами, порядок векторов имеет значение.
– свойство тоже разобрано выше, иногда его называют антикоммутативностью. Иными словами, порядок векторов имеет значение.
3) ![]() – сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
– сочетательные или ассоциативные законы векторного произведения. Константы безпроблемно выносятся за пределы векторного произведения. Действительно, чего им там делать?
4) ![]() – распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
– распределительные или дистрибутивные законы векторного произведения. С раскрытием скобок тоже нет проблем.
В качестве демонстрации рассмотрим коротенький пример:
Пример 3
Найти ![]() , если
, если ![]()
Решение: по условию снова требуется найти длину векторного произведения. Распишем нашу миниатюру:
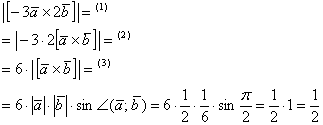
(1) Согласно ассоциативным законам, выносим константы за переделы векторного произведения.
(2) Выносим константу за пределы модуля, при этом модуль «съедает» знак «минус». Длина же не может быть отрицательной.
(3) Дальнейшее понятно.
Ответ: ![]()
Пора подбросить дров в огонь:
Пример 4
Вычислить площадь треугольника, построенного на векторах ![]() , если
, если ![]()
Решение: площадь треугольника найдём по формуле ![]() . Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов. Решение для ясности разобьём на три этапа:
. Загвоздка состоит в том, что векторы «цэ» и «дэ» сами представлены в виде сумм векторов. Алгоритм здесь стандартен и чем-то напоминает примеры № 3 и 4 урока Скалярное произведение векторов. Решение для ясности разобьём на три этапа:
1) На первом шаге выразим векторное произведение ![]() через векторное произведение
через векторное произведение ![]() , по сути, выразим вектор через вектор. О длинах пока ни слова!
, по сути, выразим вектор через вектор. О длинах пока ни слова!
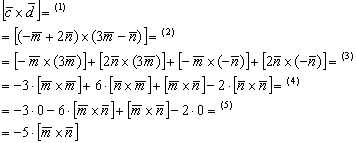
(1) Подставляем выражения векторов ![]() .
.
(2) Используя дистрибутивные законы, раскрываем скобки по правилу умножения многочленов.
(3) Используя ассоциативные законы, выносим все константы за пределы векторных произведений. При маломальском опыте действия 2 и 3 можно выполнять одновременно.
(4) Первое и последнее слагаемое равно нулю (нулевому вектору) благодаря приятному свойству ![]() . Во втором слагаемом используем свойство антикоммутативности векторного произведения:
. Во втором слагаемом используем свойство антикоммутативности векторного произведения: ![]()
(5) Приводим подобные слагаемые.
В результате вектор оказался выражен через вектор, чего и требовалось достичь:
![]()
2) На втором шаге найдем длину нужного нам векторного произведения. Данное действие напоминает Пример 3:
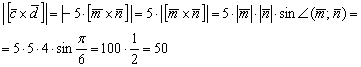
3) Найдём площадь искомого треугольника:
![]()
Этапы 2-3 решения можно было оформить и одной строкой.
Ответ: ![]()
Рассмотренная задача достаточно распространена в контрольных работах, вот пример для самостоятельного решения:
Пример 5
Найти ![]() , если
, если ![]()
Краткое решение и ответ в конце урока. Посмотрим, насколько вы были внимательны при изучении предыдущих примеров ;-)
Векторное произведение векторов в координатах
С векторами, заданными в координатах, всё тоже просто и прозрачно. Сразу обращаю внимание на то, что разговор пойдёт о координатах ортонормированного базиса. В общем случае аффинного базиса нижеприведённая формула будет нерабочей. Кстати, кто ещё не успел ознакомиться с базисами, рекомендую статью Линейная (не) зависимость векторов. Базис векторов.
Векторное произведение векторов ![]() , заданных в ортонормированном базисе
, заданных в ортонормированном базисе ![]() , выражается формулой:
, выражается формулой:
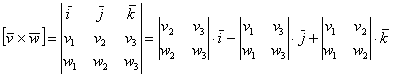
Формула и правда простецкая: в верхнюю строку определителя записываем координатные векторы, во вторую и третью строки «укладываем» координаты векторов ![]() , причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
, причём укладываем в строгом порядке – сначала координаты вектора «вэ», затем координаты вектора «дубль-вэ». Если векторы нужно умножить в другом порядке, то и строки следует поменять местами:
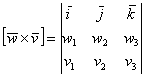
Согласно свойствам определителя, если в определителе две строки переставить местами, то он сменит знак. Этот факт полностью соответствует свойству антикоммутативности векторного произведения.
Данный определитель всегда раскрываем по первой строке, что продемонстрировано выше. Если есть трудности с определителями и формула не очень понятна, пожалуйста, посетите урок Как вычислить определитель, всё станет на свои места.
Что получается в результате раскрытия определителя?
В результате получается ВЕКТОР. А как иначе? Векторное произведение – это же вектор.
Пример 6
Найти векторное произведение векторов ![]() и его длину.
и его длину.
Решение: задача состоит из двух частей: во-первых, необходимо найти само векторное произведение (вектор), и во-вторых, его длину.
1) Найдём векторное произведение:
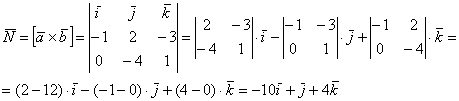
В результате получен вектор ![]() , или, ещё можно записать
, или, ещё можно записать ![]() .
.
Существует очень хороший способ проверки: как следует из определения, вектор ![]() должен быть ортогонален векторам
должен быть ортогонален векторам ![]() . Ортогональность векторов, как мы разбирались, проверяется с помощью скалярного произведения:
. Ортогональность векторов, как мы разбирались, проверяется с помощью скалярного произведения:
![]()
Если получилось хотя бы одно число, отличное от нуля, ищите ошибку в раскрытии определителя.
2) Вычислим длину векторного произведения. Используем простейшую формулу для вычисления длины вектора, которая рассматривалась на уроке Векторы для чайников:
![]()
Ответ: ![]()
В плане технических обозначений здесь, наоборот, вместо громоздкой конструкции ![]() выгодно использовать букву
выгодно использовать букву ![]() , поскольку она сокращает запись
, поскольку она сокращает запись
Аналогичный пример для самостоятельного решения:
Пример 7
Даны векторы ![]() . Найти
. Найти ![]() и вычислить
и вычислить ![]() .
.
Решение с ответом в конце урока. Будьте внимательны!
Огонь камина в самом разгаре, и самое время добавить живительный геометрический смысл в наши задачи:
Пример 8
Даны вершины треугольника ![]() . Найти его площадь.
. Найти его площадь.
Алгоритм решения, думаю, многие уже представляют. Сначала найдём векторы:
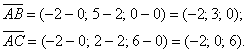
Затем векторное произведение:
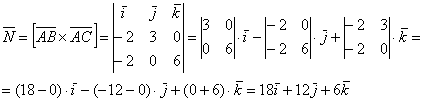
Вычислим его длину:
![]()
Формулы площадей параллелограмма и треугольника, само собой, остаются те же самые:
![]()
Ответ: ![]()
Рассмотренную задачу можно решить ещё двумя способами – было не обязательно выбирать стороны ![]() . Решение также допустимо провести через векторы
. Решение также допустимо провести через векторы ![]() либо
либо ![]() . Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. Настоятельно рекомендую выполнить схематический рисунок, чтобы лучше понять вышесказанное.
. Желающие могут проверить, что во всех трёх случаях получится один и тот же ответ. Настоятельно рекомендую выполнить схематический рисунок, чтобы лучше понять вышесказанное.
Еще одна важная особенность состоит в том, что в задачах на нахождение площади фигуры порядок векторов не имеет значения. Действительно, если находить ![]() , то получим противоположно направленный вектор
, то получим противоположно направленный вектор ![]() , но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Примерах № 6, 7, поскольку там требовалось найти вполне конкретный вектор.
, но формула вычисления длины вектора всё равно «съест» эти минусы. Заметьте, что такую перестановку нельзя делать в Примерах № 6, 7, поскольку там требовалось найти вполне конкретный вектор.
Пример 9
Вычислить площадь параллелограмма, построенного на векторах ![]() , если
, если ![]()
Это пример для самостоятельного решения.
В заключение первого раздела рассмотрим обещанную задачу урока Линейная (не) зависимость векторов. Базис векторов:
Пример 10
Проверить, будут ли коллинеарны следующие векторы пространства:
а) ![]()
б) ![]()
Решение: проверка основана на одном из утверждений данного урока: если векторы ![]() коллинеарны, то их векторное произведение равно нулю (нулевому вектору):
коллинеарны, то их векторное произведение равно нулю (нулевому вектору): ![]() .
.
а) Найдём векторное произведение:
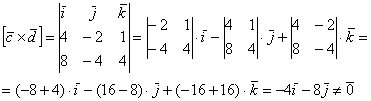
Таким образом, векторы ![]() не коллинеарны.
не коллинеарны.
б) Найдём векторное произведение:
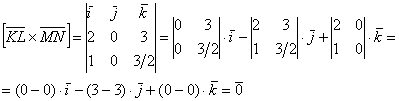
Значит, ![]()
Ответ: а) не коллинеарны, б) ![]()
Вот, пожалуй, и все основные сведения о векторном произведении векторов.
Смешанное произведение векторов
Данный раздел будет не очень большим, так как задач, где используется смешанное произведение векторов, немного. Фактически всё будет упираться в определение, геометрический смысл и пару рабочих формул.
Смешанное произведение векторов – это произведение трёх векторов:
![]()
Вот так вот они выстроились паровозиком и ждут, не дождутся, когда их вычислят.
Сначала опять определение и картинка.
Определение: смешанным произведением ![]() некомпланарных векторов
некомпланарных векторов ![]() , взятых в данном порядке, называется объём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис
, взятых в данном порядке, называется объём параллелепипеда, построенного на данных векторах, снабжённый знаком «+», если базис ![]() правый, и знаком «–», если базис
правый, и знаком «–», если базис ![]() левый.
левый.
Выполним рисунок. Невидимые нам линии прочерчены пунктиром:
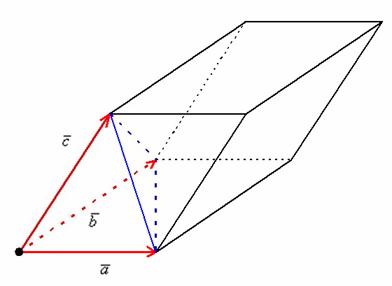
Погружаемся в определение:
1) Исходные векторы ![]() , обозначенные красными стрелками, не компланарны.
, обозначенные красными стрелками, не компланарны.
С компланарными векторами разберёмся ниже (что такое компланарность векторов, подробно разъяснено в статье Линейная (не) зависимость векторов. Базис векторов).
2) Векторы ![]() взяты в определённом порядке, то есть перестановка векторов в произведении
взяты в определённом порядке, то есть перестановка векторов в произведении ![]() , как вы догадываетесь, не проходит без последствий.
, как вы догадываетесь, не проходит без последствий.
3) Перед тем, как прокомментировать геометрический смысл, отмечу очевидный факт: смешанное произведение векторов является ЧИСЛОМ: ![]() . В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через
. В учебной литературе оформление может быть несколько другим, я привык обозначать смешанное произведение через ![]() , а результат вычислений буквой «пэ».
, а результат вычислений буквой «пэ».
По определению, смешанное произведение – это объем параллелепипеда, построенного на векторах ![]() (фигура прочерчена красными векторами и линиями чёрного цвета). То есть число
(фигура прочерчена красными векторами и линиями чёрного цвета). То есть число ![]() равно объему данного параллелепипеда.
равно объему данного параллелепипеда.
Примечание: чертёж является схематическим.
4) Не будем заново париться с понятием ориентации базиса и пространства. Смысл заключительной части состоит в том, что к объёму ![]() может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным:
может добавляться знак минус. Простыми словами, смешанное произведение может быть отрицательным: ![]() .
.
Непосредственно из определения следует формула вычисления объема параллелепипеда, построенного на векторах ![]() :
:
![]()
Знак модуля уничтожает возможный «минус» смешанного произведения.
В курсе аналитической геометрии доказано, что объём тетраэдра (на рисунке отсечён «синей» плоскостью) равен одной шестой объёма параллелепипеда:
![]()
В теории и практике тетраэдр часто называют треугольной пирамидой, поскольку все грани тетраэдра – треугольники.
Смешанное произведение компланарных векторов
Если векторы ![]() компланарны, то их можно расположить в одной плоскости. В результате параллелепипед «складывается» в плоскость, и объём такого вырожденного параллелепипеда равен нулю:
компланарны, то их можно расположить в одной плоскости. В результате параллелепипед «складывается» в плоскость, и объём такого вырожденного параллелепипеда равен нулю: ![]() .
.
Немного отвлекусь от темы, возможно, не все знают ответы на следующие вопросы:
– Чему равны длина и ширина точки?
– Чему равна площадь прямой?
– Чему равен объём плоскости?
С позиции геометрии ответ таков: нулю
Смешанное произведение векторов в координатах
Способ расчёта смешанного произведения векторов чисто алгебраический:
Смешанное произведение векторов ![]() , заданных в ортонормированном базисе
, заданных в ортонормированном базисе ![]() правой ориентации, выражается формулой:
правой ориентации, выражается формулой:
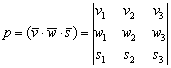
Определение, строго говоря, неполное, но в теоретические тонкости вникать не будем, правая ориентация базиса – это его «нормальная» ориентация, в которой мы будем решать практические задачи. Вполне достаточно.
В различных источниках на ваши головы выльют тонны различных свойств смешанного произведения. С практической точки зрения считаю важным отметить лишь некоторые вещи:
Как и для векторного произведения, координаты векторов следует «укладывать» в определитель в строгом порядке. Если в смешанном произведении ![]() выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.
выбрать два вектора (любых) и переставить их местами, то нужно переставить и соответствующие строки определителя. А по свойству определителя, при перестановке двух строк он меняет знак. Таким образом, при перестановке любых двух векторов смешанное произведение меняет знак.
Следует отметить, что координаты векторов не обязательно записывать в строки, их можно записать и в столбцы – слева направо, и тоже в строгом порядке:
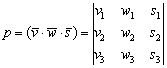
Значение определителя от этого не изменится (см. статью Свойства определителя и понижение его порядка). Дело вкуса.
Второй важный момент касается компланарности векторов. Как уже отмечалось, если векторы ![]() компланарны, то
компланарны, то 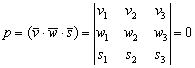
Такое задание уже было! В конце урока Линейная (не) зависимость векторов. Базис векторов мы разбирали задачу «доказать, что три вектора образуют базис пространства», где рассчитывали определитель третьего порядка и получали некоторое число. Так вот: по сути – мы находили смешанное произведение трёх векторов. И с геометрической точки зрения полученное число по модулю равнялось объёму параллелепипеда, построенного на данных векторах! Ну, а если получался ноль, то делали вывод, что векторы компланарны и базиса не образуют.
Закидываем остатки Буратино в огонь:
Пример 11
Даны векторы ![]() .
.
Вычислить:
а) смешанное произведение векторов;
б) объём параллелепипеда, построенного на векторах ![]() ;
;
в) объём тетраэдра, построенного на векторах ![]() .
.
Решение быстрое и простое:
а) По формуле смешанного произведения:
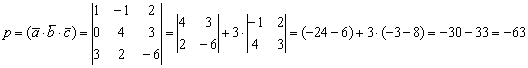
(Определитель раскрыт по первому столбцу)
б) Объём параллелепипеда, построенного на векторах ![]() , равен модулю смешанного произведения данных векторов:
, равен модулю смешанного произведения данных векторов:
![]()
в) Вычислим объём тетраэдра, построенного на данных векторах:
![]()
Ответ: ![]()
В пункте а) тоже можно было добавить размерность «кубические единицы», но здесь к объёму добавляется знак «минус», поэтому смотреться будет всё-таки не очень.
На практике, по моей субъективной оценке, в 95-99% случаев требуется вычислить объём треугольной пирамиды:
Пример 12
Вычислить объём треугольной пирамиды, если даны её вершины ![]()
Решение: чайникам рекомендую выполнить схематический рисунок пирамидки, чтобы лучше понять суть проводимых действий.
Сначала найдём векторы:
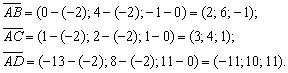
Вычислим смешанное произведение:
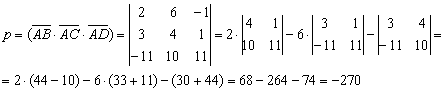
(Определитель раскрыт по первой строке)
Вычислим объём треугольной пирамиды ![]() :
:
![]()
Ответ: ![]()
Рассмотренная задача имеет не единственное решение, можно было взять и другую группу векторов, начиная движуху от любой другой вершины пирамиды. Чем-то похоже на задачу предыдущей части урока о площади треугольника.
Объём тетраэдра – хит смешанного произведения, поэтому заключительный счастливый номер пусть будет таким же:
Пример 13
Вычислить объём пирамиды, заданной вершинами ![]()
Это пример для самостоятельного решения. В образце решения рассмотрены векторы, отложенные от «традиционной» точки ![]() .
.
Остались только веселящие душу угольки, и в заключение хочу добавить, что в общем виде смешанное произведение векторов определено в аффинной системе координат. Более подробную информацию и формулы можно почерпнуть у тандема Атанасяна-Базылева.
Любите векторы, и векторы полюбят вас!
Решения и ответы:
Пример 2. Решение: по соответствующей формуле:
![]()
Ответ: ![]()
Пример 5. Решение:
1) Выразим вектор ![]() через вектор
через вектор ![]() :
:
![]()
2) Вычислим длину векторного произведения:
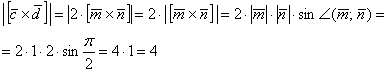
Ответ: ![]()
Пример 7. Решение: 1) Найдём векторное произведение:
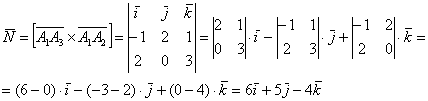
2) Вычислим длину векторного произведения:
![]()
Ответ: ![]()
Пример 9. Решение: найдём вектор:
![]() .
.
Векторное произведение:
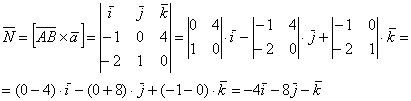
Площадь параллелограмма:
![]()
Ответ: ![]()
Пример 13. Решение: найдём векторы:
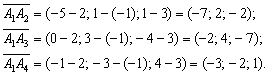
Вычислим смешанное произведение:
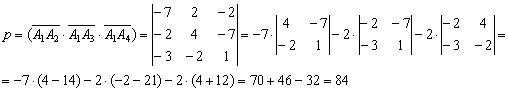
(Определитель раскрыт по первой строке)
Вычислим объём пирамиды ![]() :
:
![]()
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright