Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Как построить линию в полярной системе координат?

На предыдущем уроке мы познакомились с полярными координатами, а также научились строить отдельно взятые точки и распространённые кривые в данной системе координат. Давайте подведём краткие промежуточные итоги и ответим на важный вопрос:
как построить линию в полярной системе координат?

– Сначала необходимо отметить полюс, изобразить полярную ось и указать масштаб. Кроме того, на первоначальном этапе желательно найти область определения функции, чтобы сразу же исключить из рассмотрения лишние угловые значения.

– В большинстве случаев потребуется найти десяток-другой точек, принадлежащих линии. Но иногда можно обойтись меньшим количеством, а то и вовсе отделаться схематическим чертежом.

– На следующем шаге следует прочертить угловые направления и отметить найденные точки. Как это сделать с помощью каменного топора транспортира, циркуля и линейки, я подробнейшим образом объяснил в начале статьи о полярных координатах.

– И, наконец, отложенные точки нужно аккуратно-аккуратно соединить линией (линиями).

Отработаем алгоритм построения на более основательных типовых задачах:

Пример 6

Построить по точкам линию, заданную в полярной системе координат уравнением , рассматривая значения угла с интервалом в  рад. Найти уравнение линии в прямоугольной системе координат.

Решение: найдём область определения. Поскольку полярный радиус неотрицателен, то:

Очевидно, что условие выполнено для любого значения «фи», но, тем не менее, расскажу об удобном графическом способе решения тригонометрического неравенства: изобразите на черновике (или представьте мысленно) график функции  левой части неравеснтва и прямую  правой части неравенства. Непосредственно по чертежу видно, что синусоида расположена не ниже прямой , а значит, неравенство  выполнено для любого значения «икс».

Итак, на угол  не наложено никаких ограничений, и нам предстоит «перепахать» весь круг от 0 до , причём, по условию сделать это требуется строго с интервалом в  рад. (22,5 градусов). Ложку в зубы, калькулятор в руки:

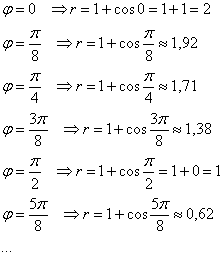
и так далее, пока не будет пройден весь оборот до «двух пи».

На практике обычно не расписывают подробные вычисления, а сразу заносят результаты в таблицу:

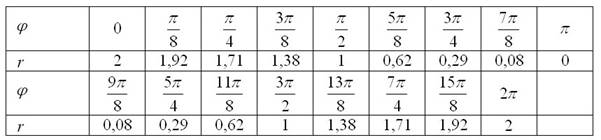
Рекомендую использовать мой расчётный макет, созданный в MS Excel, который позволит буквально в пару щелчков вычислить все значения «эр», сэкономив целый вагон времени. Программу можно раздобыть на странице Математические формулы и таблицы. Особо нетерпеливым читателям предлагаю также воспользоваться handmade-продуктом и быстро начертить заготовку, ориентируясь по клеточкам:

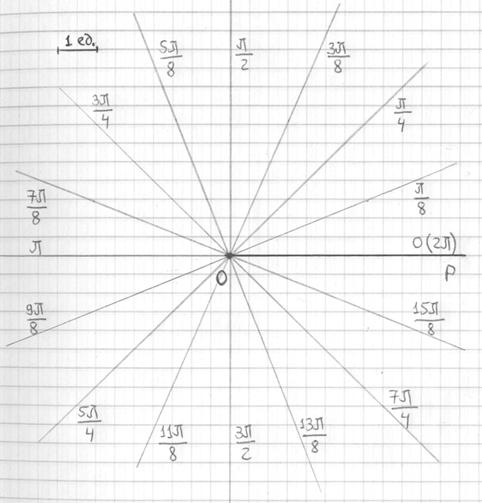
Углы проставлены для удобства и на чистовике, понятно, их записывать не надо.

…поймал себя на мысли, что уже добрые пару лет не выполнял чертежи от руки. Сейчас аккуратно извлеку тетрадь из сканера и спрячу её в укромном месте – лет через 20-30 продам на антикварном аукционе за 100500 золотых червонцев =) Шутки шутками, а оперативная память моего первого компьютера ZX Spectrum составляла 32 килобайта. КИЛОбайта. При этом программисты умудрялись затолкать туда аркадные игры с сотнями экранов и отличной графикой (по меркам 8-разрядных машин, конечно). Сейчас на дворе февраль 2014 года, а ведь с той поры не прошло и пары десятилетий. Боюсь, что шутливое сравнение чертёжных инструментов с каменным топором довольно скоро перестанет быть шуткой =)

После ностальгических воспоминаний отметим найденные точки на чертеже и аккуратно соединим их линией:

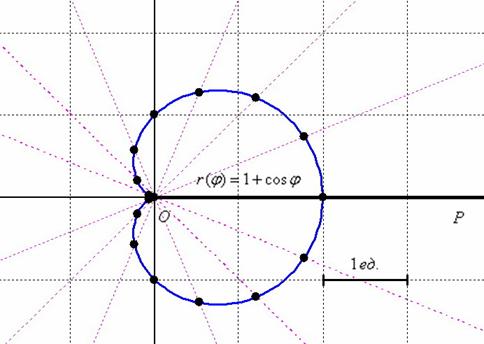
Напоминаю, что одинаковые значения радиуса эффективнее засекать циркулем, а слишком малые значения для углов   допустимо отметить и «на глазок».

Найдём уравнение линии в декартовой системе координат. Для этого используем тоже уже знакомый приём – домножим обе части уравнения  на «эр»:

И по формулам перехода к прямоугольным координатам  получим:

Перенесём «икс» налево и возведём обе части в квадрат:


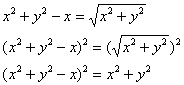
Дальнейшее возведение левой части в квадрат только усложнит запись, поэтому результат целесообразнее оставить в таком виде.

Из полученного уравнения следует, что кардиоида – это алгебраическая линия 4-го порядка, обратите внимание, насколько сложной получилась её формула по сравнению с полярной системой координат. Алгебраическим линиям 3-го, 4-го, 5-го, 6-го и высших порядков посвящены серьёзные исследования, и грибники без труда могут отыскать море информации по данной теме. Ну а я, как обычно, предлагаю вкусную и здоровую пищу на каждый день:

Пример 7

Линия задана уравнением  в полярной системе координат. Требуется:

1) построить линию по точкам, придавая  значения через интервал , начиная с  и заканчивая ;

2) найти уравнение линии в декартовой системе координат;

3) определить вид кривой.

Типовая формулировка, предвещающая час (а то и больше) усердного пыхтения, а нередко и чертыханья студента. Но только не того, кто прочитал эту и предыдущую статью о полярных координатах! Примерный образец оформления задачи в конце урока.

Рассмотрим ещё ряд важных особенностей решения:

Пример 8

Линия задана уравнением  в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от  до  и придавая  значения через промежуток ;

2) найти уравнение данной линии в прямоугольной системе координат;

3) назвать линию, найти координаты фокусов и эксцентриситет.

Решение: найдём область определения:

Заметьте, что ноль в знаменателе нас тоже не устраивает, поэтому неравенство становится строгим. Перенесём косинус направо и развернём избушку к лесу задом:

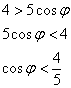
Неравенство несложно решить аналитически, но для лучшего понимания я опять воспользуюсь графическим методом. Изобразим на черновике или представим мысленно графики функций , при этом нас будет интересовать только один период – от   до . Условию  удовлетворяет та часть синусоиды, которая расположена ПОД прямой :

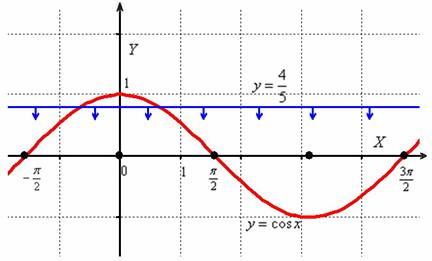
То есть, в нашем распоряжении оказываются почти все значения угла за исключением макушки, расположенной на симметричном отрезке .

Таким образом, . Арккосинус  составляет примерно 37 градусов, поэтому из рассмотрения исключаем углы  и . Заполним расчётную таблицу с прочерками в соответствующих ячейках:

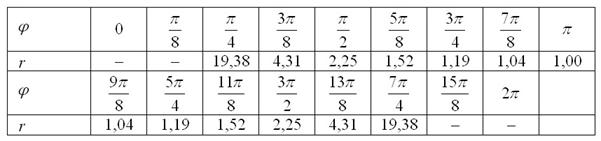
Чайники могут, в принципе, вообще не загружаться областью определения и ставить тире по факту: получилось отрицательное значение «эр» – поставили.

Выполним чертёж:

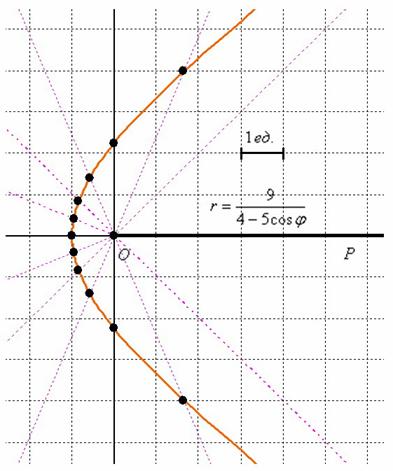
На него не вместились точки, соответствующие значениям , но не уменьшать же из-за этого масштаб. Сойдёт и так.

2) Найдём уравнение линии в прямоугольной системе координат. По всем признаком должна получиться гипербола.

Избавляемся от дроби:

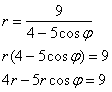
Используем формулы перехода :

Дальнейшие действия хорошо знакомы из практикума Задачи с линиями 2-го порядка:

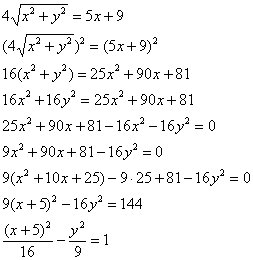
 – искомое уравнение.

3) Данная линия представляется собой гиперболу с центром в точке , действительной полуосью , мнимой полуосью . Впрочем, формально по условию можно было и не упоминать о деталях.

Вы спросите: «но в полярной же системе координат прорисовалась только одна ветвь гиперболы, поэтому не ошибочно ли говорить о целой гиперболе?». Не ошибочно!
И вот по какой причине: если подразумевать обобщённую полярную систему координат с отрицательными значениями «эр», то при значениях угла из интервала прорисуется левая ветвь! Желающие могут провести самостоятельную проверку и анализ этого факта. Я не сторонник и даже противник обобщенных полярных координат, но в данном случае всё получается ловко и чертовски удобно – можно как бы и не оговариваться о том, что на чертеже только одна ветвь гиперболы.

Вычислим координаты фокусов и эксцентриситет. По условию уравнение не нужно приводить к каноническому виду, а значит, требуемые вещи проще найти напрямую – с учётом параллельного переноса гиперболы, к тому же, она не повёрнута.

Вычислим значение  и поправкой на параллельный перенос в точку  найдём фокусы:

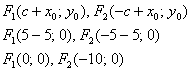
Эксцентриситет:

Готово.

Педантичные люди могут ещё записать развёрнутый ответ.

Заключительное задание для самостоятельного решения:

Пример 9

Линия задана уравнением  в полярной системе координат. Требуется:

1) построить линию по точкам, начиная от  до  и придавая  значения через промежуток ;

2) найти уравнение данной линии в прямоугольной системе координат и определить её вид.

3) Привести уравнение к каноническому виду и выполнить чертёж в прямоугольной системе координат. Найти фокусы кривой и её эксцентриситет.

Внимательно проанализируйте, что и в каком порядке требуется выполнить по условию. Сам много раз налетал – краем глаза показалось одно, а нужно совсем другое. В образце решения приведение уравнения линии 2-го порядка к каноническому виду выполнено академическим способом.

На основе полярных координат плоскости базируются цилиндрические и сферические координаты пространства. В частности, угловые величины широко используются в навигации (не зря упоминались лётчики и самолёты) и астрономии. Действительно, представьте земной шар (а если строго, эллипсоид), эллиптические орбиты планет и вы поймёте, что распиаренная прямоугольная система координат как-то здесь совсем не в тему. Ну а мне пора плотно прикрыть дверь аналитической геометрии и вернуться к матанализу, где полярные координаты тоже эксплуатируются на полную катушку.

До скорых встреч!

Решения и ответы:

Пример 7. Решение: 1) Найдём область определения функции:
 – любое.
Заполним таблицу требуемыми значениями угла и соответствующими значениями полярного радиуса:

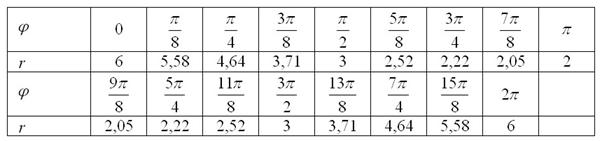
Выполним чертёж:

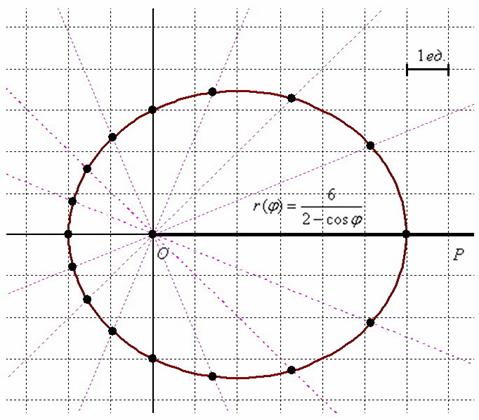
2)  Найдём уравнение линии в декартовой системе координат:

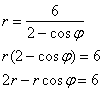
Используем формулы :

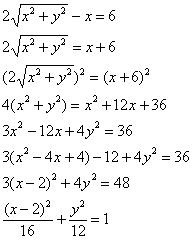
 – уравнение линии в прямоугольной системе координат.
3) Данная кривая представляет собой эллипс с центром симметрии в точке , большой полуосью  и малой полуосью .

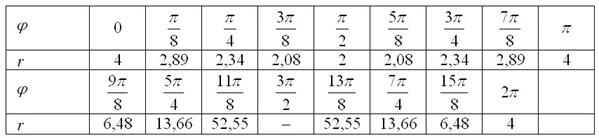
Пример 9. Решение: 1) Найдём область определения функции:

Заполним расчётную таблицу:

Выполним чертёж:

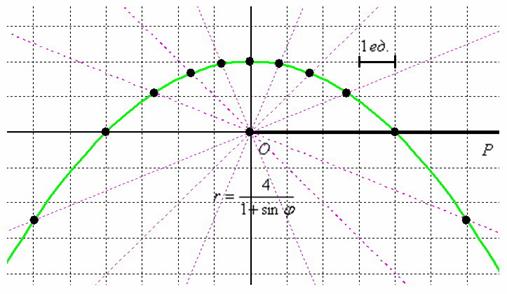
2)  Найдём уравнение линии в декартовой системе координат:

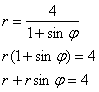
Используем формулы :

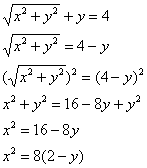
 – искомое уравнение. Это парабола.

3) Приведём уравнение линии к каноническому виду с помощью перехода к новой системе координат , которая получается путём поворота исходной системы координат  на  рад. вокруг точки  и её параллельным переносом центром в точку  (координаты – в старой системе координат).
В результате получено каноническое уравнение параболы , фокальный параметр которой равен . Выполним чертёж:

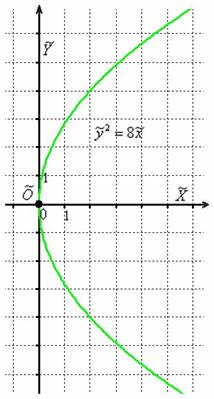
Найдём фокус: .
Эксцентриситет любой параболы равен единице.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте