


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Матричные уравнения. Примеры решений
Сейчас 00.12, 21 декабря 2012 года и я поздравляю всех посетителей сайта с Концом Света. Он оказался для меня самой настоящей находкой, поскольку каждый раз, начиная новую статью, я мучаюсь с первым абзацем, чтобы грамотно подобрать сухие точные фразы и сориентировать читателя в теме.
Тибетские монахи сказали, что Армагеддон будет продолжаться две недели (видимо, все были студентами и сдавали сессии), поэтому у чайников ещё есть время ознакомиться с уроками Действия с матрицами, Свойства матричных операций и матричные выражения, Как найти обратную матрицу? Это не так сложно и не так много, как кажется! То есть для освоения матричных уравнений необходимо обладать некоторыми навыками, и быть, если не шаманом матриц, то, по меньшей мере, матричным охотником. Не переживайте, Конец Концом, а матричные уравнения сдадутся на милость победителя.
Начнём с простого линейного уравнения, например уравнения ![]() . Оно состоит из математических знаков, чисел и неизвестной «икс». Перенесём «тройку» в правую часть и найдём решение уравнения:
. Оно состоит из математических знаков, чисел и неизвестной «икс». Перенесём «тройку» в правую часть и найдём решение уравнения:
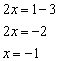
Выполним проверку, для этого подставим найденное значение ![]() в исходное уравнение:
в исходное уравнение:
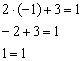
Получено верное равенство, значит, решение найдено правильно.
Про матричные уравнения рассказывать? =) Они устроены практически так же, только вместо чисел… правильно – матрицы (и конечно, числа тоже есть, помним, что матрицу можно умножить на число). Плюс особенные фишки, характерные для действий с матрицами. Всё просто, и особых трудностей возникнуть не должно.
Общие принципы решения матричных уравнений
Типовое матричное уравнение состоит, как правило, из нескольких матриц и неизвестной матрицы ![]() , которую предстоит найти. То есть, решением матричного уравнения является матрица.
, которую предстоит найти. То есть, решением матричного уравнения является матрица.
Пример 1
Решить матричное уравнение, выполнить проверку
![]()
Как решить матричное уравнение?
Фактически нужно использовать алгоритм решения детского уравнения с числами.
В правой части умножаем каждый элемент матрицы на три, а матрицу левой части переносим направо со сменой знака:
![]()
Причёсываем правую часть:
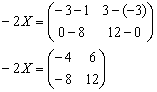
Выразим ![]() , для этого обе части уравнения умножим на
, для этого обе части уравнения умножим на ![]() :
:
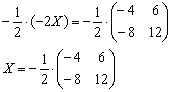
Все числа матрицы делятся на 2, поэтому уместно избавиться от дроби. А заодно и от «минуса». Делим каждый элемент матрицы на –2:
![]()
Ответ: ![]()
Как выполнить проверку?
Подставим найденное значение ![]() в левую часть исходного уравнения и проведём упрощения:
в левую часть исходного уравнения и проведём упрощения:
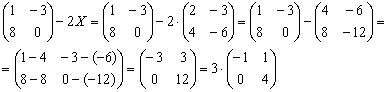
Последним действием вынесли «тройку» из матрицы.
Получена правая часть исходного уравнения, значит решение найдено правильно.
Кстати, всегда ли матричное уравнение вообще имеет решение? Конечно не всегда. С ходу привожу простейшее доказательство: ![]() .
.
Пример, который мы разобрали, элементарен, и, скажу честно, вероятность столкнуться с чем-то подобным на практике невелика. Поэтому перейдём к более содержательным заданиям, которые с вероятностью, стремящейся к 100%, встретятся вам в реальной контрольной работе. Но прежде систематизируем общий ход решения:
Распространённый алгоритм решения матричного уравнения
Итак, на голову упал стандартный персонаж, состоящий из нескольких матриц, некоторых множителей и птицы счастья ![]() .
.
На первом шаге уравнение приводится к одному из двух видов:
![]() либо
либо ![]() , где
, где ![]() – известные матрицы.
– известные матрицы.
Примечание: существует также третий вид: ![]() , но в действительности он встречается крайне редко. Тем не менее, в конце статьи я рассмотрю данный случай.
, но в действительности он встречается крайне редко. Тем не менее, в конце статьи я рассмотрю данный случай.
Как привести уравнение к виду ![]() или
или ![]() ? Все действия вы видели в Примере №1 – это перенос матриц из части в часть, «упаковывание» множителей в матрицы, матричное сложение/вычитание.
? Все действия вы видели в Примере №1 – это перенос матриц из части в часть, «упаковывание» множителей в матрицы, матричное сложение/вычитание.
На втором шаге нужно выразить ![]() или, выражаясь более академично, разрешить уравнение относительно
или, выражаясь более академично, разрешить уравнение относительно ![]() .
.
1) ![]() . Для того, чтобы разрешить данное уравнение относительно
. Для того, чтобы разрешить данное уравнение относительно ![]() , умножим обе его части на
, умножим обе его части на ![]() слева (здесь и далее предполагаем, что обратная матрица существует):
слева (здесь и далее предполагаем, что обратная матрица существует):
![]()
!!! Внимание! Произведение матриц не перестановочно, поэтому критически важно, с какой стороны проводить умножение.
По свойству матричных операций:![]() , поэтому:
, поэтому:
![]()
Единичную матрицу можно убрать (см. урок Свойства операций над матрицами. Матричные выражения):
![]()
Чего и требовалось достичь. Матрица ![]() нам не известна.
нам не известна.
2) ![]() . Умножаем обе части уравнения на
. Умножаем обе части уравнения на ![]() справа:
справа:
![]()
Согласно свойству матричных операций ![]() , получаем:
, получаем:
![]()
Единичную матрицу убираем:
![]()
Готово. Матрица ![]() нам опять же не известна.
нам опять же не известна.
Таким образом, на втором шаге решение выражается в виде ![]() либо в виде
либо в виде ![]() . Поскольку обратной матрицы мы не знаем, то третий этап решения будет состоять в её нахождении. Это стандартная задача урока Как найти обратную матрицу?
. Поскольку обратной матрицы мы не знаем, то третий этап решения будет состоять в её нахождении. Это стандартная задача урока Как найти обратную матрицу?
На заключительном четвёртом шаге выполняем матричное умножение ![]() или
или ![]() , и, собственно, получаем ответ.
, и, собственно, получаем ответ.
После выполнения задания желательно провести проверку, впрочем, в большинстве случаев её требуется выполнить по условию задачи. Схема обыденна – нужно подставить найденное значение ![]() в исходное уравнение и убедиться в том, что «всё сойдётся».
в исходное уравнение и убедиться в том, что «всё сойдётся».
Рассмотрим примеры решений уравнений обоих видов более подробно:
Решение матричного уравнения вида 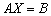
…и добавить нечего =)
Пример 2
Решить матричное уравнение, выполнить проверку
![]()
Решение: Уравнение уже имеет вид ![]() , поэтому никаких предварительных действий проводить не нужно.
, поэтому никаких предварительных действий проводить не нужно.
Для разрешения уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() слева:
слева:
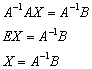
Да-да, прямо так и пишем при оформлении решения. Хотя можно ограничиться единственной фразой: «Решение ищем в виде ![]() » – без всяких пояснений и вывода формулы
» – без всяких пояснений и вывода формулы ![]() .
.
Из условия известны матрицы ![]() , однако, обратной матрицы
, однако, обратной матрицы ![]() мы не знаем. Придётся её найти:
мы не знаем. Придётся её найти:
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
![]()
![]() – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
![]() – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
![]() – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Таким образом, обратная матрица:
![]()
На финише проводим матричное умножение и получаем решение:
![]()
Ответ: ![]()
Проверка: Подставим найденное значение ![]() в левую часть исходного уравнения:
в левую часть исходного уравнения:
![]()
Получена правая часть исходного уравнения. Таким образом, решение найдено правильно.
Следующая задача весьма любопытна, и некоторые из вас сделают для себя неожиданное открытие:
Пример 3
Решить матричное уравнение и сделать проверку:
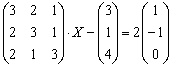
Решение: Неизвестная ![]() распложена справа от матрицы, и уравнение, очевидно, сведётся к виду
распложена справа от матрицы, и уравнение, очевидно, сведётся к виду ![]() . Используем уже знакомые из Примера №1 действия:
. Используем уже знакомые из Примера №1 действия:
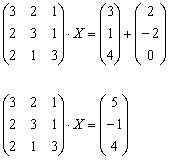
![]()
Для разрешения уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() слева:
слева:
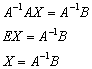
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
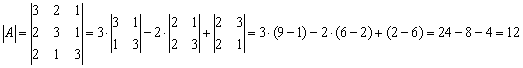
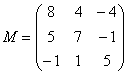 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
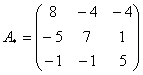 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
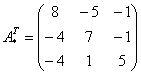 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Обратная матрица:
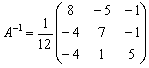
Таким образом, решение уравнения:
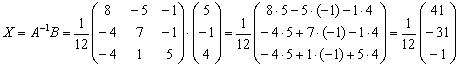
Ответ: 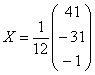
Дробь красивше оставить перед вектором-столбцом, хотя вполне приемлемо записать и так: 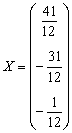 .
.
Проверка: Подставим найденное значение ![]() в левую часть исходного уравнения:
в левую часть исходного уравнения:
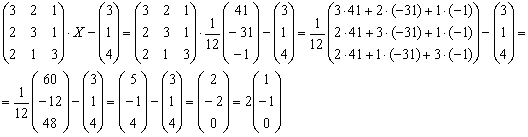
Получена правая часть исходного уравнения, таким образом, решение найдено верно.
Напоминаю технический приём, который мы рассмотрели на уроке Свойства операций над матрицами. Матричные выражения. После подстановки ![]() в левую часть уравнения, константа
в левую часть уравнения, константа ![]() уютно расположилась между матрицами. В подобных случаях число лучше вынести вперёд и разобраться с ним в самом конце – после матричного умножения.
уютно расположилась между матрицами. В подобных случаях число лучше вынести вперёд и разобраться с ним в самом конце – после матричного умножения.
А теперь остановимся вот на каком моменте…. Вернёмся к самому началу решения, когда мы получили матричное уравнение в виде 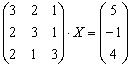 . Задача состояла в том, чтобы найти неизвестный вектор-столбец
. Задача состояла в том, чтобы найти неизвестный вектор-столбец 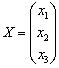 .
.
Перепишем уравнение в виде 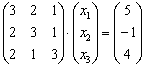 и в левой части умножим матрицы по обычному правилу:
и в левой части умножим матрицы по обычному правилу:
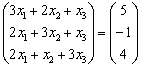
До боли знакомая картина =) Две матрицы равны, когда равны их соответствующие элементы. Это система трёх линейных уравнений с тремя неизвестными:
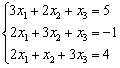
И полученный нами ответ 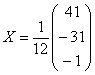 представляет собой решение данной системы:
представляет собой решение данной системы:
![]() .
.
Таким образом, матричный метод решения системы – это, по сути, частный случай матричного уравнения.
Пример 4
Найти ![]() из матричного уравнения:
из матричного уравнения:
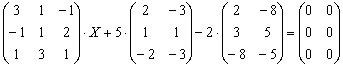
Проверить полученный результат.
Заметьте, что справа находится нулевая матрица а не ноль. Нулевая матрица для матриц – это аналог нуля для чисел. И её можно не записывать, после того, как вы что-нибудь перенесёте в правую часть.
Полное решение и примерный чистовой образец оформления задания в конце урока.
В процессе решения матричных уравнений у начинающих могут появиться трудности с умножением матриц. В этом случае, пожалуйста, вернитесь к матричным выражениям и отработайте данное действие.
Решение матричного уравнения вида 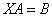
Алгоритм решения точно такой же с некоторыми содержательными и техническими отличиями:
Пример 5
Решить матричное уравнение, выполнить проверку найденного решения.
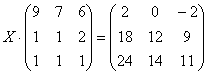
Решение: Уравнение имеет готовый вид ![]() , что позволяет сразу же заняться «иксом».
, что позволяет сразу же заняться «иксом».
Для разрешения уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() справа:
справа:
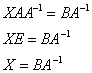
При оформлении можно записать и короче: «Решение ищем в виде ![]() ».
».
Матрица «бэ» известна. Берём матрицу 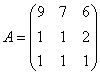 и без комментариев исследуем обратную сторону Луны:
и без комментариев исследуем обратную сторону Луны:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
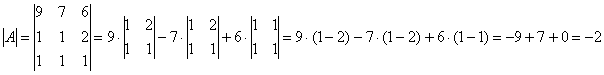
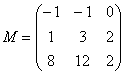 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
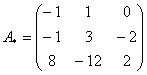 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
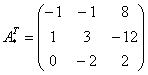 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Таким образом, обратная матрица:
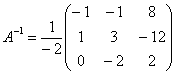
Находим решение, при этом не забываем про порядок умножения матриц, обратная матрица едет во втором вагоне:
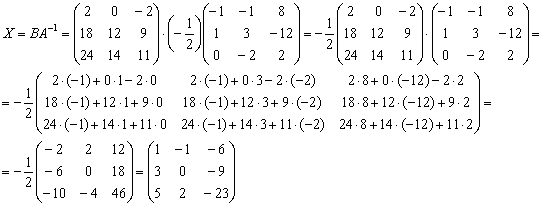
Ответ: 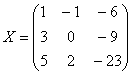
Проверка: Подставим найденное значение ![]() в левую часть исходного уравнения:
в левую часть исходного уравнения:
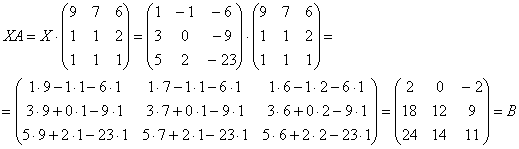
Получена правая часть исходного уравнения. Таким образом, решение найдено правильно.
Усложним задание:
Пример 6
Решить матричное уравнение, сделать проверку:
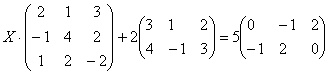
Решение: Незнакомец расположился слева от матрицы, поэтому уравнение сводится к виду ![]() . Упаковываем множители, переносим свободную матрицу в правую часть и выполняем вычитание матриц:
. Упаковываем множители, переносим свободную матрицу в правую часть и выполняем вычитание матриц:
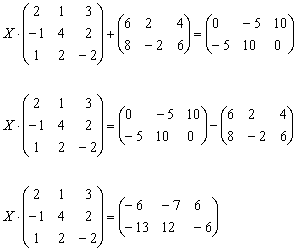
Для разрешения уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() справа:
справа:
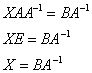
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
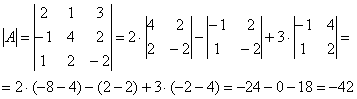
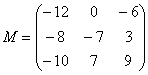 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
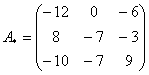 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
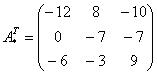 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Обратная матрица:
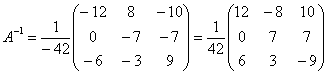
Здесь целесообразно внести минус в матрицу. Возможно, вам надоела однообразная картинка с нахождением обратной матрицы в каждом примере, я бы вполне мог пропускать данный пункт и сразу записывать: «обратная матрица такая-то…». Нет, полное решение приводится не случайно. Это отличная возможность потренироваться! Кроме того, у некоторых студентов действительно очень низкий уровень подготовки и полный трафарет того или иного примера будет как нельзя кстати. Да и сам Гугл, глядишь, научится решать матричные уравнения =)
Находим решение:
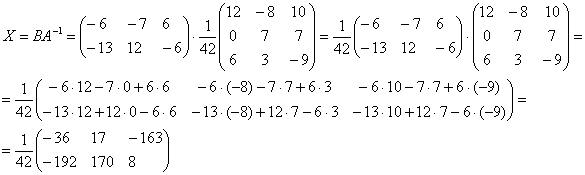
Ответ: ![]()
Проверка: Подставим найденное значение ![]() в левую часть исходного уравнения:
в левую часть исходного уравнения:
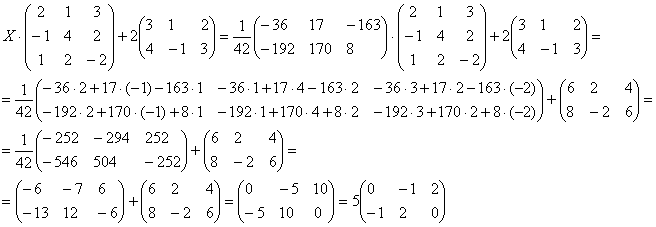
Получена правая часть исходного уравнения, таким образом, решение найдено верно.
Пример 7
Решить матричное уравнение и сделать проверку:
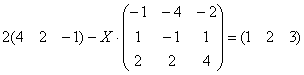
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
В заключение коротко рассмотрим ещё один тип матричного уравнения, который практически не встречается: ![]() , где
, где ![]() – известные матрицы. То есть, наш партизан залёг между двумя матрицами.
– известные матрицы. То есть, наш партизан залёг между двумя матрицами.
Разрешим данное уравнение относительно ![]() . Сначала умножим обе части на
. Сначала умножим обе части на ![]() слева:
слева:
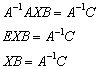
Теперь умножим обе части на ![]() справа:
справа:
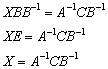
Готового примера у себя в коллекции я не нашёл, но сейчас всё равно что-нибудь подберу из этой оперы…. Вот:
![]()
Да, работёнки здесь побольше. Раза в два. Как решить данное уравнение?
– для матрицы ![]() находим обратную матрицу
находим обратную матрицу ![]() ;
;
– для матрицы ![]() находим обратную матрицу
находим обратную матрицу ![]() ;
;
– перемножаем три матрицы ![]() (см. статью про свойства матричных операций).
(см. статью про свойства матричных операций).
Желающие могут прорешать данный пример, верный ответ: ![]() .
.
Поздравляю ещё раз! Если вы читаете эти строки, то Конец Света так и не наступил! Конец Света как деньги – любит тишину =) На самом деле всё было так: летописцы майя составили свой календарь до дня зимнего солнцестояния 2012 года. А потом устали.
Но на всякий случай передаю привет следующей цивилизации. Когда-нибудь они откопают хорошо сохранившийся в вечной мерзлоте сервер и расшифруют нашу клинопись =)
Удачной сдачи зачётов и экзаменов!
Решения и ответы:
Пример 4: Решение: приведем уравнение к виду ![]() :
:
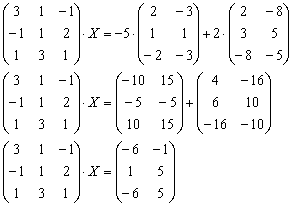
Для разрешения уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() слева:
слева:
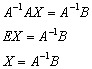
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
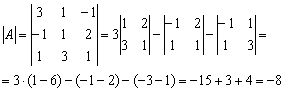
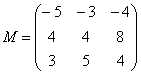 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
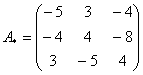 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
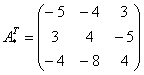 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Обратная матрица:
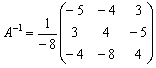
Решение уравнения:
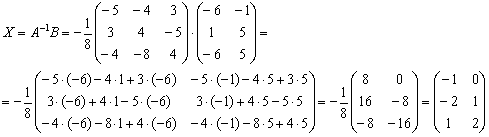
Ответ: 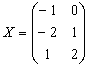
Проверка: подставим найденное значение ![]() в левую часть исходного уравнения:
в левую часть исходного уравнения:
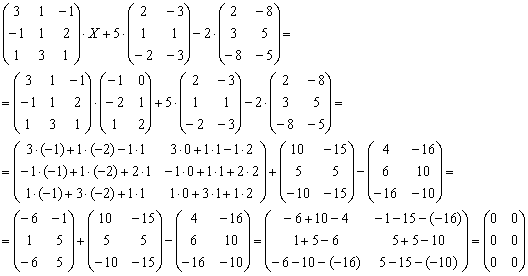
Получена правая часть исходного уравнения, таким образом, значение ![]() найдено верно.
найдено верно.
Пример 7: Решение: приведем уравнение к виду ![]() :
:
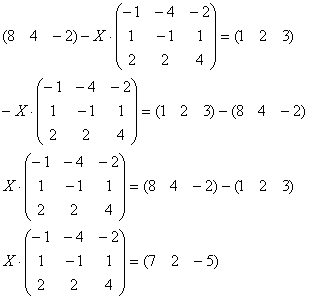
Для разрешения уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() справа:
справа:
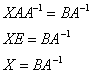
Обратную матрицу найдем по формуле:
![]() , где
, где ![]() – транспонированная матрица алгебраических дополнений соответствующих элементов матрицы
– транспонированная матрица алгебраических дополнений соответствующих элементов матрицы ![]() .
.
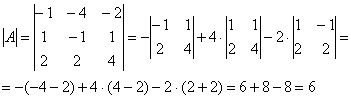
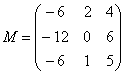 – матрица миноров соответствующих элементов матрицы
– матрица миноров соответствующих элементов матрицы ![]() .
.
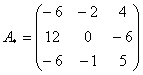 – матрица алгебраических дополнений.
– матрица алгебраических дополнений.
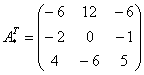 – транспонированная матрица алгебраических дополнений.
– транспонированная матрица алгебраических дополнений.
Обратная матрица: 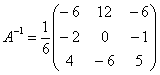
Таким образом:
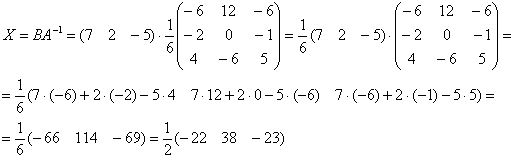
Ответ: ![]()
Проверка: подставим найденное значение ![]() в левую часть исходного уравнения:
в левую часть исходного уравнения:
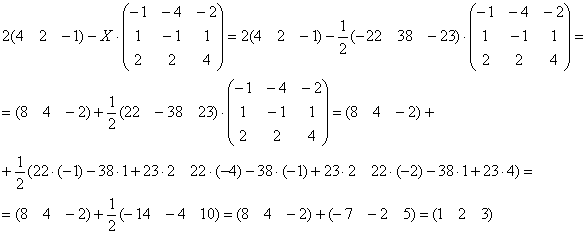
Получена правая часть исходного уравнения, таким образом, решение найдено верно.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright