Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

20. Уравнение линейной регрессии

На предыдущем уроке мы уже узнали, что такое линейная регрессия и научились находить её уравнение для несгруппированных данных (это когда даны две строчки или два столбца чисел). И сейчас тема получает продолжение – в данной статье я расскажу вам о том, как вычислить линейный коэффициент корреляции и как найти уравнение линейной регрессии в случае комбинационной группировки. Это когда в условии дана комбинационная таблица:

Пример 69

Имеются выборочные данные по 40 предприятиям региона:

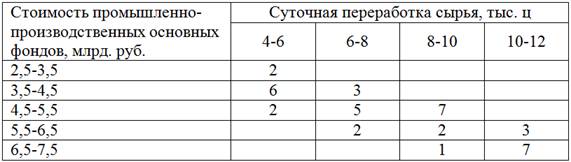
Требуется:

1) Определить признак-фактор  и признак-результат  и высказать предположение о наличии и направлении корреляционной зависимости  от . Построить корреляционное поле и выдвинуть гипотезу о возможной форме зависимости.

2) Вычислить линейный коэффициент корреляции и детерминации, сделать выводы.

3) Найти уравнение линейной регрессии  на  и изобразить соответствующую прямую на чертеже. Спрогнозировать среднюю суточную переработку сырья, когда стоимость основных фондов предприятий достигнет 9 млрд. руб.

Все термины и понятия вам уже знакомы! А если нет, то будут ссылки по ходу решения и, конечно же, видео – как это всё быстро подсчитать и нарисовать в Экселе + Калькулятор (сразу для особо страждущих).

1) Прежде всего в подобных задачах нам нужно обосновать причинно-следственную связь между признаками (если это не сделано в условии). Очевидно, что чем больше  стоимость основных фондов, тем крупнее предприятие и тем больше сырья оно способно переработать. Однако это не является непреложным правилом, ибо любое, самое крупное предприятие может неэффективно работать или даже простаивать. Тем не менее, общая тенденция состоит в том, что при увеличении стоимости фондов предприятий их средняя суточная переработка растёт. Такая нежёсткая зависимость называется… Правильно! Я приду к вам в вещих снах – будете вздрагивать и просыпаться от этой фразы :)

Таким образом, мы предполагаем наличие прямой корреляционной зависимости суточной переработки сырья (признак-результат) от стоимости основных фондов (фактор ).

Частоты комбинационной таблицы располагаются преимущественно по диагонали – от левого верхнего до правого нижнего угла, что подтверждает прямое направление зависимости («чем больше, тем больше»).

Теперь определим форму зависимости (линейная, квадратичная, экспоненциальная или какая-то другая). Простейший способ – графический, построили корреляционное поле и посмотрели. Для этого нужно немного модифицировать исходную таблицу, а именно перейти от интервальных вариационных рядов (левый столбец и 2-я сверху строка) к дискретным, выбрав в качестве вариант  и  середины соответствующих интервалов:

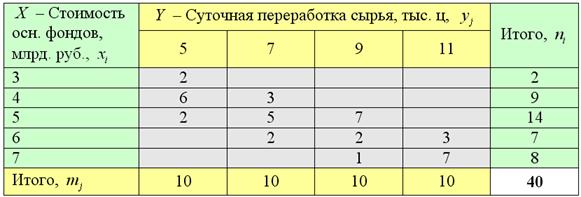
Заодно подсчитаем суммы частот по серым строкам (правый столбец) и суммы частот по серым столбцам (нижняя строка), не забыв убедиться в том, что итоговые суммы равны объёму выборки :

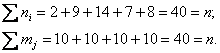
Довольно часто значения  и  уже подсчитаны и приведены в условии, но так бывает не во всех задачах, и поэтому я насыщаю решение всеми возможными действиями.

Обратите внимание, что значения  признака-фактора расположены по вертикали в левом столбце, а значения признака-результата – по горизонтали в «шапке» таблицы. Именно такое расположение (а не наоборот) чаще всего встречается на практике (ещё раз специально просмотрел с десяток методичек). Однако оно не сильно удобно в техническом плане, в частности, для построения корреляционного поля:

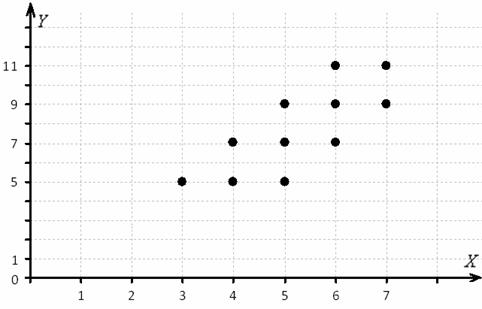
Ранее мы строили эмпирические линии регрессии – это простейший способ изобразить форму корреляционной зависимости. Однако гораздо удобнее привлечь на помощь функции. Анализируя чертёж, приходим к выводу, что эмпирические точки  «выстроились» примерно по прямой, что позволяет предположить наличие линейной корреляционной зависимости   – суточной переработки сырья от  – стоимости основных фондов.

Дальнейшие действия состоят в том, чтобы отыскать уравнение линейной регрессии , график которой проходит максимально близко к эмпирическим точкам (с учётом их «весов» – частот  в серых полях комбинационной таблицы), а также оценить тесноту линейной корреляционной зависимости – насколько близко расположены точки к построенной прямой. Эта теснота оценивается с помощью линейного коэффициента корреляции, с него и начнём:

2) Коэффициент корреляции вычислим по знакомой формуле .

Лично я привык в первую очередь находить средние  и стандартные отклонения . Эти расчёты мы проводили неоднократно.

Сначала разберёмся с признаком-фактором . Для этого из комбинационной таблицы (см. выше) выпишем значения  и заполним расчётную таблицу:

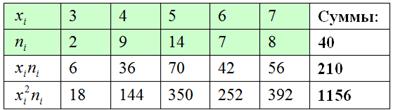
Вычислим среднее значение  млрд. руб. и среднее квадратическое отклонение, как корень из дисперсии, вычисленной по формуле:

Аналогично, берём игрековые значения из комбинационной таблицы и заполняем расчетную таблицу для признака-результата :

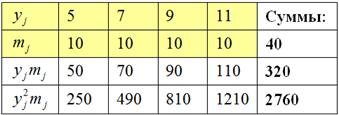
после чего рассчитываем нужные показатели:
 тыс. ц;

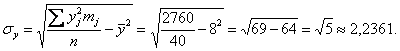
Теперь найдём среднее значение  произведения признаков. Для этого вычислим все возможные произведения  и  на соответствующие ненулевые частоты , наглядно распишу парочку штук:

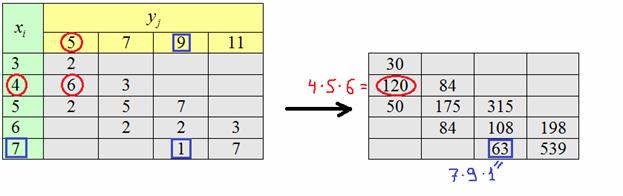
Вычислим сумму этих произведений:

и искомую среднюю:

Таким образом, линейный коэффициент корреляции:

В результате получено положительное число и, согласно шкале Чеддока, существует сильная прямая линейная корреляционная зависимость  суточной переработки сырья от  стоимости основных фондов.

Вычислим коэффициент детерминации:
, таким образом, в рамках построенной модели 69,12% вариации суточной переработки сырья обусловлено стоимостью основных фондов. Остальные  вариации обусловлено другими факторами.

В статье об индексе корреляции и детерминации я более подробно разберу построенную модель, и тогда последний вывод станет понятнее (для тех, кому он не очень понятен).

3) Найдём уравнение  линейной регрессии  на  (именно так на). Здесь можно использовать формулы предыдущего урока , но есть более академичный вариант. Искомое уравнение имеет вид:
, в данной задаче (вычисления приближённые):

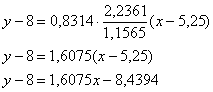
примерно:

Полученное уравнение показывает, что при увеличении стоимости основных фондов на 1 млрд. руб. суточная переработка сырья увеличивается в среднем на 1,61 тысяч центнеров.

Это очень важный вывод, который часто требуется в заданиях, по сути, смысл коэффициента «а».

Найдём пару удобных точек для построения графика:

отметим их на чертеже (красный цвет) и аккуратно проведём линию регрессии, её, как правило, изображают на том же чертеже:

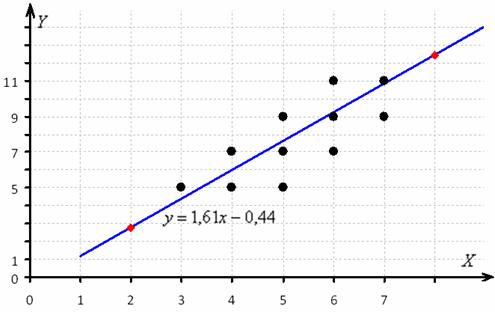
Спрогнозируем среднюю суточную переработку сырья при стоимости основных фондов в 9 млрд. руб.:
 тыс. ц.

Ещё раз подчёркиваю, что уравнение регрессии возвращает нам среднее, а точнее среднеожидаемое значение  признака-результата при различных значениях «икс» признака-фактора. И на самом деле уравнение регрессии корректнее записать так: , но дабы не разводить путаницу я использую максимально простые обозначения.

Теперь видео о том, как быстро расправиться с этой задачей:

 Как найти коэффициент корреляции и уравнение регрессии по таблице? (Ютуб), копия (Рутуб)

Для желающих сразу решить эту задачу есть калькулятор.

Готово.

Помимо рассмотренного, существует второе уравнение линейной регрессии –  на , его можно составить по формуле:
, после чего свести к виду:
 – полученное уравнение позволяет нам узнать средние значения «икс», соответствующие различным значениям «игрек»

Чисто формально эта регрессия существует всегда, так, в рассмотренной задаче признак  явно не зависит от , но вот линейная корреляционная зависимость есть! (причём, такой же тесноты). Помним, что причинно-следственная зависимость и корреляционная – это не одно и то же! Кроме того, в некоторых задачах признаки взаимно влияют друг на друга, уже известный вам пример:

 – количество произведённых куриц на птицефабрике;
 – количество произведённых яиц.

Здесь в уравнении регрессии  на  – самый что ни на есть здравый смысл.

График регрессии  тоже можно изобразить на чертеже, и примечателен тот факт, что он будет пересекать график  в точности в точке .

Следует добавить, что второе уравнение регрессии можно построить и для случая несгруппированных данных (см. задачи предыдущего урока о корреляции). Формула та же.

И я предлагаю вам потренироваться самостоятельно:

Пример 70

Известны следующие данные:

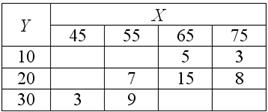
Найти линейный коэффициент корреляции и уравнения регрессии  на  и  на . Построить корреляционное поле, линии регрессии и определить их точку пересечения. Вычислить  и . По каждому пункту сделать выводы.

Обратите внимание, что в условии ничего не сказано о признаках , но нам ничего и не нужно о них знать, ведь задачу можно решить вне зависимости от того, где здесь признак-фактор, а где результат, и есть ли вообще причинно-следственная связь между признаками. Хотя, скорее всего, она здесь есть, ибо комбинационная группировка выполнена же из каких-то соображений.

Все числа уже в Экселе и вам остаётся выполнить вычисления; ничего страшного, если получится не очень красиво, важно наработать сам навык. Краткое решение для сверки чуть ниже.

И я вас поздравляю! – на этом «обязательная часть программы» завершена, надеюсь, корреляционно-регрессионный «минимум» освоен успешно.

Читатели с углублённым изучением статистики и просто энтузиасты непременно проверят значимость полученных результатов и затем мы разберём анатомию пАрной регрессии. Далее поговорим о нелинейной регрессии, ранговой корреляции Спирмена, коэффициенте корреляции Фехнера. И вишенка на торте, точнее, тыква на голове:))

Множественная корреляция и модель двухфакторной регрессии.

...И тыква таки материализовалась;) Снимайте маски и надевайте каски!

Решения и ответы:

Пример 70. Решение: вычислим частоты по каждому признаку:

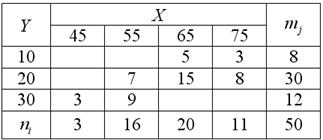
Линейный коэффициент корреляции найдём по формуле .
Заполним расчётную таблицу для признака :

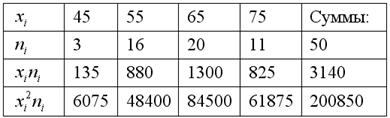
Вычислим среднее значение   и среднее квадратическое отклонение:

Заполним расчётную таблицу для признака :

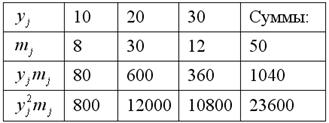
Вычислим  и
.

Вычислим произведения :

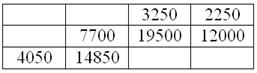
их сумму  и среднюю .

Вычислим линейный коэффициент корреляции:
, таким образом, существует заметная обратная линейная корреляционная зависимость между признаками (в обе стороны).

Составим уравнение линейной регрессии  на  (здесь и далее вычисления приближённые):

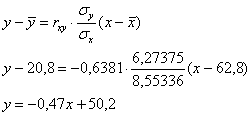
Полученное уравнение показывает, что при увеличении «икс» на 1 единицу «игрек» в среднем уменьшается примерно на 0,47 единицы.

Составим уравнение линейной регрессии  на :

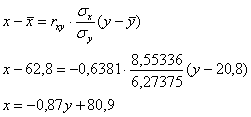
Полученное уравнение показывает, что при увеличении «игрек» на 1 единицу «икс» в среднем уменьшается примерно на 0,87 единицы.

Найдём точки для построения графиков:

построим корреляционное поле и изобразим линии регрессии:

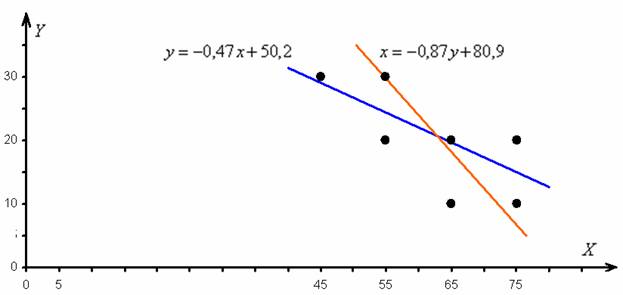
Линии регрессии пересекаются в точке

Вычислим:
 – среднеожидаемое значение «игрек» при ;
 – среднеожидаемое значение «икс» при  .

Примечание: вычисления местами не очень точные из-за округлений.

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте