7. Асимметрия и эксцесс эмпирического распределения

В предыдущих статьях мы познакомились с показателями центральной тенденции и вариации, и сейчас рассмотрим ещё пару характеристик статистической совокупности. Для тех, кто зашёл с поисковика и хочет изучить тему с азов, сразу ссылка на организационный урок: Математическая статистика для «чайников», там же, в конце, список всех статей курса. И до статьи 7-й – как рукой подать, после чего будет небольшой и очень приятый экзамен.

Итак, что такое асимметрия и эксцесс? Говоря простым языком, это показатели, характеризующие геометрическую форму распределения. Асимметрия характеризует меру скошенности графика влево / вправо, а эксцесс – меру его высоты.

Данные показатели рассчитываются как для эмпирических, так и для теоретических распределений, которые мы изучили в курсе теории вероятностей, и за «эталон» симметрии принято нормальное распределение:

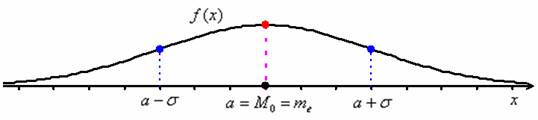
Очевидно, что любое нормальное распределение строго симметрично относительно своего центра, следовательно, его асимметрия равна нулю. Данный график кажется пологим, но стандартное отклонение в данном примере достаточно велико (см. на синие точки) и на самом деле такая высота «гармонична». Поэтому эксцесс нормального распределения (любого) принимают за «отправную» нулевую точку.

Почему именно нормальное распределение? Потому что философское – обязательно прочитайте эту интереснейшую статью по ссылке, если ещё не успели этого сделать!

В теории вероятностей существуют строгие формулы для вычисления коэффициентов асимметрии и эксцесса (будут ниже), но на практике мне такие задачи не встречались. И поэтому я сразу перехожу к статистике и распределениям эмпирическим, т.к. здесь таких задач как раз выше крыши. С положительным эксцессом, если выразиться тематически :)

Начнём с асимметрии. Асимметрия характеризует меру скошенности полигона или гистограммы влево / вправо относительно самого высокого участка, и во многих случаях для «прикидки» асимметрии достаточно взглянуть на соответствующие чертежи. Так, например, посмотрим на полигон частот из Примера 8:

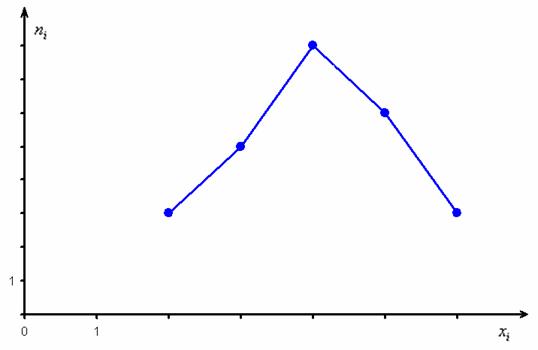
И, в принципе, тут всё видно – пациент скорее симметричен, чем асимметричен :)

Простейшим критерием симметрии является равенство средней, моды и медианы: но в жизни такого идеального совпадения, конечно, не бывает (даже тело человека немного асимметрично), и поэтому у «почти симметричных» распределений эти показатели должны располагаться очень близко друг к другу. И в самом деле, как мы вычислили в Примере 8: .

Обратите внимание, что рассматриваемые распределения имеют единственную модальную вершину, и далее речь пойдёт только о таких распределениях.

Правосторонняя асимметрия характеризуется удлинённым правым «хвостом», смотрим на гистограмму Примера 10:

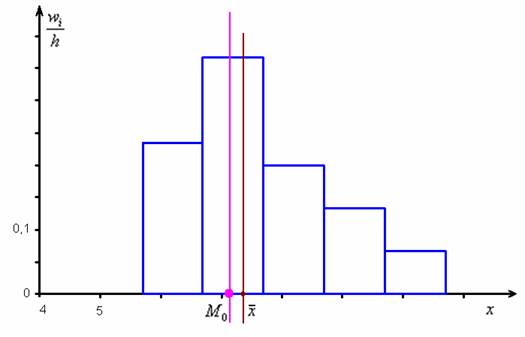
Простейшим признаком правосторонней асимметрии является тот факт, что , и это неудивительно – ведь справа находится значительное количество вариант, и поэтому средняя смещена вправо. И поэтому английский статистик Карл Пирсон, который ещё не раз нас порадует своими методами, предложил следующую формулу для расчёта коэффициента асимметрии:

, где – среднее квадратическое отклонение статистической совокупности. Что тоже логично, ведь у разных распределений – разный «разброс» значений и разные представления о мере асимметрии.

Левостороння асимметрия, наоборот, характеризуются удлинённым левый «хвостом» и неравенством ,…. картинки быстро не нашлось, поэтому просто разверну чертёж в графическом редакторе:

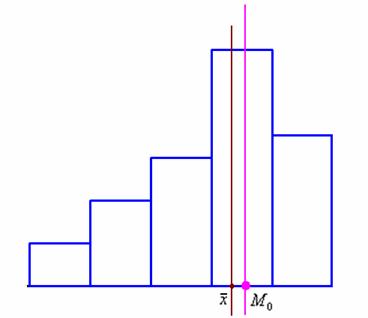
Из формулы следует, что в левостороннем случае коэффициент асимметрии отрицателен (т.к. ), а в правостороннем – положителен (), и чем больше по модулю – тем сильнее скос распределения.

Недостаток формулы Пирсона состоит в том, что она описывает лишь центральную часть распределения и практически не учитывает «периферию». И, чтобы вас не томить, сразу продвинутая формула, которая охватывает все варианты, для определённости запишу её для выборочной совокупности объёма :

, где – куб стандартного выборочного отклонения, а – так называемый центральный эмпирический момент третьего порядка. Для несгруппированной статической совокупности он рассчитывается так:
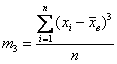( – выборочная средняя),
а для сформированного вариационного ряда – так:
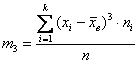, где – варианты дискретного ряда или середины частичных интервалов интервального ряда, а – соответствующие частоты.

Смысл знаков тот же самый: если , то распределение скошено вправо, если – то влево. При этом принята следующая условная градация: если полученное значение по модулю меньше, чем 0,25, то асимметрия незначительна, если , то умеренная, и если , то существенная.

И чем МЕНЬШЕ по модулю , тем рассматриваемое эмпирическое распределение БЛИЖЕ к нормальному распределению с параметрами .

Справочно формулы теории вероятностей: асимметрия случайной величины рассчитывается по «родственной» формуле , где – среднее квадратическое отклонение, а – центральный теоретический момент 3-го порядка. Для дискретной случайной величины он рассчитывается так: , а для непрерывной – через интеграл: .

Теперь об эксцессе замолвим слово. Он характеризует высоту и очень коварный. В том смысле, что глаза будут часто обманывать. Так, например, вернёмся к Примеру 7 статьи Интервальный вариационный ряд, единственное, я рассмотрю равные интервалы, как это на самом деле было в оригинальной задаче:

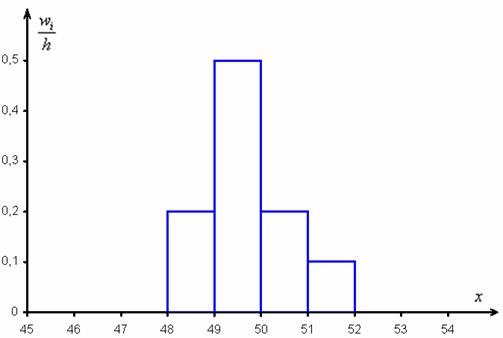
Ну видно же – гистограмма серьёзно вытянута вверх. Но это только кажется. Дело в том, что стандартное отклонение данной выборки невелико, и для сего небольшого рассеяния такая высота ДАЖЕ МАЛА. МалА – по сравнению с «эталонным» нормальным распределением с параметрами .

Поэтому аналитика и ещё раз аналитика. Коэффициент эксцесса эмпирического распределения рассчитывается по формуле:

, где – центральный эмпирический момент четвёртого порядка:
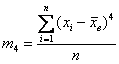– для несгруппированных данных, и
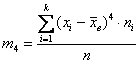– для сформированного вариационного ряда.

Для случайных величин из тервера формула схожа: , где – для дискретной, и – для непрерывной случайной величины.

Если , то эмпирическое распределение является более высоким («островершинным») – относительно «эталонного» нормального распределения с параметрами . Если же – то более низким и пологим. И чем больше по модулю, тем «аномальнее» высота в ту или иную сторону.

В примере выше, как ни странно, , и сейчас мы убедимся в этом аналитически:

Пример 19

Итак, сто пачек чая из Примера 7 ( – середины равных интервалов):

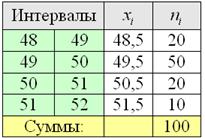
и нам требуется вычислить коэффициенты асимметрии и эксцесса

Решение: поскольку в формулах асимметрии и эксцесса фигурирует стандартное отклонение, то сначала нужно рассчитать выборочную среднюю и дисперсию.

Вычислим произведения , их сумму и грамм – средний вес пачки чая. Дисперсию здесь сподручнее найти не по формуле, а по определению: . Для этого рассчитаем произведения и сразу :

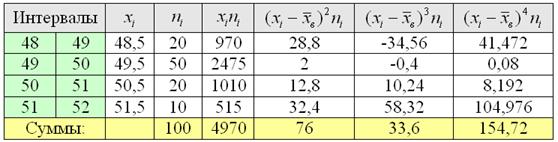
Ловкость рук и никаких трудностей, вы удивитесь, как всё быстро:

Если видео недоступно, смотрИте ролик здесь (Рутуб)

Собственно, финальные расчёты:

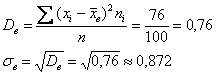
здесь правильнее, конечно, отклонение поправить, но обычно этим пренебрегают.

Центральные моменты 3-го и 4-го порядков:

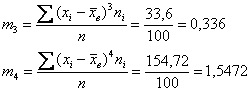
И, наконец, коэффициенты. Вычислим коэффициент асимметрии:
, то есть, распределение обладает существенной правосторонней асимметрией, что, кстати, хорошо было видно по чертежу.

Вычислим коэффициент эксцесса:
– вот оно как! Оказывается, распределение не то что выше, а заметно ниже, чем нормальное распределение с параметрами

Ответ:

Вот такой вот у нас получился эксекас :)

Помимо геометрических форм, эти коэффициенты позволяют «прикинуть», насколько близка к нормальному (или другому) распределению не только выборочная, но и вся генеральная совокупность. Это одна из важнейших задач статистики, которую мы разберём в разделе Статистические гипотезы.

Ну а сейчас я предлагаю вам небольшое экзаменационное задание по первым семи урокам. Оно типично для студенческой практики – дана статистическая совокупность, и требуется выполнить много-много чего. Внимательно проверьте, всё ли вы усвоили, всё ли умеете:

Пример 20

В результате эксперимента получены данные, записанные в виде статистического ряда:

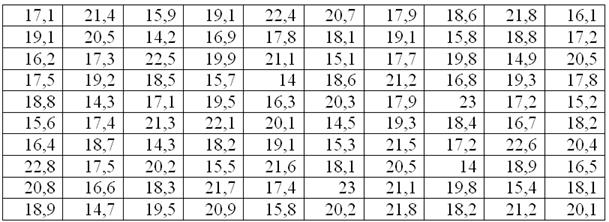
…это ещё ерунда :)

И сразу обратите внимание, что в условии речь идёт о результатах эксперимента, а значит, перед нами выборочная совокупность, т.к. теоретически опыты можно повторять бесконечное количество раз.

Задание 9

Выполнить в Экселе следующие действия (числа и макет уже там):

1) Составить интервальный вариационный ряд, состоящий из 9 равных интервалов. Видео в помощь.

2) Построить гистограмму относительных частот и эмпирическую функцию распределения.

3) Найти моду и медиану.

4) Вычислить выборочную среднюю, дисперсию, среднее квадратическое отклонение и коэффициент вариации.

5) Вычислить коэффициенты асимметрии и эксцесса, сделать выводы.

Не тушуйтесь – я с вами! Краткое решение для сверки внизу страницы.

И на этом, как вы правильно догадались, дело не заканчивается, поэтому сохраните файл с решением! Типовая задача содержит больше пунктов, и после изучения гипотезы о законе распределения генеральной совокупности, выполняем следующие задания:

6) По найденным характеристикам сделать вывод о форме эмпирического ряда распределения.

7) Построить нормальную кривую по опытным данным на графике гистограммы.

8) Произвести оценку степени близости теоретического распределения эмпирическому ряду с помощью критерия согласия Пирсона на уровне значимости 0,05.

Но о статистических гипотезах чуть позже. На следующем уроке речь пойдёт о статистических оценках и доверительных интервалах.

До скорых встреч!

Решения и ответы:

Пример 20. Решение:

1) По статистическим данным находим: , .
Вычислим размах вариации: ед.
По условию, выборку следует разделить на равных интервалов, таким образом, длина частичного интервала:
ед.
Разметим интервалы и подсчитаем частоты по каждому интервалу, после чего убедимся, что объём выборки . Вычислим относительные частоты и относительные накопленные частоты :

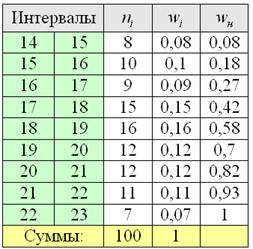
2) Построим гистограмму относительных частот. Поскольку длина частичного интервала , то плотности относительных частот совпадают с соответствующими частотами :

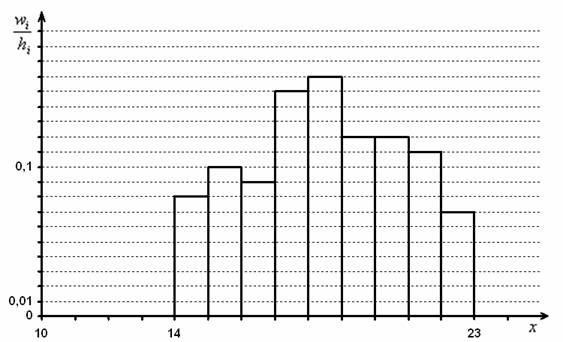
Построим эмпирическую функцию распределения:

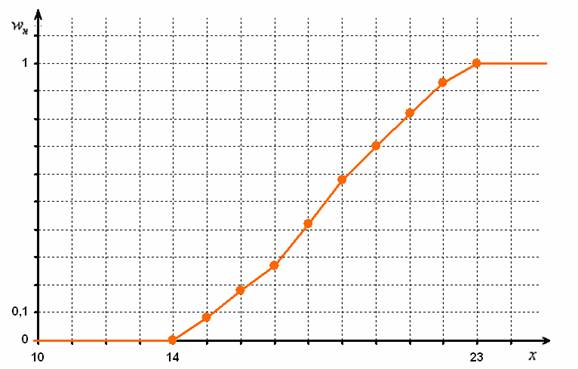
3) Моду вычислим по формуле , в данном случае:
– нижняя граница модального интервала;
– длина модального интервала;
– частота модального интервала;
– частота предыдущего интервала;
– частота следующего интервала.

Таким образом:
ед.

Медиану вычислим по формуле , в данном случае:
– объём выборочной совокупности;
половину вариант содержит интервал и – его нижняя граница;
– длина медианного интервала;
– частота медианного интервала;
– накопленная частота предыдущего интервала.

Таким образом:
ед.

4) Найдём середины интервалов, произведения и вычислим выборочную среднюю ед., после чего заполним оставшуюся часть таблицы и рассчитаем остальные показатели:

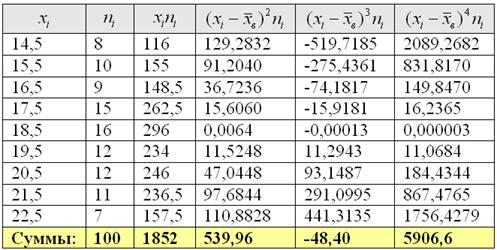
Выборочная дисперсия:
,
выборочное среднее квадратическое отклонение:
ед.,
коэффициент вариации:

5) Вычислим центральные эмпирические моменты 3-го и 4-го порядков:

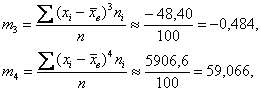
коэффициент асимметрии:

и коэффициент эксцесса:

Таким образом, выборочная совокупность практически симметрична, но несколько ниже, чем нормальное распределение с параметрами .

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?