


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Полярные координаты
Помимо аффинной системы координат и её популярного частного случая – прямоугольной (декартовой) системы, существуют и другие подходы к построению координатной сетки плоскости и пространства. В частности, широкое распространение получила полярная система координат, которая невероятно удобна для решения целого спектра практических задач. И через считанные минуты, не успевши опомниться, вы уже будете уверенно ориентироваться в полярных координатах!
Чтобы определить полярную систему координат на плоскости, достаточно зафиксировать начало координат ![]() и задать единичный координатный вектор
и задать единичный координатный вектор ![]() . Точка
. Точка ![]() называется полюсом, а луч
называется полюсом, а луч ![]() , сонаправленный с вектором
, сонаправленный с вектором ![]() – полярной осью. Графический шаблон – проще некуда, одна точка, один вектор, одна линия:
– полярной осью. Графический шаблон – проще некуда, одна точка, один вектор, одна линия:
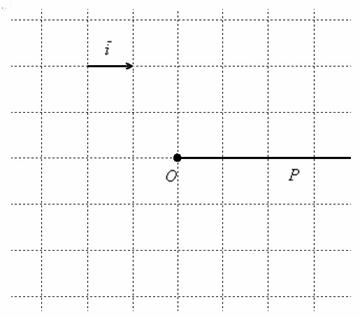
На практике вместо вектора можно где-нибудь в углу указать масштаб, например: 1 ед. = 1 см (две тетрадные клетки). По возможности, старайтесь выбирать именно такую, удобную во многих отношениях метрику.
А теперь сама мякотка:
Любая отличная от начала координат точка ![]() плоскости однозначно определяется своим расстоянием
плоскости однозначно определяется своим расстоянием ![]() от полюса и ориентированным углом
от полюса и ориентированным углом ![]() между полярной осью и отрезком
между полярной осью и отрезком ![]() :
:
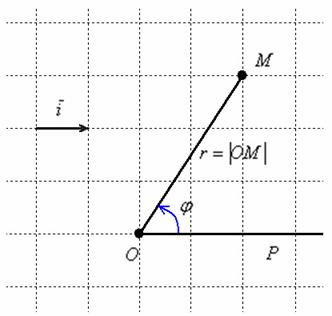
Для самого полюса ![]() , а угол
, а угол ![]() не определён. Не напоминает ли это вам кое-что из темы Комплексные числа? ;-)
не определён. Не напоминает ли это вам кое-что из темы Комплексные числа? ;-)
Число ![]() называют полярным радиусом точки
называют полярным радиусом точки ![]() или первой полярной координатой. Расстояние не может быть отрицательным, поэтому полярный радиус любой точки
или первой полярной координатой. Расстояние не может быть отрицательным, поэтому полярный радиус любой точки ![]() . Первую полярную координату также обозначают греческой буквой
. Первую полярную координату также обозначают греческой буквой ![]() («ро»), но я привык к латинскому варианту, и в дальнейшем буду использовать его.
(«ро»), но я привык к латинскому варианту, и в дальнейшем буду использовать его.
Число ![]() называют полярным углом данной точки или второй полярной координатой. Полярный угол стандартно изменяется в пределах
называют полярным углом данной точки или второй полярной координатой. Полярный угол стандартно изменяется в пределах ![]() (так называемые главные значения угла). Однако вполне допустимо использовать диапазон
(так называемые главные значения угла). Однако вполне допустимо использовать диапазон ![]() , а в некоторых случаях и вовсе возникает прямая необходимость рассмотреть все значения угла от нуля до «плюс бесконечности». Рекомендую, кстати, привыкнуть к радианной мере угла, поскольку оперировать градусами в высшей математике считается не комильфо.
, а в некоторых случаях и вовсе возникает прямая необходимость рассмотреть все значения угла от нуля до «плюс бесконечности». Рекомендую, кстати, привыкнуть к радианной мере угла, поскольку оперировать градусами в высшей математике считается не комильфо.
Пару ![]() называют полярными координатами точки
называют полярными координатами точки ![]() . Из
. Из ![]() легко найти и их конкретные значения. Тангенс острого угла прямоугольного треугольника – есть отношение противолежащего катета к прилежащему катету:
легко найти и их конкретные значения. Тангенс острого угла прямоугольного треугольника – есть отношение противолежащего катета к прилежащему катету: ![]() , следовательно, сам угол:
, следовательно, сам угол: ![]() . По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов:
. По теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов: ![]() , значит, полярный радиус:
, значит, полярный радиус: ![]()
Таким образом, ![]() .
.
Один пингвин хорошо, а стая – лучше ![]() :
:
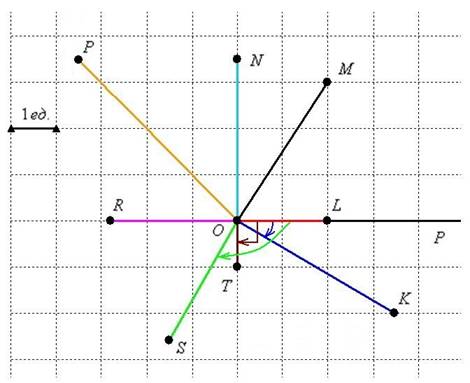
Отрицательно ориентированные углы ![]() я на всякий случай отметил стрелками, вдруг кто-то из читателей ещё не знал об этой ориентации. При желании можно «прикрутить» к каждому из них 1 оборот (
я на всякий случай отметил стрелками, вдруг кто-то из читателей ещё не знал об этой ориентации. При желании можно «прикрутить» к каждому из них 1 оборот (![]() рад. или 360 градусов) и получить, к слову, удобные табличные значения:
рад. или 360 градусов) и получить, к слову, удобные табличные значения:
![]()
Но недостаток этих «традиционно» ориентированных углов состоит в том, что они слишком далеко (более чем, на 180 градусов) «закручены» против часовой стрелки. Предчувствую вопрос: «почему недостаток и зачем вообще нужны какие-то отрицательные углы?» В математике ценятся самые короткие и рациональные пути. Ну а уж с точки зрения физики направление вращения зачастую имеет принципиальное значение – каждый из нас пытался открыть дверь, дёргая ручку не в ту сторону =)
Порядок и техника построения точек в полярных координатах
Красивые картинки красивы, однако построение в полярной системе координат – занятие достаточно кропотливое. Трудностей не возникает с точками, у которых полярные углы составляют ![]() , в нашем примере это точки
, в нашем примере это точки ![]() ; особых хлопот также не доставляют значения, кратные 45 градусам:
; особых хлопот также не доставляют значения, кратные 45 градусам: ![]() . Но как правильно и грамотно построить, скажем, точку
. Но как правильно и грамотно построить, скажем, точку ![]() ?
?
Потребуется клетчатый листок бумаги, карандаш и следующие чертёжные инструменты: линейка, циркуль, транспортир. В крайнем случае, можно обойтись одной линейкой, а то… и вовсе без неё! Читайте дальше и вы получите ещё одно доказательство, что эта страна непобедима =)
Пример 1
Построить точку ![]() в полярной системе координат.
в полярной системе координат.
Строим!
Прежде всего, нужно выяснить градусную меру угла ![]() . Если угол малознаком или вас есть сомнения, то всегда лучше воспользоваться таблицей либо общей формулой перевода радианов в градусы. Итак, наш угол составляет
. Если угол малознаком или вас есть сомнения, то всегда лучше воспользоваться таблицей либо общей формулой перевода радианов в градусы. Итак, наш угол составляет ![]() (или
(или ![]() ).
).
Начертим полярную систему координат (см. начало урока) и возьмём в руки транспортир. Обладателям круглого инструмента не составит труда отметить 240 градусов, но с большой вероятностью у вас на руках будет полукруглая версия девайса. Проблема полного отсутствия транспортира при наличии принтера и ножниц решается рукоделием.
Есть два пути: перевернуть листок и отметить 120 градусов, либо «прикрутить» пол оборота и рассмотреть противоположный угол ![]() . Выберем взрослый способ и сделаем отметку в 60 градусов:
. Выберем взрослый способ и сделаем отметку в 60 градусов:
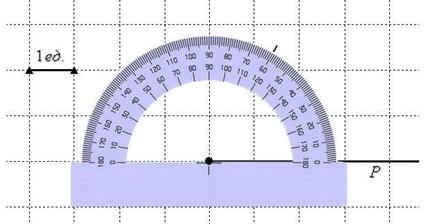
То ли транспортир лилипутский, то ли клетка гигантская =) Впрочем, чтобы отмерить угол масштаб не важен.
Проводим карандашом тонкую прямую, проходящую через полюс и сделанную отметку:
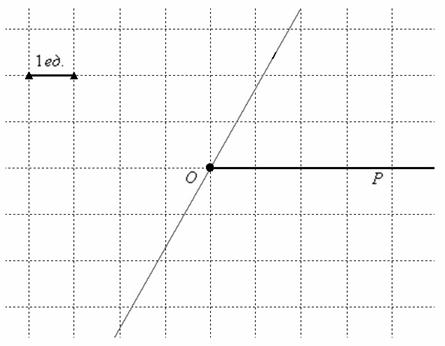
С углом разобрались, на очереди полярный радиус. Берём циркуль и по линейке устанавливаем его раствор в 3 единицы, чаще всего, это, конечно же, сантиметры:

Теперь аккуратно устанавливаем иглу на полюс, и вращательным движением выполняем небольшую засечку (красный цвет). Искомая точка ![]() построена:
построена:
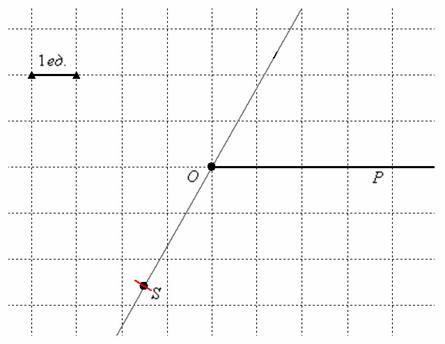
Можно обойтись без циркуля, приложив линейку непосредственно к построенной прямой и отмерив 3 сантиметра. Но, как мы увидим позже, в задачах на построение в полярной системе координат типична ситуация, когда нужно отметить две или бОльшее количество точек с одним и тем же полярным радиусом, поэтому эффективнее закалять металл. В частности, на нашем чертеже, развернув ногу циркуля на 180 градусов, легко сделать вторую засечку и построить симметричную относительно полюса точку ![]() . На ней давайте и отработаем материал следующего параграфа:
. На ней давайте и отработаем материал следующего параграфа:
Взаимосвязь прямоугольной и полярной системы координат
Очевидным образом присоединим к полярной системе координат «школьную» систему ![]() и изобразим на чертеже точку
и изобразим на чертеже точку ![]() :
:
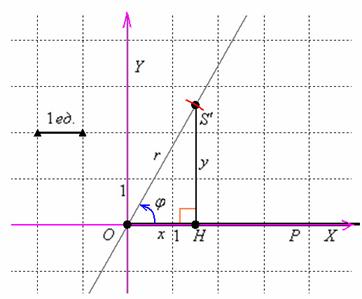
Такое присоединение всегда полезно держать в голове, когда выполняете чертёж в полярных координатах. Хотя, волей-неволей оно напрашивается и без лишнего намёка.
Установим взаимосвязь полярных ![]() и декартовых
и декартовых ![]() координат на примере конкретной точки
координат на примере конкретной точки ![]() . Рассмотрим прямоугольный треугольник
. Рассмотрим прямоугольный треугольник ![]() , в котором гипотенуза равна полярному радиусу:
, в котором гипотенуза равна полярному радиусу: ![]() , а катеты – «иксовой» и «игрековой» координатам точки
, а катеты – «иксовой» и «игрековой» координатам точки ![]() в декартовой системе координат:
в декартовой системе координат: ![]() .
.
Синус острого угла – есть отношение противолежащего катета к гипотенузе:
![]()
Косинус острого угла – есть отношение прилежащего катета к гипотенузе:
![]()
Заодно повторили определения синуса, косинуса (и чуть ранее тангенса) из программы 9 класса общеобразовательной школы.
Пожалуйста, занесите в свой справочник рабочие формулы ![]() , выражающие декартовы координаты точки через её полярные координаты – с ними нам придётся столкнуться ещё неоднократно, и в следующий раз прямо сейчас =)
, выражающие декартовы координаты точки через её полярные координаты – с ними нам придётся столкнуться ещё неоднократно, и в следующий раз прямо сейчас =)
Найдём координаты точки ![]() в прямоугольной системе координат:
в прямоугольной системе координат:
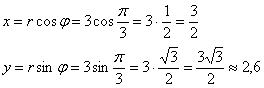
Таким образом: 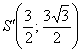
Полученные формулы открывают ещё одну лазейку в задаче построения, когда можно обойтись вообще без транспортира: сначала находим декартовы координаты точки (понятно, на черновике), затем мысленно находим нужное место на чертеже и отмечаем данную точку. На заключительном этапе проводим тонкую прямую, которая проходит через построенную точку и полюс. В результате получается, что угол якобы был отмерян транспортиром.
Забавно, что совсем отчаянные студенты, могут обойтись даже без линейки, используя вместо неё ровный край учебника, тетради или зачётной книжки – ведь о метрике позаботились производители тетрадей, 1 клетка = 5 миллиметров.
Напомнило мне всё это известный анекдот, в котором находчивые лётчики прокладывали курс по пачке Беломора =) Хотя, шутки шутками, а анекдот не так далёк от реальности, помнится, на одном из внутренних рейсов по РФ в лайнере отказали все навигационные приборы, и экипаж успешно посадил борт при помощи обычного стакана с водой, который показывал угол наклона самолёта относительно земли. А лётная полоса – вот она, из лобового стекла виднА.
Используя процитированную в начале урока теорему Пифагора, легко получить и обратные формулы: ![]() , следовательно:
, следовательно:
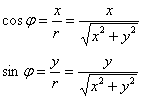
Сам угол «фи» стандартно выражается через арктангенс – абсолютно так же как и аргумент комплексного числа со всеми его заморочками.
Вторую группу формул также целесообразно поместить в свой справочный багаж.
После подробного разбора полётов с отдельно взятыми точками перейдём к закономерному продолжению темы:
Уравнение линии в полярных координатах
По существу, уравнение линии в полярной системе координат представляет собой функцию полярного радиуса ![]() от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от
от полярного угла (аргумента). При этом полярный угол учитывается в радианах (!) и непрерывно принимает значения от ![]() до
до ![]() (иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от
(иногда следует рассмотреть до бесконечности, или же в ряде задач для удобства от ![]() до
до ![]() ). Каждому значению угла «фи», которое входит в область определения функции
). Каждому значению угла «фи», которое входит в область определения функции ![]() , соответствует единственное значение полярного радиуса.
, соответствует единственное значение полярного радиуса.
Полярную функцию можно сравнить со своеобразным радаром – когда луч света, исходящий из полюса, вращается против часовой стрелки и «обнаруживает» (прорисовывает) линию.
Дежурным примером полярной кривой является Архимедова спираль ![]() . На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до
. На следующем рисунке изображен её первый виток – когда полярный радиус вслед за полярным углом принимает значения от 0 до ![]() :
:
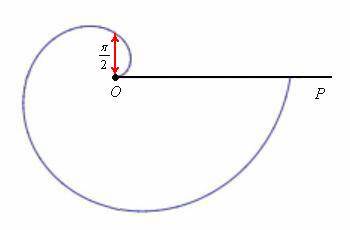
Далее, пересекая полярную ось в точке ![]() , спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне
, спираль продолжит раскручиваться, бесконечно далеко удаляясь от полюса. Но подобные случаи на практике встречаются довольно редко; более типичная ситуация, когда на всех последующих оборотах мы «пройдёмся по той же самой линии», которая получена в диапазоне ![]() .
.
В первом же примере мы сталкиваемся и с понятием области определения полярной функции: поскольку полярный радиус неотрицателен ![]() , то отрицательные углы здесь рассматривать нельзя.
, то отрицательные углы здесь рассматривать нельзя.
! Примечание: в ряде случаев принято использовать обобщённые полярные координаты, где радиус может быть отрицательным, и такой подход мы вкратце изучим чуть позже
Кроме спирали Архимеда, есть множество других известных кривых, но искусством, как говорится, сыт не будешь, поэтому я подобрал примеры, которые очень часто встречаются в реальных практических заданиях.
Сначала простейшие уравнения и простейшие линии:
Уравнение вида ![]() задаёт исходящий из полюса луч. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
задаёт исходящий из полюса луч. Действительно, вдумайтесь, если значение угла всегда (каким бы ни было «эр») постоянно, то какая это линия?
Примечание: в обобщённой полярной системе координат данное уравнение задаёт прямую, проходящую через полюс
Уравнение вида ![]() определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса
определяет… догадайтесь с первого раза – если для любого угла «фи» радиус остаётся постоянным? Фактически это определение окружности с центром в полюсе радиуса ![]() .
.
Например, ![]() . Для наглядности найдём уравнение данной линии в прямоугольной системе координат. Используя полученную в предыдущем параграфе формулу
. Для наглядности найдём уравнение данной линии в прямоугольной системе координат. Используя полученную в предыдущем параграфе формулу ![]() , проведём замену:
, проведём замену:
![]()
Возведём обе части в квадрат:
![]() – уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.
– уравнение окружности с центром в начале координат радиуса 2, что и требовалось проверить.
Со времён создания и релиза статьи о линейной зависимости и линейной независимости векторов я получил несколько писем от посетителей сайта, которые задавали вопрос в духе: «вот есть простая и удобная прямоугольная система координат, зачём нужен ещё какой-то косоугольный аффинный случай?». Ответ прост: математика стремится объять всё и вся! Кроме того, в той или иной ситуации немаловажно удобство – как видите, с окружностью значительно выгоднее работать именно в полярных координатах по причине предельной простоты уравнения ![]() .
.
А иногда математическая модель предвосхищает научные открытия. Так, в своё время ректор Казанского университета Н.И. Лобачевский строго доказал, через произвольную точку плоскости можно провести бесконечно много прямых, параллельных данной. В результате он был ошельмован всем научным миром, но… опровергнуть данный факт никто не смог. Только спустя доброе столетие астрономы выяснили, что свет в космосе распространяется по кривым траекториям, где и начинает работать неевклидова геометрия Лобачевского, формально разработанная им задолго до этого открытия. Предполагается, что это свойство самого пространства, кривизна которого нам незаметна ввиду малых (по астрономическим меркам) расстояний.
Рассмотрим более содержательные задачи на построение:
Пример 2
Построить линию ![]()
Решение: в первую очередь найдём область определения. Так как полярный радиус неотрицателен, то должно выполняться неравенство ![]() . Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот, я советую более быстрый и наглядный метод решения:
. Можно вспомнить школьные правила решения тригонометрических неравенств, но в простых случаях как этот, я советую более быстрый и наглядный метод решения:
Представьте график косинуса. Если он ещё не успел отложиться в памяти, то найдите его на странице Графики элементарных функций. О чём нам сообщает неравенство ![]() ? Оно сообщает нам о том, что график косинуса должен располагаться не ниже оси абсцисс. А это происходит на отрезке
? Оно сообщает нам о том, что график косинуса должен располагаться не ниже оси абсцисс. А это происходит на отрезке ![]() . И, соответственно, интервал
. И, соответственно, интервал ![]() не подходит.
не подходит.
Таким образом, область определения нашей функции: ![]() , то есть график
, то есть график ![]() расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).
расположен справа от полюса (по терминологии декартовой системы – в правой полуплоскости).
В полярных координатах часто бывает смутное представление о том, какую линию определяет то или иное уравнение, поэтому чтобы её построить, необходимо найти принадлежащие ей точки – и чем больше, тем лучше. Обычно ограничиваются десятком-другим (а то и меньшим количеством). Проще всего, конечно же, взять табличные значения угла. Для бОльшей ясности к отрицательным значениям я буду «прикручивать» один оборот:
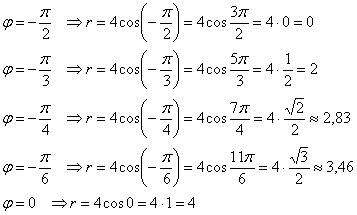
В силу чётности косинуса ![]() соответствующие положительные значения можно заново не считать:
соответствующие положительные значения можно заново не считать:
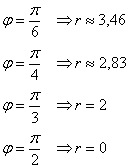
Изобразим полярную систему координат и отложим найденные точки, при этом одинаковые значения «эр» удобно откладывать за один раз, делая парные засечки циркулем по рассмотренной выше технологии:
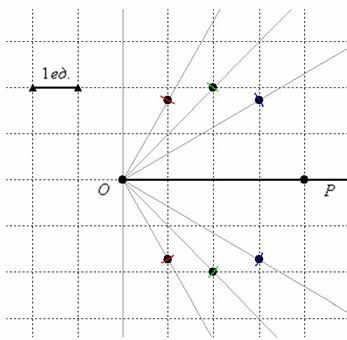
В принципе, линия отчётливо прорисовывается, но чтобы стопроцентно подтвердить догадку, давайте найдём её уравнение в декартовой системе координат. Можно применить недавно выведенные формулы ![]() , но я расскажу вам о более хитром приёме. Обе части уравнения
, но я расскажу вам о более хитром приёме. Обе части уравнения ![]() искусственно домножаем на «эр»:
искусственно домножаем на «эр»: ![]() и используем более компактные формулы перехода
и используем более компактные формулы перехода ![]() :
:
![]()
Выделяя полный квадрат, приводим уравнение линии к узнаваемому виду:
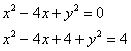
![]() – уравнение окружности с центром в точке
– уравнение окружности с центром в точке ![]() , радиуса 2.
, радиуса 2.
Коль скоро по условию требовалось просто выполнить построение и всё, плавно соединяем найденные точки линией:
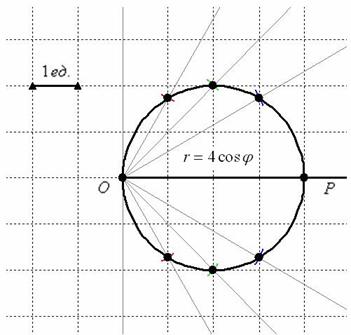
Готово. Ничего страшного, если получится немного неровно, вы же не обязаны были знать, что это окружность ;-)
Почему мы не рассмотрели значения угла вне промежутка ![]() ? Ответ прост: нет смысла. Ввиду периодичности функции
? Ответ прост: нет смысла. Ввиду периодичности функции ![]() нас ждёт бесконечный бег по построенной окружности.
нас ждёт бесконечный бег по построенной окружности.
Несложно провести нехитрый анализ и прийти к выводу, что уравнение вида ![]() задаёт окружность диаметра
задаёт окружность диаметра ![]() с центром в точке
с центром в точке ![]() . Образно говоря, все такие окружности «сидят» на полярной оси
. Образно говоря, все такие окружности «сидят» на полярной оси ![]() и обязательно проходят через полюс. Если же
и обязательно проходят через полюс. Если же ![]() , то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
, то весёлая компания перекочует налево – на продолжение полярной оси (подумайте, почему).
Похожая задача для самостоятельного решения:
Пример 3
Построить линию ![]() и найти её уравнение в прямоугольной системе координат.
и найти её уравнение в прямоугольной системе координат.
Систематизируем порядок решения задачи:
В первую очередь находим область определения функции, для этого удобно посмотреть на синусоиду, чтобы сразу же понять, где синус неотрицателен.
На втором шаге рассчитываем полярные координаты точек, используя табличные значения углов; проанализируйте, нельзя ли сократить количество вычислений?
На третьем шаге откладываем точки в полярной системе координат и аккуратно соединяем их линией.
И, наконец, находим уравнение линии в декартовой системе координат.
Примерный образец решения в конце урока.
Общий алгоритм и технику построения в полярных координатах мы детализируем
и существенно ускорим во второй части лекции, но перед этим познакомимся ещё с одной распространённой линией:
Полярная роза
Совершенно верно, речь пойдёт о цветке с лепестками:
Пример 4
Построить линии, заданные уравнениями в полярных координатах
а) ![]()
б) ![]()
Существует два подхода к построению полярной розы. Сначала пойдём по накатанной колее, считая, что полярный радиус не может быть отрицательным:
Решение:
а) Найдём область определения функции:
![]()
Такое тригонометрическое неравенство тоже нетрудно решить графически: из материалов статьи Геометрические преобразования графиков известно, что если аргумент функции удвоить, то её график сожмётся к оси ординат в 2 раза. Пожалуйста, найдите график функции ![]() в первом же примере указанного урока. Где данная синусоида находится выше оси абсцисс? На интервалах
в первом же примере указанного урока. Где данная синусоида находится выше оси абсцисс? На интервалах ![]() . Следовательно, неравенству
. Следовательно, неравенству ![]() удовлетворяют соответствующие отрезки, и область определения нашей функции:
удовлетворяют соответствующие отрезки, и область определения нашей функции: ![]() .
.
Вообще говоря, решение рассматриваемых неравенств представляет собой объединение бесконечного количества отрезков, но, повторюсь, нас интересует только один период.
Возможно, некоторым читателям более лёгким покажется аналитический способ нахождения области определения, условно назову его «нарезка круглого пирога». Резать будем на равные части и, прежде всего, найдём границы первого куска. Рассуждаем следующим образом: синус неотрицателен, когда его аргумент находится в пределах от 0 до ![]() рад. включительно. В нашем примере:
рад. включительно. В нашем примере: ![]() . Разделив все части двойного неравенства на 2, получаем искомый промежуток:
. Разделив все части двойного неравенства на 2, получаем искомый промежуток:
![]()
Теперь начинаем последовательно «нарезать равные куски по 90 градусов» против часовой стрелки:
– найденный отрезок ![]() , понятно, входит в область определения;
, понятно, входит в область определения;
– следующий интервал ![]() – не входит;
– не входит;
– следующий отрезок ![]() – входит;
– входит;
– и, наконец, интервал ![]() – не входит.
– не входит.
Прямо, как по ромашке – «любит, не любит, любит, не любит» =) С тем отличием, что тут не гадание. Да, прямо какая-то любовь по-китайски получается….
Итак, ![]() и линия
и линия ![]() представляет собой розу с двумя одинаковыми лепестками. Чертёж вполне допустимо выполнить схематически, однако крайне желательно правильно найти и отметить вершины лепестков. Вершинам соответствуют середины отрезков области определения, которые в данном примере имеют очевидные угловые координаты
представляет собой розу с двумя одинаковыми лепестками. Чертёж вполне допустимо выполнить схематически, однако крайне желательно правильно найти и отметить вершины лепестков. Вершинам соответствуют середины отрезков области определения, которые в данном примере имеют очевидные угловые координаты ![]() . При этом длины лепестков составляют:
. При этом длины лепестков составляют:
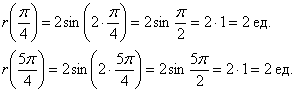
Вот закономерный результат заботливого садовника:
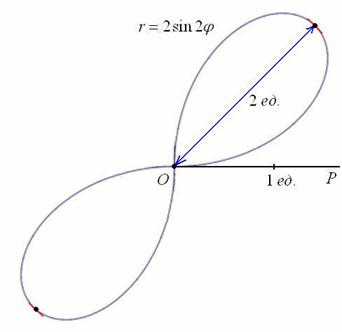
Следует отметить, что длину лепестка легко сразу усмотреть из уравнения ![]() – так как синус ограничен:
– так как синус ограничен: ![]() , то максимальное значение «эр» заведомо не превзойдёт двух.
, то максимальное значение «эр» заведомо не превзойдёт двух.
б) Построим линию, заданную уравнением ![]() . Очевидно, что длина лепестка этой розы тоже равна двум, но, прежде всего, нас интересует область определения. Применим аналитический метод «нарезки»: синус неотрицателен, когда его аргумент находится в пределах от нуля до «пи» включительно, в данном случае:
. Очевидно, что длина лепестка этой розы тоже равна двум, но, прежде всего, нас интересует область определения. Применим аналитический метод «нарезки»: синус неотрицателен, когда его аргумент находится в пределах от нуля до «пи» включительно, в данном случае: ![]() . Делим все части неравенства на 3 и получаем первый промежуток:
. Делим все части неравенства на 3 и получаем первый промежуток:
![]()
Далее начинаем «нарезку пирога кускам» по ![]() рад. (60 градусов):
рад. (60 градусов):
– отрезок ![]() войдёт в область определения;
войдёт в область определения;
– интервал ![]() – не войдёт;
– не войдёт;
– отрезок ![]() – войдёт;
– войдёт;
– интервал ![]() – не войдёт;
– не войдёт;
– отрезок ![]() – войдёт;
– войдёт;
– интервал ![]() – не войдёт.
– не войдёт.
Процесс успешно завершён на отметке 360 градусов.
Таким образом, область определения: ![]() .
.
Проводимые действия полностью либо частично несложно осуществлять и мысленно.
Построение. Если в предыдущем пункте всё благополучно обошлось прямыми углами и углами в 45 градусов, то здесь придётся немного повозиться. Найдём вершины лепестков. Их длина ![]() была видна с самого начала задания, осталось вычислить угловые координаты, которые равны серединам отрезков области определения:
была видна с самого начала задания, осталось вычислить угловые координаты, которые равны серединам отрезков области определения:
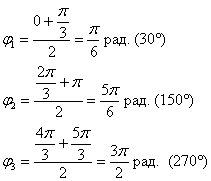
Обратите внимание, что между вершинами лепестков должны обязательно получиться равные промежутки, в данном случае 120 градусов.
Чертёж желательно разметить на 60-градусные секторы (отграничены зелёными линиями) и провести направления вершин лепестков (серые линии). Сами вершины удобно наметить с помощью циркуля – единожды отмерять расстояние в 2 единицы и нанести три засечки на прочерченных направлениях в 30, 150 и 270 градусов:
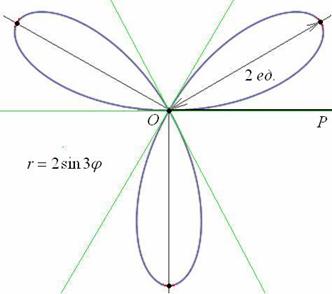
Готово. Понимаю, что занятие хлопотное, но если хотите всё оформить по уму, то придётся потратить время.
Сформулируем общую формулу: уравнение вида ![]() ,
, ![]() – натуральное число), задаёт полярную
– натуральное число), задаёт полярную ![]() -лепестковую розу, длина лепестка которой равна
-лепестковую розу, длина лепестка которой равна ![]() .
.
Например, уравнение ![]() задаёт четырёхлистник с длиной лепестка в 5 единиц, уравнение
задаёт четырёхлистник с длиной лепестка в 5 единиц, уравнение ![]() – 5-лепестковую розу с длиной лепестка в 3 ед. и т. д.
– 5-лепестковую розу с длиной лепестка в 3 ед. и т. д.
О втором подходе я хотел вообще умолчать, однако не могу пройти мимо – уж слишком он распространён. Суть состоит в том, что полярная роза часто рассматривается в обобщённых полярных координатах, где полярный радиус может быть отрицательным. Вопрос области определения отпадает, но появляются другие приколы.
Во-первых, разберёмся, как строить точки с отрицательным значением «эр». Если ![]() , то нужно мысленно найти точку с таким же углом, но радиуса
, то нужно мысленно найти точку с таким же углом, но радиуса ![]() и отобразить её симметрично относительно полюса. Вернёмся к первой полярной розе
и отобразить её симметрично относительно полюса. Вернёмся к первой полярной розе ![]() и рассмотрим интервал
и рассмотрим интервал ![]() , на котором полярный радиус отрицателен. Как, например, изобразить точку
, на котором полярный радиус отрицателен. Как, например, изобразить точку ![]() ? Мысленно находим точку
? Мысленно находим точку ![]() (левый верхний сектор) и отображаем её симметрично относительно полюса в точку
(левый верхний сектор) и отображаем её симметрично относительно полюса в точку ![]() . Таким образом, когда угол принимает значения из интервала
. Таким образом, когда угол принимает значения из интервала ![]() , то прорисовывается ещё один лепесток в правом нижнем секторе:
, то прорисовывается ещё один лепесток в правом нижнем секторе:
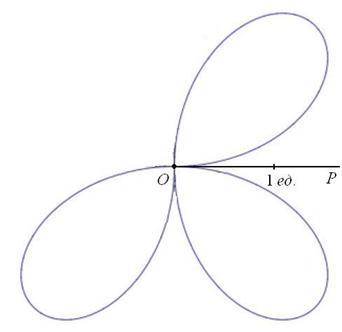
И, соответственно, когда угол проходит значения ![]() , то прорисовывается 4-й лепесток в противоположном (левом верхнем) секторе:
, то прорисовывается 4-й лепесток в противоположном (левом верхнем) секторе:
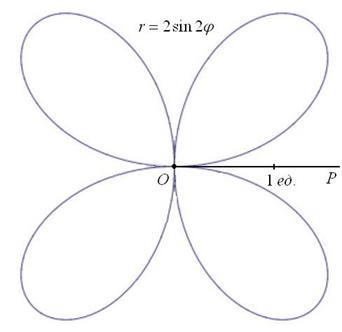
Интересно отметить, что при таком подходе вторая полярная роза ![]() сохраняет своё количество лепестков. А происходит это по одной простой причине: когда угол проходит пустующие секторы (ещё раз посмотрите на чертёж!), то полярный радиус принимает отрицательные значения и из этих пустых секторов точки отображаются напротив, ровнёхонько накладываясь на «легальные» лепестки.
сохраняет своё количество лепестков. А происходит это по одной простой причине: когда угол проходит пустующие секторы (ещё раз посмотрите на чертёж!), то полярный радиус принимает отрицательные значения и из этих пустых секторов точки отображаются напротив, ровнёхонько накладываясь на «легальные» лепестки.
Сформулируем правило розы для обобщенной системы координат: уравнение вида ![]() ,
, ![]() – натуральное) задаёт полярную розу с длиной лепестка
– натуральное) задаёт полярную розу с длиной лепестка ![]() , при этом:
, при этом:
1) если ![]() - чётное, то роза имеет ровно
- чётное, то роза имеет ровно ![]() лепестков;
лепестков;
2) если ![]() - нечётное, то роза имеет ровно
- нечётное, то роза имеет ровно ![]() лепестков.
лепестков.
Например, роза ![]() имеет 8 лепестков, роза
имеет 8 лепестков, роза ![]() – пять лепестков, роза
– пять лепестков, роза ![]() – 12 лепестков, роза
– 12 лепестков, роза ![]() – 7 лепестков и т. д.
– 7 лепестков и т. д.
А почему закономерность столь необычна, я только что проиллюстрировал геометрически.
Какой способ выбрать, решать вам, …но я бы не особо рекомендовал использовать обобщенные полярные координаты – у преподавателя могут появиться дополнительные вопросы на счет отрицательных значений полярного радиуса (а то и вообще всё будет забраковано по этой причине)
Короткая задача для самостоятельного решения:
Пример 5
Построить линии, заданные уравнением в полярных координатах
а) ![]()
б) ![]()
Сформулировать общее правило о количестве и длине лепестков полярной розы вида ![]() ,
, ![]() – натуральное)
– натуральное)
В моём образце решение проведено 1-м способом. Повторим порядок действий:
– Сначала находим область определения. При этом для лучшего понимания своих действий рекомендую соотносить аналитический способ «нарезки» с графической интерпретацией. По материалам урока Геометрические преобразования графиков выясните, как выглядят, и при необходимости начертите графики функций ![]() .
.
– Находим угловые координаты вершин лепестков – они расположены ровно посередине промежутков области определения.
– Выполняем чертёж. Пойдёт схематическая версия, однако желательно разметить найденные секторы и угловые направления вершин лепестков (в случае необходимости – с помощью транспортира). Вершины удобно засекать циркулем, предварительно установив раствор, равный длине лепестка.
Существуют более солидные и общие формулы окружности, полярной розы и желающие могут с ними ознакомиться в других источниках информации. Я лишь ограничился практически значимыми (с моей точки зрения) примерами.
Предлагаю перейти ко 2-й части занятия под названием Как построить линию в полярной системе координат?, где мы продолжим рассматривать типовые задачи, и усовершенствуем свои навыки.
Решения и ответы:
Пример 3. Решение: найдём область определения:
![]()
Вычислим полярные координаты точек, принадлежащих данной линии:
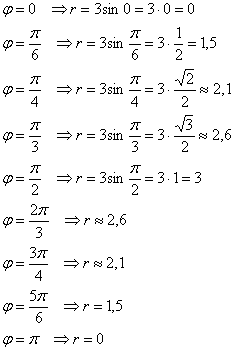
Выполним чертёж:
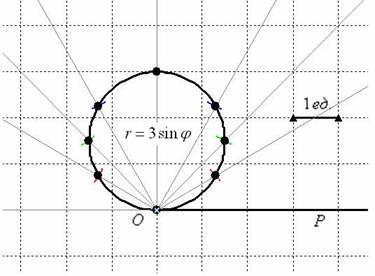
Найдём уравнение линии в декартовой системе координат:
![]()
Проведём замены ![]() :
:
![]()
Выделим полный квадрат:
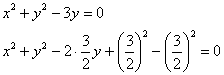
![]() – окружность с центром в точке
– окружность с центром в точке ![]() (координаты декартовы!) радиуса
(координаты декартовы!) радиуса ![]() .
.
Дополнительная информация: уравнение вида ![]() задаёт окружность диаметра
задаёт окружность диаметра ![]() с центром в точке
с центром в точке ![]() .
.
Пример 5. Решение:
а) Найдём область определения: косинус неотрицателен, когда его аргумент находится в пределах от ![]() до
до ![]() рад. включительно. В данном случае:
рад. включительно. В данном случае: ![]() . Или:
. Или:
![]() .
.
Таким образом:
– отрезок ![]() принадлежит области определения;
принадлежит области определения;
– интервал ![]() – не принадлежит;
– не принадлежит;
– отрезок ![]() – принадлежит;
– принадлежит;
– интервал ![]() – не принадлежит.
– не принадлежит.
Область определения: ![]() .
.
Роза имеет два лепестка, вершины которых находятся на полярной оси и её продолжении, длина лепестка равна ![]() :
:
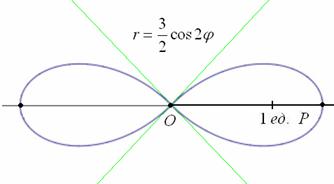
б) область определения: ![]() . Роза имеет три лепестка единичной длины с вершинами, имеющими следующие угловые координаты:
. Роза имеет три лепестка единичной длины с вершинами, имеющими следующие угловые координаты:
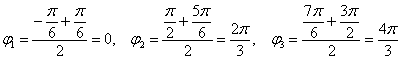
Выполним чертёж:
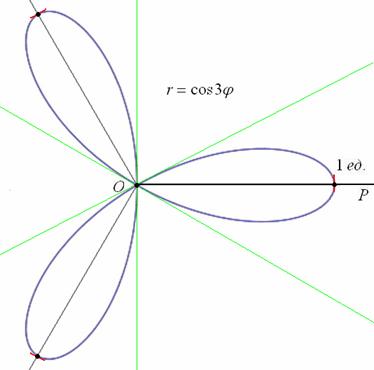
Уравнение вида ![]() ,
, ![]() – натуральное), задаёт полярную
– натуральное), задаёт полярную ![]() -лепестковую розу, длина лепестка которой равна
-лепестковую розу, длина лепестка которой равна ![]() . Если рассматривается обобщенная полярная система координат, то при чётном значения «ка» количество лепестков удваивается.
. Если рассматривается обобщенная полярная система координат, то при чётном значения «ка» количество лепестков удваивается.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright