


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как найти уравнение нормали к графику функции в заданной точке?
На данном уроке мы узнаем, как найти уравнение нормали к графику функции ![]() в точке
в точке ![]() и разберём многочисленные примеры, которые касаются этой задачи. Для качественного усвоения материала нужно понимать геометрический смысл производной и уметь их находить хотя бы на уровне следующих статей:
и разберём многочисленные примеры, которые касаются этой задачи. Для качественного усвоения материала нужно понимать геометрический смысл производной и уметь их находить хотя бы на уровне следующих статей:
Как найти производную?
Производная сложной функции
и
Простейшие задачи с производными.
Перечисленные уроки позволят «чайникам» быстро сориентироваться в теме и поднять свои навыки дифференцирования практически с полного нуля. По существу, сейчас последует развёрнутое продолжение параграфа об уравнении касательной 3-й статьи из вышеприведенного списка. Почему продолжение? Уравнение нормали тесно связано с уравнением касательной. Помимо прочего я рассмотрю задачи о том, как построить уравнения этих линий в ситуациях, когда функция задана неявно либо параметрически.
Но сначала освежим воспоминания: если функция ![]() дифференцируема в точке
дифференцируема в точке ![]() (т. е. если существует конечная производная
(т. е. если существует конечная производная ![]() ), то уравнение касательной к графику функции в точке
), то уравнение касательной к графику функции в точке ![]() можно найти по следующей формуле:
можно найти по следующей формуле:
![]()
Это самый распространенный случай, с которым мы уже столкнулись на уроке Простейшие задачи с производными. Однако дело этим не ограничивается: если в точке ![]() существует бесконечная производная:
существует бесконечная производная: ![]() , то касательная будет параллельна оси
, то касательная будет параллельна оси ![]() и её уравнение примет вид
и её уравнение примет вид ![]() . Дежурный пример: функция
. Дежурный пример: функция ![]() с производной
с производной ![]() , которая обращается в бесконечность вблизи критической точки
, которая обращается в бесконечность вблизи критической точки ![]() . Соответствующая касательная выразится уравнением:
. Соответствующая касательная выразится уравнением:
![]() (ось ординат).
(ось ординат).
Если же производной ![]() не существует (например, производной от
не существует (например, производной от ![]() в точке
в точке ![]() ), то, разумеется, не существует и общей касательной.
), то, разумеется, не существует и общей касательной.
Как различать последние два случая, я расскажу чуть позже, а пока что вернёмся в основное русло сегодняшнего урока.
Что такое нормаль? Нормалью к графику функции ![]() в точке
в точке ![]() называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке (понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.
называется прямая, проходящая через данную точку перпендикулярно касательной к графику функции в этой точке (понятно, что касательная должна существовать). Если совсем коротко, нормаль – это перпендикулярная к касательной прямая, проходящая через точку касания.
Как найти уравнение нормали? Из курса аналитической геометрии напрашивается очень простой алгоритм: находим уравнение касательной и представляем его в общем виде ![]() . Далее «снимаем» нормальный вектор
. Далее «снимаем» нормальный вектор ![]() и составляем уравнение нормали по точке
и составляем уравнение нормали по точке ![]() и направляющему вектору
и направляющему вектору ![]() .
.
Этот способ применять можно, но в математическом анализе принято пользоваться готовой формулой, основанной на взаимосвязи угловых коэффициентов перпендикулярных прямых. Если существует конечная и отличная от нуля производная ![]() , то уравнение нормали к графику функции
, то уравнение нормали к графику функции ![]() в точке
в точке ![]() выражается следующим уравнением:
выражается следующим уравнением:
![]()
Особые случаи, когда ![]() равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:
равна нулю либо бесконечности мы обязательно рассмотрим, но сначала «обычные» примеры:
Пример 1
Составить уравнения касательной и нормали к графику кривой ![]() в точке, абсцисса которой равна
в точке, абсцисса которой равна ![]() .
.
В практических заданиях часто требуется найти и касательную тоже. Впрочем, это очень только нА руку – лучше будет «набита рука» =)
Решение: первая часть задания хорошо знакома, уравнение касательной составим по формуле:
![]()
В данном случае:
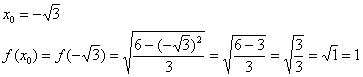
Найдём производную:
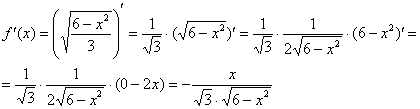
Здесь на первом шаге вынесли константу за знак производной, на втором – использовали правило дифференцирования сложной функции.
Теперь вычислим производную в точке ![]() :
:
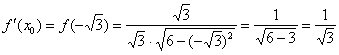
Получено конечное число и это радует. Подставим ![]() и
и ![]() в формулу
в формулу ![]() :
:
![]()
Перебросим ![]() наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:
наверх левой части, раскроем скобки и представим уравнение касательной в общем виде:
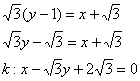
![]()
Вторая часть задания ничуть не сложнее. Уравнение нормали составим по формуле:
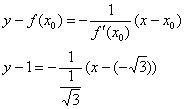
Избавляемся от трёхэтажности дроби и доводим уравнение до ума:
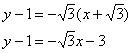
![]() – искомое уравнение.
– искомое уравнение.
Ответ: ![]()
Здесь можно выполнить частичную проверку. Во-первых, координаты точки ![]() должны удовлетворять каждому уравнению:
должны удовлетворять каждому уравнению:
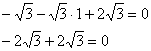
![]() – верное равенство.
– верное равенство.
![]()
![]() – верное равенство.
– верное равенство.
И, во-вторых, векторы нормали ![]() должны быть ортогональны. Это элементарно проверяется с помощью скалярного произведения:
должны быть ортогональны. Это элементарно проверяется с помощью скалярного произведения:
![]() , что и требовалось проверить.
, что и требовалось проверить.
Как вариант, вместо нормальных векторов можно использовать направляющие векторы прямых.
! Данная проверка оказывается бесполезной, если неверно найдена производная ![]() и / или производная в точке
и / или производная в точке ![]() . Это «слабое звено» задания – будьте предельно внимательны!
. Это «слабое звено» задания – будьте предельно внимательны!
Чертежа по условию не требовалось, но полноты картины ради:
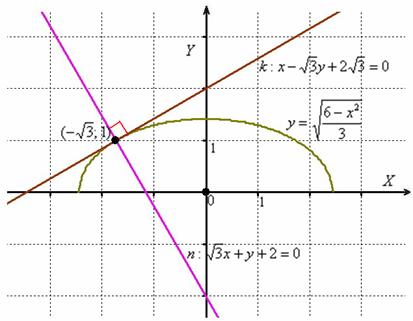
Забавно, но фактически получилась и полная проверка, поскольку чертёж выполнен достаточно точно =) Кстати, функция ![]() задаёт верхнюю дугу эллипса.
задаёт верхнюю дугу эллипса.
Следующая задача для самостоятельного решения:
Пример 2
Составить уравнения касательной и нормали к графику функции ![]() в точке
в точке ![]() .
.
Примерный образец чистового оформления задания в конце урока.
Теперь разберём два особых случая:
1) Если производная в точке ![]() равна нулю:
равна нулю: ![]() , то уравнение касательной упростится:
, то уравнение касательной упростится:
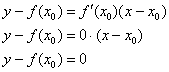
То есть касательная будет параллельна оси ![]() .
.
Соответственно, нормаль будет проходить через точку ![]() параллельно оси
параллельно оси ![]() , а значит её уравнение примет вид
, а значит её уравнение примет вид ![]() .
.
2) Если производная в точке ![]() существует, но бесконечна:
существует, но бесконечна: ![]() , то, как отмечалось в самом начале статьи, касательная станет вертикальной:
, то, как отмечалось в самом начале статьи, касательная станет вертикальной: ![]() . И поскольку нормаль проходит через точку
. И поскольку нормаль проходит через точку ![]() параллельно оси
параллельно оси ![]() , то её уравнение выразится «зеркальным» образом:
, то её уравнение выразится «зеркальным» образом: ![]()
Всё просто:
Пример 3
Составить уравнения касательной и нормали к параболе ![]() в точке
в точке ![]() . Сделать чертёж.
. Сделать чертёж.
Требование выполнить чертёж я не добавлял – так было сформулировано задание в оригинале. Хотя это редкость.
Решение: составим уравнение касательной ![]() .
.
В данном случае ![]()
Казалось бы, расчёты пустяковые, а в знаках запутаться более чем реально:
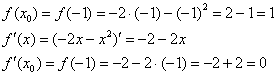
Таким образом:
![]()
Поскольку касательная параллельна оси ![]() (Случай № 1), то нормаль, проходящая через ту же точку
(Случай № 1), то нормаль, проходящая через ту же точку ![]() , будет параллельна оси ординат:
, будет параллельна оси ординат:
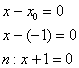
Чертёж – это, конечно же, дополнительные хлопоты, но зато добротная проверка аналитического решения:
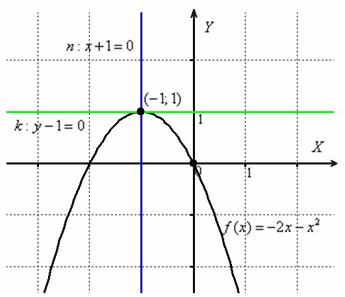
Ответ: ![]() ,
, ![]()
В школьном курсе математики распространено упрощенное определение касательной, которое формулируется примерно так: «Касательная к графику функции – это прямая, имеющая с данным графиком единственную общую точку». Как видите, в общем случае это утверждение некорректно. Согласно геометрическому смыслу производной, касательной является именно зелёная, а не синяя прямая.
Следующий пример посвящён тому же Случаю № 1, когда ![]() :
:
Пример 4
Написать уравнение касательной и нормали к кривой ![]() в точке
в точке ![]() .
.
Краткое решение и ответ в конце урока
Случай № 2, в котором ![]() на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались с определениями производной и касательной, а также имеют опыт нахождения производной по определению:
на практике встречается редко, поэтому начинающие могут особо не волноваться и с лёгким сердцем пропустить пятый пример. Информация, выделенная курсивом, предназначена для читателей с высоким уровнем подготовки, которые хорошо разобрались с определениями производной и касательной, а также имеют опыт нахождения производной по определению:
Пример 5
Найти уравнения касательной и нормали к графику функции ![]() в точке
в точке ![]()
Решение: в критической точке ![]() знаменатель производной
знаменатель производной ![]() обращается в ноль, и поэтому здесь нужно вычислить односторонние производные
обращается в ноль, и поэтому здесь нужно вычислить односторонние производные ![]() с помощью определения производной (см. конец статьи Производная по определению):
с помощью определения производной (см. конец статьи Производная по определению):
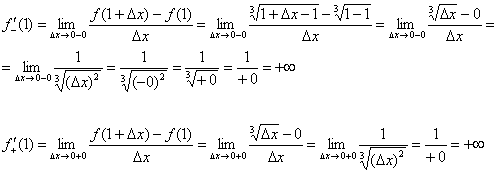
Обе производные бесконечны, следовательно, в точке ![]() существует общая вертикальная касательная:
существует общая вертикальная касательная:
![]()
Ну, и очевидно, что нормалью является ось абсцисс. Формально по формуле:
![]()
Для лучшего понимания задачи приведу чертёж:
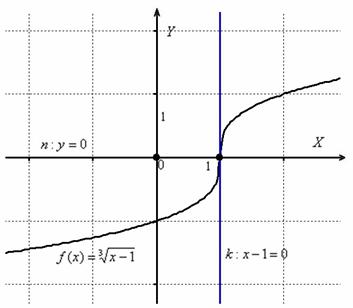
Ответ: ![]()
Я рад, что вы не ушли бороздить просторы Интернета, потому что всё самое интересное только начинается! Чтобы осилить материал следующего параграфа, нужно уметь находить производную неявно заданной функции:
Как найти уравнение касательной и уравнение нормали,
если функция задана неявно?
Формулы касательной и нормали остаются прежними, но меняется техника решения:
Пример 6
Найти уравнения касательной и нормали к кривой ![]() в точке
в точке ![]() .
.
Решение: судя по уравнению, это какая-то линия 3-го порядка, какая именно – нас сейчас совершенно не интересует.
В уравнении присутствует зловред ![]() , и поэтому перспектива выразить функцию в явном виде
, и поэтому перспектива выразить функцию в явном виде ![]() выглядит весьма туманной.
выглядит весьма туманной.
Но этого и не требуется! Есть куда более остроумное решение. Уравнение касательной составим по той же формуле ![]() .
.
Из условия известны значения ![]() , кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению:
, кстати, не помешает убедиться, что они действительно удовлетворяют предложенному уравнению:
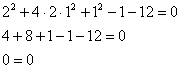
Получено верное равенство, значит, с точкой ![]() всё в порядке.
всё в порядке.
Осталось вычислить ![]() . Сначала по стандартной схеме найдём производную неявной функции:
. Сначала по стандартной схеме найдём производную неявной функции:
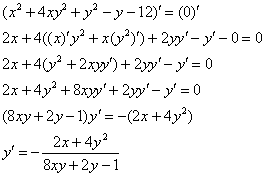
Перепишем результат с более подходящим для нашей задачи обозначением:
![]()
На 2-м шаге в найденное выражение производной подставим ![]() :
:
![]()
Вот так-то!
Осталось аккуратно разобраться с уравнением:
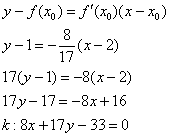
Составим уравнение нормали:
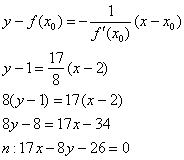
Ответ: ![]()
Готово! А поначалу представлялось всё непросто. Хотя производная здесь, конечно, – место уязвимое. Миниатюра для самостоятельного решения:
Пример 7
Найти уравнение нормали к линии ![]() в точке
в точке ![]()
Хватит уже вымучивать касательную =)
В данном случае легко выяснить, что это окружность ![]() центром в точке
центром в точке ![]() радиуса
радиуса ![]() и даже выразить нужную функцию
и даже выразить нужную функцию ![]() . Но зачем?! Ведь найти производную неявно заданной функции на порядок легче! Она тут чуть ли не самая примитивная.
. Но зачем?! Ведь найти производную неявно заданной функции на порядок легче! Она тут чуть ли не самая примитивная.
Краткое решение и ответ в конце урока.
Как найти уравнение касательной и уравнение нормали,
если функция задана параметрически?
Ещё проще. Но для этого нужно потренироваться в нахождении производных параметрически заданных функций. А так – почти халява:
Пример 8
Составить уравнения касательной и нормали к циклоиде ![]() , проведенные в точке, для которой
, проведенные в точке, для которой ![]() .
.
Чертёж циклоиды можно найти на странице S и V, если линия задана параметрически (в Примере 4 – так получилось, что та статья была создана раньше). И там даже изображена точка касания.
Решение: абсцисса и ордината точки касания рассчитываются непосредственно из параметрических уравнений кривой:
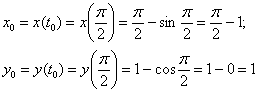
Найдём первую производную от параметрически заданной функции:
![]()
И вычислим её значение при ![]() :
:
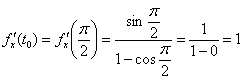
Уравнение касательной составим по обычной формуле с поправкой на несколько другие обозначения:
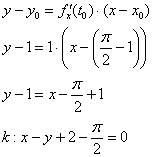
Уравнение нормали:
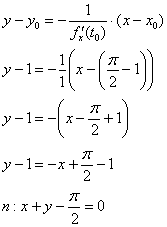
Ответ: ![]()
В заключение предлагаю познакомиться с ещё одной интересной линией:
Пример 9
Составить уравнение нормали к полукубической параболе 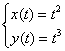 , проведенной в точке, для которой
, проведенной в точке, для которой ![]() .
.
Это пример для самостоятельного решения. Напоминаю, что графики параметрически заданных функций можно построить, например, с помощью моего расчётного геометрического макета.
Ну а наш урок подошёл к концу, и я надеюсь, что изложенный материал прошёл для вас не по касательной, а нормально =)
Спасибо за внимание и успехов!
Решения и ответы:
Пример 2. Решение: уравнение касательной составим по формуле:
![]()
В данном случае:
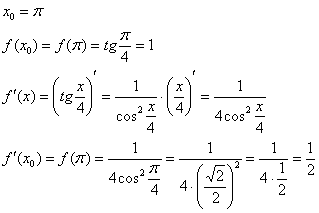
Таким образом:
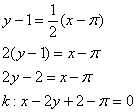
Уравнение нормали составим по формуле ![]() :
:
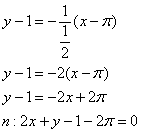
Ответ: ![]()
Пример 4. Решение: уравнение касательной составим по формуле:
![]()
В данной задаче:
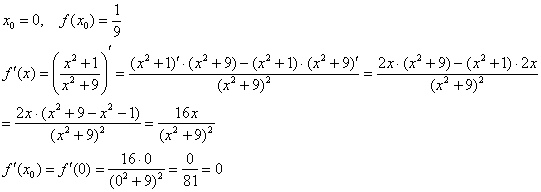
Таким образом:
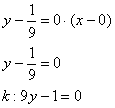
В точке ![]() касательная параллельна оси
касательная параллельна оси ![]() , поэтому соответствующее уравнение нормали:
, поэтому соответствующее уравнение нормали:
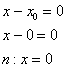
Ответ: ![]()
Пример 7. Решение: в данной задаче: ![]() .
.
Найдём производную:
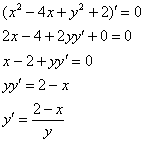
Или:
![]()
Подставим в выражение производной ![]() :
:
![]()
Искомое уравнение нормали:
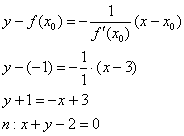
Ответ: ![]()
Пример 9. Решение: в данном случае:
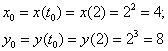
Найдём производную и вычислим её значение при ![]() :
:
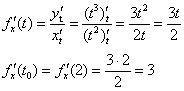
Уравнение нормали:
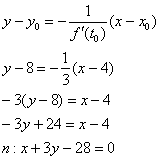
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright