


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Методы решения пределов. Неопределённости.
Порядок роста функции. Метод замены
На уроках Пределы. Примеры решений, Замечательные пределы мы рассмотрели азы темы, и данная статья продолжает наше погружение в мир пределов. Помимо закрепления материала, будет много новой информации о методах решения пределов, и, конечно же, примеры, примеры, примеры со всеми техническими тонкостями решений. Качественная проработка урока позволит выйти на уверенный средний уровень даже полному чайнику. Ну а для самоваров оглавление:
- Это грех
- Что является и что НЕ является неопределённостью?
- Порядок роста функции
- Сравнение бесконечно больших функций
- Если «икс» стремится к «минус» бесконечности
- Неопределённость «бесконечность минус бесконечность»
- Метод замены переменной в пределе
- Устранение неопределённости «единица в степени бесконечность»
Понеслось.
Что необходимо знать и уметь на данный момент?
– Вы должны ПОНИМАТЬ, что такое предел функции. Не выучить, не зазубрить, а именно понять хотя бы на общем, интуитивном уровне. Поэтому, если пределы сродни китайской грамоте, пожалуйста, начните с базового урока Пределы. Примеры решений, а также загляните в справку Графики и свойства элементарных функций, где я проиллюстрировал геометрический смысл понятия.
– Необходимо уметь использовать основные методы решения пределов и справляться с наиболее распространёнными заданиями. Очень хорошо, если кроме примеров моих первых двух уроков, вы порешали (или попытались порешать) что-нибудь дополнительно.
Есть? Едем дальше. Начнём с пары вопросов, которые вызвали недопонимание у некоторых посетителей сайта. За 2 года в отзывах и личной переписке мне удалось выяснить те моменты, которые недостаточно подробно рассмотрены в ранних статьях. И сейчас самое время акцентировать на них внимание.
Первый вопрос затрагивает саму сущность предела. В черновой версии урока я даже процитировал Винни-Пуха: «Куда идём мы с Пятачком, большой-большой секрет». Но потом убрал… нехорошо как-то… выходит все, кто этого не понял – медведи с опилками в голове.
«Чему равен предел ![]() ?» (пример условный)
?» (пример условный)
Действительно, чему?
Здесь не указано, куда стремится «икс», и такая запись не имеет смысла:
![]()
Предел функции не летает где-то по воздуху на воздушном шаре, он может существовать (или не существовать) только в определённой точке (в частности, в точке ![]() или
или ![]() ). Например:
). Например:
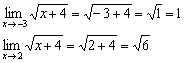
Заодно вспоминаем примитивный, но важный приём – чтобы вычислить предел, сначала нужно попытаться подставить значение «икс» в функцию. В случае с бесконечностью очевидно, что:
![]()
Иными словами, если ![]() , то функция
, то функция ![]() неограниченно возрастает.
неограниченно возрастает.
А вот следующего предела не существует:
![]()
Значение ![]() не входит в область определения функции (под корнем получается «минус»).
не входит в область определения функции (под корнем получается «минус»).
рАвно не существует и такого предела:
![]()
Тут «икс» стремится к «минус» бесконечности, и под корнем нарисуется бесконечно большое отрицательное значение.
Итак, в природе не существует «просто предела». Предел может существовать (или не существовать) лишь в определённой точке, в частности, в точке «плюс» бесконечность или «минус» бесконечность.
В процессе оформления практических примеров постарайтесь придерживаться следующей рекомендации: не допускайте неполной записи вроде ![]() , это одна из самых скверных оплошностей. Презумпция виновности студента утверждает, что он либо совсем не в теме, либо откуда-то впопыхах списал пример.
, это одна из самых скверных оплошностей. Презумпция виновности студента утверждает, что он либо совсем не в теме, либо откуда-то впопыхах списал пример.
Второй вопрос касается путаницы с неопределённостями, которые возникают в ходе решения более сложных пределов. Систематизируем информацию:
Что в пределах функций ЯВЛЯЕТСЯ неопределённостью
и НЕ ЯВЛЯЕТСЯ неопределённостью
Прежде всего, перед решением любого предела, обязательно выполняем подстановку «икса» в функцию – неопределённости может и не быть! Однако сладостей много вредно, и на первых двух уроках мы сталкивались со следующими неопределённостями:
![]()
Кроме указанных видов, существует довольно распространённая неопределённость ![]() («бесконечность минус бесконечность»), которую мы подробно разберём в этой статье, и совсем редко встречаются неопределённости
(«бесконечность минус бесконечность»), которую мы подробно разберём в этой статье, и совсем редко встречаются неопределённости ![]() .
.
Для того чтобы устранить неопределённость, как вы знаете, необходимо использовать некоторые правила и методы решения пределов.
Теперь о том, ЧТО НЕ ЯВЛЯЕТСЯ неопределённостью.
Неопределённостью не является:
– Любая определённость =)
– Бесконечно малое значение, делённое на ненулевую константу: ![]() . Сюда же можно отнести бесконечно малую величину, делённую на бесконечно большую величну:
. Сюда же можно отнести бесконечно малую величину, делённую на бесконечно большую величну: ![]()
– Константа, делённая на бесконечно малую величину, например: ![]() .
.
– Начинающие изучать математический анализ, часто пытаются устранить мифическую неопределённость ![]() . Но все попытки тщетны, поскольку это определённость:
. Но все попытки тщетны, поскольку это определённость:
представим «бесконечность делить на ноль» в виде произведения: ![]() , и, согласно предыдущему пункту:
, и, согласно предыдущему пункту: ![]() . Приведу живой пример:
. Приведу живой пример:
![]()
Примечание: на практике в нашей теме значок ![]() , как я уже отмечал, часто записывают без «плюса»:
, как я уже отмечал, часто записывают без «плюса»: ![]() , но, строго говоря, это две разные вещи
, но, строго говоря, это две разные вещи
– Неотрицательное число в бесконечно большой степени не является неопределённостью. Например: ![]() . В частности:
. В частности: ![]() . Заметим, что строгая единица в бесконечно большой степени – есть единица, в то время, как в символическом обозначении неопределённости
. Заметим, что строгая единица в бесконечно большой степени – есть единица, в то время, как в символическом обозначении неопределённости ![]() подразумевается бесконечно близкое к единице значение, и там ещё бабушка надвое сказала, что получится. Отрицательное же число в бесконечно большой степени – не определено (предела не существует).
подразумевается бесконечно близкое к единице значение, и там ещё бабушка надвое сказала, что получится. Отрицательное же число в бесконечно большой степени – не определено (предела не существует).
– Разность двух функций, каждая из которых стремится к нулю, например: ![]() . Таким образом, неопределённости «ноль минус ноль» тоже не существует – это определённость.
. Таким образом, неопределённости «ноль минус ноль» тоже не существует – это определённость.
Многие из перечисленных неопределённостей и определённостей уже встречались и ещё неоднократно встретятся на практике.
До нового 2013 года остаются считанные дни, и в качестве подарка я принёс увесистый ящик с петардами:
Порядок роста функции
В данном параграфе будут разобраны пределы с многочленами, многочленами под корнем, когда ![]() или
или ![]() . Материал вам уже частично знаком, и настала пора разобраться в нём как следует. Давайте научимся находить решение в считанные секунды!
. Материал вам уже частично знаком, и настала пора разобраться в нём как следует. Давайте научимся находить решение в считанные секунды!
Вычислим следующий предел:
![]()
На базовом уроке Пределы. Примеры решений я рекомендовал рассуждать не совсем корректным способом: сначала «икс» равно 10, потом, 100, затем 1000, миллион и т. д. до бесконечности. В чём изъян такого подхода? Построим данную последовательность:
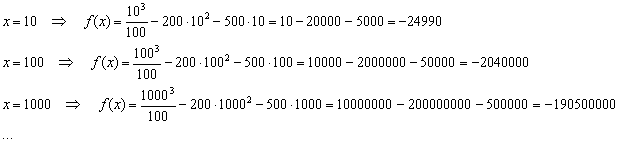
Исходя из полученных результатов, складывается стойкое впечатление, что предел стремится к «минус» бесконечности, но на поверку впечатление кардинально ошибочно:
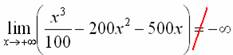
В этой связи необходимо знать теорию матана, а именно, некоторые выкладки о порядке роста функции. Простыми словами – это то, насколько быстро растёт та или иная функция.
Применительно к нашему примеру можно сказать, что слагаемое ![]() обладает более высоким порядком роста, чем сумма
обладает более высоким порядком роста, чем сумма ![]() . Иными словами, при достаточно больших значениях «икс» слагаемое
. Иными словами, при достаточно больших значениях «икс» слагаемое ![]() «перетянет» на «плюс» бесконечность всё остальное:
«перетянет» на «плюс» бесконечность всё остальное:
![]()
При небольших значениях «икс» – да, сладкая парочка ![]() перетягивает канат в сторону «минус» бесконечности, что и привело нас к неверному первоначальному выводу. Но уже при
перетягивает канат в сторону «минус» бесконечности, что и привело нас к неверному первоначальному выводу. Но уже при ![]() получается гигантское положительное число
получается гигантское положительное число ![]() .
.
Если сильно уменьшить первое слагаемое, то от этого ничего не изменится: ![]() , будет лишь отсрочен тот момент, когда бравая дробь
, будет лишь отсрочен тот момент, когда бравая дробь ![]() «вытянет» весь предел на «плюс» бесконечность. Не поможет и «усиление противовеса»:
«вытянет» весь предел на «плюс» бесконечность. Не поможет и «усиление противовеса»:
![]() .
.
Нулей можете приписать, сколько хотите (без шуток). Удивительная наука математический анализ – способна низвести любого монстра до мелочи пузатой.
Таким образом, кубическая функция имеет более высокий порядок роста, чем:
– квадратичная функция;
– линейная функция;
– сумма квадратичной и линейной функции.
На простейшем примере поясню геометрический смысл вышесказанного. Представьте графики линейной ![]() , квадратичной
, квадратичной ![]() и кубической
и кубической ![]() функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола
функций (см. методичку Графики и свойства функций). Легко заметить, что при увеличении значений «икс», кубическая парабола ![]() взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.
взмывает вверх гораздо быстрее и круче, чем парабола и, тем более, прямая.
Аналогичное правило можно сформулировать для любой положительной степени:
степеннАя функция данной степени с произвольным ненулевым коэффициентом (множителем) растёт быстрее, чем любая степенная функция более низкой положительной степени. И быстрее, чем сумма любого количества таких функций, вне зависимости от их числовых коэффициентов.
Найдём предел ![]()
Значение этого предела зависит только от слагаемого ![]() . Всё остальное МЫСЛЕННО отбрасываем:
. Всё остальное МЫСЛЕННО отбрасываем: ![]() , и теперь ясно как день, что предел равен «минус» бесконечности:
, и теперь ясно как день, что предел равен «минус» бесконечности:
![]()
То есть слагаемое ![]() более высокого порядка роста, чем всё остальное.
более высокого порядка роста, чем всё остальное.
У «хвоста» ![]() могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ, при этом у «мажора»
могут быть сколь угодно большие константы, другие знаки, но результат от этого НЕ ИЗМЕНИТСЯ, при этом у «мажора» ![]() вместо «–2» может быть любой отрицательный коэффициент, даже очень малый. Заметим заодно, что если он положителен, то предел будет равен уже «плюс» бесконечности.
вместо «–2» может быть любой отрицательный коэффициент, даже очень малый. Заметим заодно, что если он положителен, то предел будет равен уже «плюс» бесконечности.
Сравнение бесконечно больших функций
На первом уроке мы вычислили три предела с неопределённостью ![]() :
:
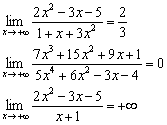
В перечисленных примерах используется стандартный приём деления числителя и знаменателя на «икс» в старшей степени и всё расписывается подробно. Но правильный ответ легко выяснить ещё до решения!
В первом примере ![]() в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:
в числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые:
![]() – получено конечное число, отличное от нуля.
– получено конечное число, отличное от нуля.
В таких случаях говорят, что функции числителя и знаменателя обладают одинаковым порядком роста. Или короче – числитель и знаменатель одного порядка роста. Действительно, в данном пределе и вверху, и внизу находятся квадратичные функции. Мир, равенство, братство.
Во втором примере ![]() аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:
аналогично – в числителе и знаменателе МЫСЛЕННО уберём всех малышей:
![]()
Здесь знаменатель более высокого порядка, чем числитель. Функция-многочлен 4-й степени растёт быстрее кубической функции и «перетягивает» предел на ноль.
И, наконец, в пределе ![]() карлики тоже идут лесом:
карлики тоже идут лесом:
![]()
А в этом примере всё наоборот – числитель более высокого порядка, чем знаменатель. Квадратичная функция растёт быстрее линейной и «перетягивает» предел на «плюс» бесконечность.
Сделаем краткую теоретическую выжимку. Рассмотрим две произвольные функции ![]() , которые стремятся к «плюс» или «минус» бесконечности при
, которые стремятся к «плюс» или «минус» бесконечности при ![]() .
.
1) Если ![]() , где
, где ![]() – ненулевая константа, то функции имеют одинаковый порядок роста. Если
– ненулевая константа, то функции имеют одинаковый порядок роста. Если ![]() , то функции называют эквивалентными на бесконечности.
, то функции называют эквивалентными на бесконечности.
2) Если ![]() , то функция
, то функция ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() .
.
3) Если ![]() , то функция
, то функция ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() .
.
! Примечание: при ![]() суть выкладок не меняется. Кроме того, функции могут быть бесконечно большими и аналогично сравнимыми и в конечной точке.
суть выкладок не меняется. Кроме того, функции могут быть бесконечно большими и аналогично сравнимыми и в конечной точке.
Подчеркиваю ещё раз, что данные факты относятся к произвольным функциям, определённым на бесконечности, а не только к многочленам. Но у нас ещё непаханое поле полиномов, поэтому, продолжаем работать с ними…, да вы не грустите, для разнообразия я корней добавлю =), опытные алгебраисты прослезились:
Пример 1
Найти предел ![]()
В наличии неопределённость ![]() и приём решения уже знаком – нужно разделить числитель и знаменатель на «икс» в старшей степени.
и приём решения уже знаком – нужно разделить числитель и знаменатель на «икс» в старшей степени.
Старшая степень числителя равна двум. Знаменатель…. Как определить старшую степень, если многочлен под корнем? МЫСЛЕННО отбрасываем все слагаемые, кроме самого старшего: ![]() . Константу тоже отбрасываем и выясняем старшую степень знаменателя:
. Константу тоже отбрасываем и выясняем старшую степень знаменателя: ![]() . Она тоже равна двум. Таким образом, числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу, отличному от нуля.
. Она тоже равна двум. Таким образом, числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу, отличному от нуля.
Почему бы сразу не узнать ответ? В числителе и знаменателе МЫСЛЕННО отбрасываем все младшие слагаемые: ![]() . Таким образом, наши функции не только одного порядка роста, но ещё и эквивалентны на бесконечности.
. Таким образом, наши функции не только одного порядка роста, но ещё и эквивалентны на бесконечности.
Оформляем решение:
![]()
Разделим числитель и знаменатель на ![]()
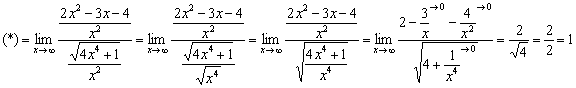
В действительности пару шагов можно пропустить, просто я подробно расписал, как в знаменателе под корень вносится ![]() .
.
Пример 2
Найти предел ![]()
Это пример для самостоятельного решения. Постарайтесь провести рассуждения по образцу первого примера. Также заметьте, что здесь неопределённость ![]() , что крайне желательно отразить в решении. Примерный образец чистового оформления примера в конце урока.
, что крайне желательно отразить в решении. Примерный образец чистового оформления примера в конце урока.
Во избежание недочёта, всегда анализируйте, какая неопределённость получается в пределах рассматриваемого вида. Помимо неопределённости ![]() может встретиться неопределённость
может встретиться неопределённость ![]() либо
либо ![]() . Во всех четырёх случаях числитель и знаменатель нужно разделить на «икс» в старшей степени.
. Во всех четырёх случаях числитель и знаменатель нужно разделить на «икс» в старшей степени.
Пример 3
Найти предел 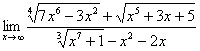
Слишком трудный предел? Лёгкий испуг от хлопушки. Главное, грамотно управиться с радикалами.
Проведём предварительный анализ:
Сначала выясним старшую степень числителя. Там сумма двух корней. Под корнем ![]() отбросим младшее слагаемое:
отбросим младшее слагаемое: ![]() и уберём константу:
и уберём константу: ![]() . Под корнем
. Под корнем ![]() отбросим все младшие слагаемые:
отбросим все младшие слагаемые: ![]() .
.
![]() , значит, старшая степень числителя:
, значит, старшая степень числителя: ![]() .
.
Разбираемся с нижним этажом. Под корнем ![]() отбрасываем константу:
отбрасываем константу: ![]() . У многочлена
. У многочлена ![]() старшая степень равна двум.
старшая степень равна двум.
![]() , значит, старшая степень знаменателя:
, значит, старшая степень знаменателя: ![]() .
.
Кстати, заметьте, что корень ![]() более высокого порядка роста, чем
более высокого порядка роста, чем ![]() , поэтому весь знаменатель будет стремиться к «плюс» бесконечности.
, поэтому весь знаменатель будет стремиться к «плюс» бесконечности.
Сравниваем старшие степени: ![]() , следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности.
, следовательно, числитель более высокого порядка роста, чем знаменатель, и сразу можно сказать, что предел будет равен бесконечности.
Оформляем решение, я распишу его максимально подробно:
![]()
Разделим числитель и знаменатель на «икс» в старшей степени: ![]() :
:
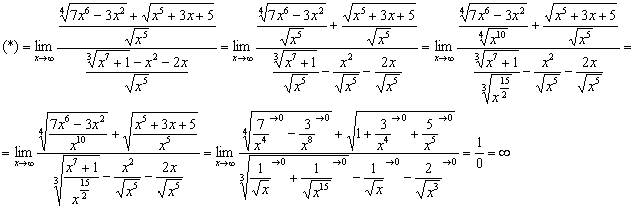
Действия в числителе прозрачны, закомментирую знаменатель. У дроби ![]() «разнокалиберные» корни, и квадратный корень
«разнокалиберные» корни, и квадратный корень ![]() нужно «подогнать» под кубический корень
нужно «подогнать» под кубический корень ![]() . Составим и решим уравнение:
. Составим и решим уравнение: ![]() . Таким образом:
. Таким образом: 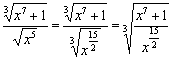 .
.
Ну и на всякий случай напоминаю формулу ![]() , по которой выполняется деление:
, по которой выполняется деление:
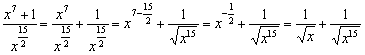
Другие члены знаменателя:
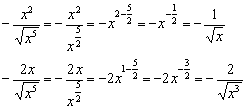
Правила действий с корнями можно найти на странице Математические формулы и таблицы в методичке Горячие формулы школьного курса математики. Также на действиях с радикалами я подробно останавливался при нахождении производных.
Пример 4
Найти предел ![]()
Это более простой пример для самостоятельного решения. В предложенном примере снова неопределённость ![]() (
(![]() более высокого порядка роста, чем корень
более высокого порядка роста, чем корень ![]() ).
).
Если «икс» стремится к «минус» бесконечности
Призрак «минус» бесконечности уже давно витал в этой статье. Рассмотрим пределы с многочленами, в которых ![]() . Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
. Принципы и методы решения будут точно такими же, что и в первой части урока, за исключением ряда нюансов.
Рассмотрим 4 фишки, которые потребуются для решения практических заданий:
1) Вычислим предел ![]()
Значение предела зависит только от слагаемого ![]() , поскольку оно обладает самым высоким порядком роста. Если
, поскольку оно обладает самым высоким порядком роста. Если ![]() , то бесконечно большое по модулю отрицательное значение в ЧЁТНОЙ степени, в данном случае – в четвёртой, равно «плюс» бесконечности:
, то бесконечно большое по модулю отрицательное значение в ЧЁТНОЙ степени, в данном случае – в четвёртой, равно «плюс» бесконечности: ![]() . Константа («двойка») положительна, поэтому:
. Константа («двойка») положительна, поэтому:
![]()
2) Вычислим предел ![]()
Здесь старшая степень опять чётная, поэтому: ![]() . Но перед
. Но перед ![]() расположился «минус» (отрицательная константа –1), следовательно:
расположился «минус» (отрицательная константа –1), следовательно:
![]()
3) Вычислим предел ![]()
Значение предела зависит только от ![]() . Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное значение в НЕЧЁТНОЙ степени равно «минус» бесконечности, в данном случае:
. Как вы помните из школы, «минус» «выскакивает» из-под нечётной степени, поэтому бесконечно большое по модулю отрицательное значение в НЕЧЁТНОЙ степени равно «минус» бесконечности, в данном случае: ![]() .
.
Константа («четвёрка») положительна, значит:
![]()
4) Вычислим предел ![]()
Первый парень на деревне ![]() снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит:
снова обладает нечётной степенью, кроме того, за пазухой отрицательная константа, а значит: ![]() Таким образом:
Таким образом:
![]() .
.
Пример 5
Найти предел ![]()
Используя вышеизложенные пункты, приходим к выводу, что здесь неопределённость ![]() . Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
. Числитель и знаменатель одного порядка роста, значит, в пределе получится конечное число. Узнаем ответ, отбросив всех мальков:
![]()
Решение тривиально:
![]()
Разделим числитель и знаменатель на ![]()
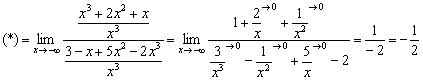
Пример 6
Найти предел ![]()
Это пример для самостоятельного решения. Полное решение и ответ в конце урока.
А сейчас, пожалуй, самый тонкий из случаев:
Пример 7
Найти предел ![]()
Рассматривая старшие слагаемые, приходим к выводу, что здесь неопределённость ![]() . Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
. Числитель более высокого порядка роста, чем знаменатель, поэтому сразу можно сказать, что предел равен бесконечности. Но какой бесконечности, «плюс» или «минус»? Приём тот же – в числителе и знаменателе избавимся от мелочи:
![]()
Решаем:
![]()
Разделим числитель и знаменатель на ![]()
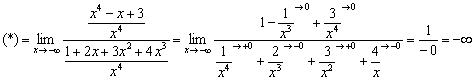
Почему ![]() ?
?
Проанализируем бесконечно малые слагаемые знаменателя:
Если ![]() , то слагаемые с чётными степенями
, то слагаемые с чётными степенями ![]() будут стремиться к бесконечно малым положительным числам (обозначаются через
будут стремиться к бесконечно малым положительным числам (обозначаются через ![]() ), а слагаемые с нечётными степенями
), а слагаемые с нечётными степенями ![]() будут стремиться к бесконечно малым отрицательным числам (обозначаются через
будут стремиться к бесконечно малым отрицательным числам (обозначаются через ![]() ).
).
Теперь зададимся вопросом, какое из этих четырёх слагаемых ![]() будет стремиться к нулю (неважно с каким знаком) медленнее всего? Применим пижонский анализ: сначала «икс» равно -10, потом -100, затем -1000 и т. д. Медленнее всего к нулю будет приближаться слагаемое
будет стремиться к нулю (неважно с каким знаком) медленнее всего? Применим пижонский анализ: сначала «икс» равно -10, потом -100, затем -1000 и т. д. Медленнее всего к нулю будет приближаться слагаемое ![]() . Образно говоря, это самый «жирный» ноль, который «поглощает» все остальные нули. По этой причине на завершающем этапе и появилась запись
. Образно говоря, это самый «жирный» ноль, который «поглощает» все остальные нули. По этой причине на завершающем этапе и появилась запись ![]() .
.
Следует отметить, что знаки бесконечно малых слагаемых числителя нас не интересуют, поскольку там нарисовалась осязаемая добротная единичка. Поэтому в числителе я поставил «просто нули». К слову, знаки при нулях не имеют значения и во всех примерах, где в пределе получается конечное число (Примеры № 5, 6).
Без измен, на то он и математический анализ, чтобы анализировать =)
Впрочем, о бесконечно малых функциях позже, а то вы нажмёте маленький крестик справа вверху =)
Пример 8
Найти предел ![]()
Это пример для самостоятельного решения.
Рекомендую хорошо осмыслить информацию первой части урока, и по возможности сделать перерыв.
Неопределённость «бесконечность минус бесконечность»
Популярная неопределённость ![]() устраняется тремя распространёнными способами:
устраняется тремя распространёнными способами:
– приведением выражения под знаком предела к общему знаменателю;
– умножением / делением на сопряжённое выражение;
– преобразованием логарифмов.
Рассмотрим первый случай, о котором я ещё не рассказывал:
Пример 9
Вычислить предел
![]()
В данном пределе имеет место неопределённость ![]() , и общий алгоритм решения незамысловат: нужно привести выражение к общему знаменателю, а затем попытаться что-нибудь сократить:
, и общий алгоритм решения незамысловат: нужно привести выражение к общему знаменателю, а затем попытаться что-нибудь сократить:
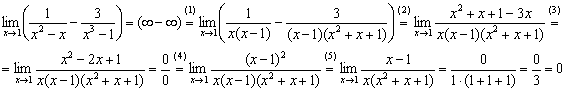
(1) Раскладываем знаменатели на множители: в первом знаменателе выносим «икс» за скобки, во втором знаменателе используем формулу разности кубов ![]() . Данный шаг можно было пропустить, но этим пришлось бы заниматься потом, и, на мой взгляд, разложение на множители удобнее провести сразу же.
. Данный шаг можно было пропустить, но этим пришлось бы заниматься потом, и, на мой взгляд, разложение на множители удобнее провести сразу же.
(2) Приводим выражение к общему знаменателю.
(3) Приводим подобные слагаемые в числителе. Неопределённость ![]() трансформировалась в неопределённость
трансформировалась в неопределённость ![]() , которая стандартно раскрывается разложением числителя и знаменателя на множители.
, которая стандартно раскрывается разложением числителя и знаменателя на множители.
(4) Знаменатель уже разложен на множители. Раскладываем на множители числитель, в данном случае использована формула ![]() .
.
(5) Сокращаем числитель и знаменатель на ![]() , устраняя неопределённость.
, устраняя неопределённость.
Как видите, новизны-то особой и нет.
Аналогичное задание для самостоятельного решения:
Пример 10
Вычислить предел
![]()
Решение и ответ в конце урока
Второй вид пределов с неопределённостью ![]() представляет собой разность, в которой присутствуют два или один корень:
представляет собой разность, в которой присутствуют два или один корень:
Пример 11
Вычислить предел
![]()
Каноничный образец. Метод решения подробно разобран на уроке Пределы. Примеры решений. Здесь следует умножить и разделить на сопряженное выражение, чтобы потом воспользоваться формулой ![]()
![]()
Умножим и разделим на сопряженное выражение:
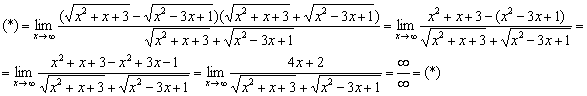
Неопределённость ![]() превратилась в неопределённость
превратилась в неопределённость ![]() . Узнаёте? Такие семечки мы грызли в первом разделе данного урока.
. Узнаёте? Такие семечки мы грызли в первом разделе данного урока.
Числитель и знаменатель одного порядка роста, а значит, предел равен конечному числу. Разделим числитель и знаменатель на ![]() :
:
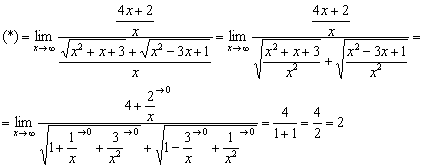
Не редкость, когда в разности всего один корень, но это не меняет алгоритма решения:
Пример 12
Вычислить предел
![]()
Пример 13
Вычислить предел
![]()
Это пара коротких примеров для самостоятельного решения.
Следует отметить, что пределы рассмотренного типа не обязаны равняться конечному числу, вполне может получиться и бесконечность, причём, как «плюс», так и «минус». Кстати, в примере № 13 можно посмотреть на порядок роста членов, чтобы сразу выяснить ответ ;-)
Иногда на практике встречаются пределы-«обманки», в которых неопределённости «бесконечность минус бесконечность» нет вообще, вот простой пример:
![]()
Таким образом, будьте предельно внимательны: перед решением предела необходимо убедиться, что неопределённость ![]() действительно есть!
действительно есть!
В заключительной части статьи вернёмся к незаслуженно забытым замечательным пределам, где рассмотрим, в том числе, третий тип пределов с неопределённостью ![]() .
.
Метод замены переменной в пределе
Весьма ходовой приём решения. Метод замены переменной применяют чаще всего для того, чтобы свести решение к первому замечательному пределу, намного реже – к другому замечательному пределу. Рассмотрим пару типовых образцов:
Пример 14
Найти предел
![]()
Решаем:
![]()
В пределе находится арктангенс, от которого хорошо бы избавиться. Логично и очень удобно превратить «арк» в одну единственную букву. Проведём замену переменной: ![]() .
.
Теперь в пределе нужно выразить всё остальное через «тэ».
Во-первых, выясним, куда будет стремиться новая переменная «тэ»:
Если ![]() , то
, то ![]() , иными словами, новоиспеченная переменная тоже будет стремиться к нулю:
, иными словами, новоиспеченная переменная тоже будет стремиться к нулю: ![]()
Осталось в знаменателе выразить «икс» через «тэ». Для этого на обе части равенства ![]() «навешиваем» тангенсы:
«навешиваем» тангенсы:
![]()
В правой части две взаимно обратные функции уничтожаются:
![]() , откуда:
, откуда: ![]()
Взмахи волшебной палочки закончены, остальное просто:
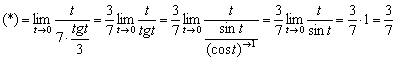
Используемые формулы и приёмы решения завершающего этапа очень подробно разобраны в первой части урока Замечательные пределы.
Пример 15
Найти предел
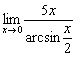
Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.
Ещё пара занятных примеров на тему замены переменной:
Пример 16
Найти предел
![]()
При подстановке единицы в предел получается неопределённость ![]() . Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле
. Замена переменной уже напрашивается, но сначала преобразуем тангенс по формуле ![]() . Действительно, зачем нам тангенс?
. Действительно, зачем нам тангенс?
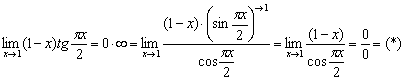
Заметьте, что ![]() , поэтому
, поэтому ![]() . Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице. Таким образом, мы сразу избавляемся от множителя
. Если не совсем понятно, посмотрите значения синуса в тригонометрической таблице. Таким образом, мы сразу избавляемся от множителя ![]() , кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
, кроме того, получаем более привычную неопределённость 0:0. Хорошо бы ещё и предел у нас стремился к нулю.
Проведем замену: ![]()
Если ![]() , то
, то ![]()
Под косинусом у нас находится «икс», который тоже нужно выразить через «тэ».
Из замены ![]() выражаем:
выражаем: ![]() .
.
Завершаем решение:
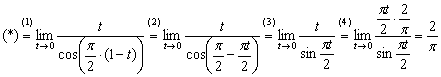
(1) Проводим подстановку
(2) Раскрываем скобки под косинусом.
(3) Используем формулу приведения ![]() , формулы приведения также можно найти в тригонометрических таблицах.
, формулы приведения также можно найти в тригонометрических таблицах.
(4) Чтобы организовать первый замечательный предел («перевёртыш»), искусственно домножаем числитель на ![]() и обратное число
и обратное число ![]() .
.
Задание для самостоятельного решения:
Пример 17
Найти предел
![]()
Полное решение и ответ в конце урока.
Это были несложные задачи в своём классе, на практике всё бывает хуже, и, помимо формул приведения, приходится использовать самые разные тригонометрические формулы, а также прочие ухищрения. В статье Сложные пределы я разобрал пару настоящих примеров =)
В канун праздника окончательно проясним ситуацию ещё с одной распространённой неопределённостью:
Устранение неопределённости «единица в степени бесконечность»
Данную неопределённость «обслуживает» второй замечательный предел, и во второй части того урока мы очень подробно рассмотрели стандартные примеры решений, которые в большинстве случаев встречаются на практике. Сейчас картина с экспонентами будет завершена, кроме того, заключительные задания урока будут посвящены пределам-«обманкам», в которых КАЖЕТСЯ, что необходимо применить 2-й замечательный предел, хотя это вовсе не так.
Недостаток двух рабочих формул 2-го замечательного предела состоит в том, что аргумент должен стремиться к бесконечности либо к нулю. Но что делать, если аргумент стремится к другому числу?
На помощь приходит универсальная формула (которая на самом деле является следствием второго замечательного предела):
Неопределённость ![]() можно устранить по формуле:
можно устранить по формуле:
![]()
Где-то вроде уже пояснял, что обозначают квадратные скобки. Ничего особенного, скобки как скобки. Обычно их используют, чтобы чётче выделить математическую запись.
Выделим существенные моменты формулы:
1) Речь идёт о неопределённости ![]() .
.
2) Аргумент «икс» может стремиться к произвольному действительному значению (а не только к нулю или бесконечности).
С помощью данной формулы можно решить все примеры урока Замечательные пределы, которые относятся ко 2-му замечательному пределу. Например, вычислим предел ![]() :
:
В данном случае ![]() , и по формуле
, и по формуле ![]() :
:
![]()
Правда, делать так не советую, в традициях всё-таки применять «обычное» оформление решения, если его можно применить. Однако с помощью формулы очень удобно выполнять проверку «классических» примеров на 2-й замечательный предел.
Всё это хорошо, правильно, но сейчас в кадре более любопытные кадры:
Пример 18
Вычислить предел
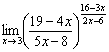
На первом шаге, не устану повторять, подставляем значение «икс» в выражение под знаком предела. А вдруг никакой неопределённости вообще нет? Так бывает! Но не в этот раз. Подставляя «тройку», приходим к выводу, что здесь неопределённость ![]()
Используем формулу ![]()
Чтобы не таскать за собой букву «е» и не мельчить, показатель ![]() удобнее вычислить отдельно:
удобнее вычислить отдельно:
В данном случае: ![]()
Таким образом:
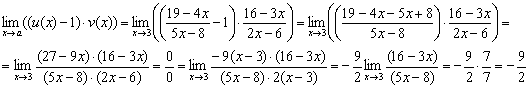
С точки зрения техники вычислений всё рутинно: сначала приводим первое слагаемое к общему знаменателю, затем выносим константы и проводим сокращения, избавляясь от неопределённости 0:0.
В результате:
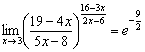
Готово.
Обещанный подарок с разностью логарифмов и неопределённостью ![]() :
:
Пример 19
Вычислить предел
![]()
Сначала полное решение, потом комменты:
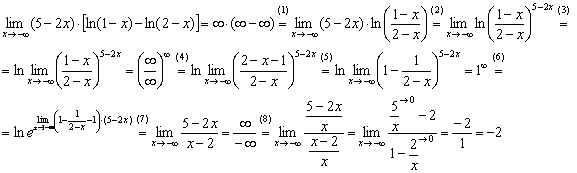
(1)-(2) На первых двух шагах используем формулы ![]() . У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
. У сложных производных мы «разваливаем» логарифмы, а здесь, наоборот – их нужно «собрать».
(3) Значок предела перемещаем под логарифм. Это можно сделать, поскольку данный логарифм непрерывен на «минус» бесконечности. Кроме того, предел же относится к «начинке» логарифма.
(4)-(5) Стандартным приёмом, рассмотренным на базовом уроке про замечательные пределы, преобразуем неопределённость ![]() к виду
к виду ![]() .
.
(6) Используем формулу ![]() .
.
(7) Экспоненциальная и логарифмическая функция – взаимно обратные функции, поэтому и «е» и логарифм можно убрать. Действительно, согласно свойству логарифма: ![]() . Минус перед дробью вносим в знаменатель:
. Минус перед дробью вносим в знаменатель: ![]()
(8) Без комментариев =)
Рассмотренный тип предела не такой редкий, примеров 30-40 у себя нашёл.
Пример 20
Вычислить предел
![]()
Это пример для самостоятельного решения. Помимо использования формулы, можно представить предел в виде ![]() и заменой
и заменой ![]() свести решение к случаю
свести решение к случаю ![]() .
.
В заключение рассмотрим пределы-«фальшивки».
Вернёмся к неопределённости ![]() . Данную неопределённость далеко не всегда можно свести к неопределённости
. Данную неопределённость далеко не всегда можно свести к неопределённости ![]() и воспользоваться 2-м замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции. На пример:
и воспользоваться 2-м замечательным пределом либо формулой-следствием. Преобразование осуществимо в том случае, если числитель и знаменатель основания степени – эквивалентные бесконечно большие функции. На пример: ![]() .
.
Отвлечёмся от показателя и вычислим предел основания:
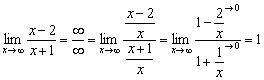
В пределе получена единица, значит, числитель и знаменатель не просто одного порядка роста, а ещё и эквивалентны. На уроке Замечательные пределы. Примеры решений мы без проблем свели данный пример к неопределённости ![]() и получили ответ.
и получили ответ.
Аналогичных пределов можно придумать очень много:
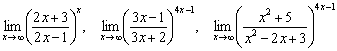 и т. д.
и т. д.
Дроби данных примеров объединяет вышеуказанная особенность: ![]() . В других случаях при неопределённости
. В других случаях при неопределённости ![]() 2-й замечательный предел не применИм.
2-й замечательный предел не применИм.
Пример 21
Найти пределы
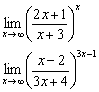
Как ни старайся, а неопределённость ![]() не удастся преобразовать в неопределённость
не удастся преобразовать в неопределённость ![]()
Здесь числители и знаменатели оснований одного порядка роста, но не эквиваленты: ![]() .
.
Таким образом, 2-й замечательный предел и, тем более формулу, ПРИМЕНИТЬ НЕЛЬЗЯ.
! Примечание: не путайте с Примером № 18, в котором числитель и знаменатель основания не эквивалентны. Там готовая неопределённость ![]() , здесь же речь идёт о неопределённости
, здесь же речь идёт о неопределённости ![]() .
.
Метод решения пределов-«подделок» прост и знакОм: нужно числитель и знаменатель основания разделить на «икс» в старшей степени (невзирая на показатель):
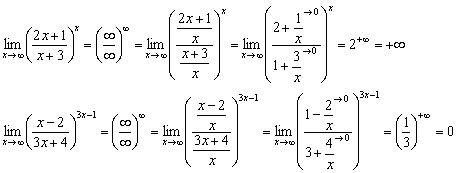
Если числитель и знаменатель основания разного порядка роста, то приём решения точно такой же:
Пример 22
Найти пределы
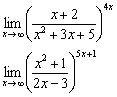
Это короткие примеры для самостоятельного изучения
Иногда неопределённости может не быть вообще:
![]()
Подобные фокусы особенно любимы составителями сборника Кузнецова. Вот почему очень важно ВСЕГДА на первом шаге выполнять подстановку «икса» в выражение под знаком предела!
Завершая тотальное разоблачение пределов, я хочу поздравить всех посетителей сайта с новым 2013 годом! С подарком я успел, и постинг данной статьи осуществлен 31 декабря 2012 года. Вы спросите, а как же моя личная подготовка к празднику? Давно готов =) На протяжении многих лет я занимаюсь стратегическим планированием – чтобы не толкаться в очередях до и не пересекаться с краснокожими после =)
Берегите печень!
Решения и ответы:
Пример 2
![]()
Старшая степень числителя: 2; старшая степень знаменателя: 3.
Разделим числитель и знаменатель на ![]() :
:
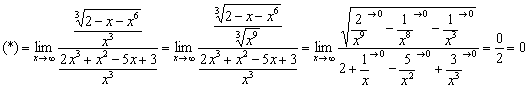
Пример 4
![]()
Разделим числитель и знаменатель на ![]() :
:
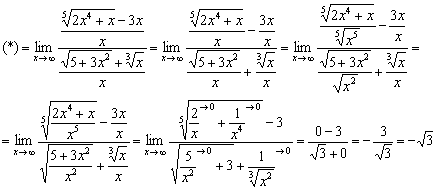
Примечание: самым последним действием умножили числитель и знаменатель на ![]() , чтобы избавиться от иррациональности в знаменателе.
, чтобы избавиться от иррациональности в знаменателе.
Пример 6
![]()
Разделим числитель и знаменатель на ![]() :
:
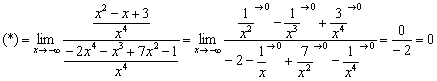
Пример 8
![]()
Разделим числитель и знаменатель на ![]() :
:
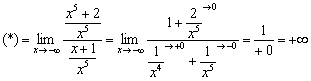
Примечание: слагаемое ![]() стремится к нулю медленнее, чем
стремится к нулю медленнее, чем ![]() , поэтому
, поэтому ![]() является «главным» нулём знаменателя.
является «главным» нулём знаменателя.
Пример 10
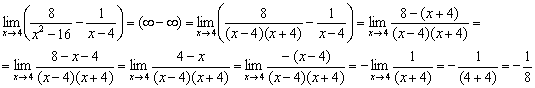
Пример 12
![]()
Умножим и разделим на сопряженное выражение:
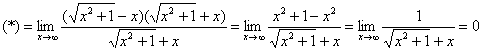
Пример 13
![]()
Умножим и разделим на сопряженное выражение:
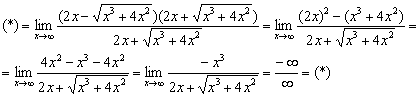
Разделим числитель и знаменатель на ![]() :
:
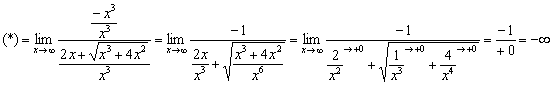
Пример 15
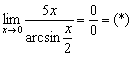
Проведём замену: ![]()
Если ![]() , то
, то ![]() .
.
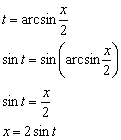
![]()
Пример 17
![]()
Проведём замену: ![]()
Если ![]() , то
, то ![]() .
.
Далее используем формулу приведения ![]() , тригонометрическую формулу
, тригонометрическую формулу ![]() и первый замечательный предел:
и первый замечательный предел:
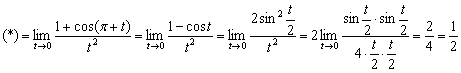
Пример 20
![]()
Используем формулу ![]()
![]()
Пример 22
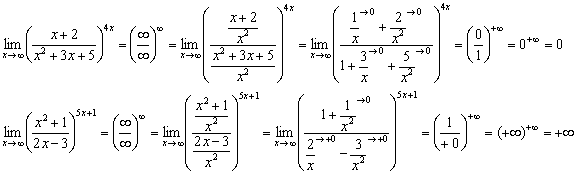
Примечание: бесконечно малая функция ![]() стремится к нулю медленнее, чем
стремится к нулю медленнее, чем ![]() , поэтому «более большой» ноль знаменателя играет определяющую роль:
, поэтому «более большой» ноль знаменателя играет определяющую роль: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright