


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как найти частное решение ДУ приближённо с помощью ряда?
Продолжая изучать практические приложения теории рядов, рассмотрим ещё одну распространённую задачу, название которой вы видите в заголовке. И, чтобы не чувствовать себя газонокосилкой на протяжении урока, давайте сразу же разберёмся в сути задания. Три вопроса и три ответа:
Что нужно найти? Частное решение дифференциального уравнения. Намёк между строк шепчет, что к данному моменту желательно хотя бы понимать, что такое дифференциальное уравнение и что такое его решение.
КАК по условию требуется это решение? Приближённо – с помощью ряда.
И третий закономерный вопрос: почему приближённо? Этот вопрос я уже освещал на уроке Методы Эйлера и Рунге-Кутты, однако повторение не помешает. Будучи сторонником конкретики, вернусь к простейшему дифференциальному уравнению ![]() . В ходе первой лекции по диффурам мы нашли его общее решение
. В ходе первой лекции по диффурам мы нашли его общее решение ![]() (множество экспонент) и частное решение
(множество экспонент) и частное решение ![]() , соответствующее начальному условию
, соответствующее начальному условию ![]() . График функции
. График функции ![]() – это самая обычная линия, которую нетрудно изобразить на чертеже.
– это самая обычная линия, которую нетрудно изобразить на чертеже.
Но то элементарный случай. На практике встречается великое множество дифференциальных уравнений, неразрешимых аналитически точно (по крайне мере, известными на сегодняшний день способами). Иными словами, как ни крути такое уравнение – проинтегрировать его не удастся. А закавыка состоит в том, что общее решение (семейство линий на плоскости) может существовать. И тогда на помощь приходят методы вычислительной математики.
Встречаем нашу радость!
Типовая задача формулируется следующим образом:
Найти приближённо частное решение ![]() дифференциального уравнения …, удовлетворяющее начальному условию
дифференциального уравнения …, удовлетворяющее начальному условию ![]() , в виде трёх (реже – четырёх-пяти) отличных от нуля членов ряда Тейлора.
, в виде трёх (реже – четырёх-пяти) отличных от нуля членов ряда Тейлора.
Искомое частное решение ![]() раскладывается в данный ряд по известной формуле:
раскладывается в данный ряд по известной формуле:
![]()
Единственное, здесь вместо буквы «эф» используется «игрек» (так уж повелось).
Идея и смысл тоже знакомы: для некоторых диффуров и при некоторых условиях (не будем вдаваться в теорию) построенный степенной ряд будет сходиться к искомому частному решению ![]() . То есть чем больше членов ряда мы рассмотрим, тем точнее график соответствующего многочлена приблизит график функции
. То есть чем больше членов ряда мы рассмотрим, тем точнее график соответствующего многочлена приблизит график функции ![]() .
.
Следует отметить, что вышесказанное применимо и к самым простым случаям. Проведём незамысловатое детское исследование на том же горшке:
Пример 1
Найти приближённо частное решение ![]() дифференциального уравнения
дифференциального уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() в виде четырёх первых отличных от нуля членов ряда Тейлора.
в виде четырёх первых отличных от нуля членов ряда Тейлора.
Решение: в условиях данной задачи ![]() , поэтому общая формула Тейлора
, поэтому общая формула Тейлора ![]() трансформируется в частный случай разложения в ряд Маклорена:
трансформируется в частный случай разложения в ряд Маклорена:
![]()
Немного забегая вперёд, скажу, что в практических заданиях значительно чаще встречается именно этот, более компактный ряд.
Занесите обе рабочие формулы в свой справочник.
Разбираемся со значениями ![]() . Этапы решения удобно занумеровать:
. Этапы решения удобно занумеровать:
0) На нулевом шаге записываем значение ![]() , которое всегда известно из условия. В тетради итоговые результаты пунктов желательно обводить в кружок, чтобы они были хорошо видны и не затерялись в решении. Мне по техническим причинам сподручнее выделять их жирным шрифтом. Кроме того, отмечаем, что данное значение не равно нулю! Ведь по условию требуется найти четыре отличных от нуля членов ряда.
, которое всегда известно из условия. В тетради итоговые результаты пунктов желательно обводить в кружок, чтобы они были хорошо видны и не затерялись в решении. Мне по техническим причинам сподручнее выделять их жирным шрифтом. Кроме того, отмечаем, что данное значение не равно нулю! Ведь по условию требуется найти четыре отличных от нуля членов ряда.
1) Вычислим ![]() . Для этого в правую часть исходного уравнения
. Для этого в правую часть исходного уравнения ![]() вместо «игрека» подставляем известное значение
вместо «игрека» подставляем известное значение ![]() :
:
![]()
2) Вычислим ![]() . Сначала находим вторую производную:
. Сначала находим вторую производную:
![]()
Подставляем в правую часть найдённое в предыдущем пункте значение ![]() :
:
![]()
В распоряжении уже три ненулевых члена разложения, нужен ещё один:
3) Находим третью производную – это производная от второй производной:
![]()
Так получается, что в данном задании каждая следующая производная оказывается выраженной через предыдущую производную.
Подставляем в правую часть найденное в предыдущем пункте значение ![]() :
:
![]()
Теперь подставим найденные значения в формулу Маклорена и аккуратно проведём упрощения:
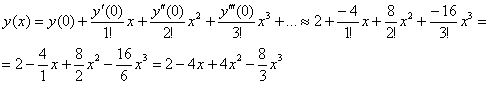
Ответ: ![]()
Условие рассматриваемого задания, как правило, не требует чертежа, но я построю демонстрационные графики, чтобы наглядно разъяснить сущность выполненных действий. Изобразим точное частное решение ![]() и его приближение
и его приближение ![]() :
:
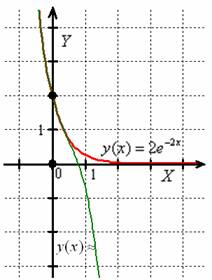
Как видите, уже 4 члена ряда дают недурственную точность – на довольно длинном участке зелёная дуга кубической функции практически совпала с идеальным («красным») решением, о чём нам сигнализирует коричневый цвет. При этом оба графика проходят через точку начального условия, и естественно, что вблизи неё точность будет максимальной.
Очевидно, что чем больше членов ряда мы рассмотрим, тем лучше соответствующий многочлен приблизит экспоненту.
Неудивительно, что в решении часто задействованы производные более высоких порядков. Кратко повторим материал:
четвёртая производная ![]() – это производная от третьей производной;
– это производная от третьей производной;
пятая производная ![]() – это производная от четвёртой производной и т. д.;
– это производная от четвёртой производной и т. д.;
![]() – обозначения 6-й, 7-й, 8-й, 9-й и 10-й производных соответственно.
– обозначения 6-й, 7-й, 8-й, 9-й и 10-й производных соответственно.
Помимо римских цифр, в широком обиходе и такой вариант:
![]() – обязательно со скобками, чтобы не путать производную с «игреком в степени».
– обязательно со скобками, чтобы не путать производную с «игреком в степени».
В собственной практике приходилось находить 10-ю производную, не случайно я так подробно воспроизвёл обозначения.
Для успешного выполнения данной задачи необходимо уметь дифференцировать неявную функцию, причём дифференцировать достаточно уверенно. И, прежде чем перейти к конкретным примерам, пожалуйста, проанализируйте, понятны ли вам следующие производные:
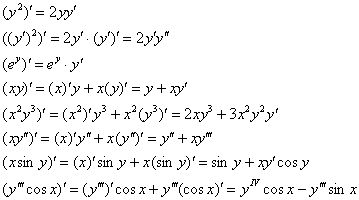
Если не очень, то лучше проработать примеры урока о производных неявно заданных функций. Также проблема может быть в позабытых правилах дифференцирования. В частности, только что и далее будут широко применяться правило дифференцирования произведения ![]() и правило дифференцирования сложной функции
и правило дифференцирования сложной функции ![]() Пожалуй, некоторая новизна лишь в производной
Пожалуй, некоторая новизна лишь в производной ![]() (вторая строка), где в качестве внешней функции выступает степень (квадрат), а в качестве вложения – производная
(вторая строка), где в качестве внешней функции выступает степень (квадрат), а в качестве вложения – производная ![]() .
.
Алгоритм и технику решения начнём оттачивать с общего случая разложения в ряд Тейлора:
Пример 2
Найти приближённо частное решение ![]() дифференциального уравнения
дифференциального уравнения ![]() , удовлетворяющее начальному условию
, удовлетворяющее начальному условию ![]() в виде трёх первых отличных от нуля членов ряда Тейлора.
в виде трёх первых отличных от нуля членов ряда Тейлора.
Решение начинается стандартной фразой:
Разложение частного решения ![]() дифференциального уравнения при начальном условии
дифференциального уравнения при начальном условии ![]() имеет вид:
имеет вид:
![]()
В данной задаче ![]() , следовательно:
, следовательно:
![]()
Теперь последовательно находим значения ![]() – до тех пор, пока не будут получены три ненулевых результата. Если повезёт, то отличны от нуля будут
– до тех пор, пока не будут получены три ненулевых результата. Если повезёт, то отличны от нуля будут ![]() – это идеальный случай с минимальным количеством работы.
– это идеальный случай с минимальным количеством работы.
Нарезаем пункты решения:
0) По условию ![]() . Вот и первый успех.
. Вот и первый успех.
1) Вычислим ![]() . Сначала разрешим исходное уравнение относительно первой производной, то есть выразим
. Сначала разрешим исходное уравнение относительно первой производной, то есть выразим ![]() . Подставим в правую часть известные значения
. Подставим в правую часть известные значения ![]() :
:
![]()
Получена баранка и это не есть хорошо, поскольку нас интересуют ненулевые значения. Однако ноль – тоже результат, который не забываем обвести в кружок или выделить каким-нибудь другим способом.
2) Находим вторую производную ![]() и подставляем в правую часть известные значения
и подставляем в правую часть известные значения ![]() :
:
![]()
Второй «не ноль».
3) Находим ![]() – производную от второй производной:
– производную от второй производной:
![]()
Если действия не понятны, ещё раз призываю изучить статью о дифференцировании неявной функции.
Вообще, задание чем-то напоминает Сказку про Репку, когда дедка, бабка и внучка зовут на помощь жучку, кошку и т. д. И в самом деле, каждая следующая производная выражается через своих «предшественников».
Подставим в правую часть ![]() известные значения
известные значения ![]() :
:
![]()
Третье ненулевое значение. Вытащили Репку.
Аккуратно и внимательно подставляем «жирные» числа в нашу формулу:
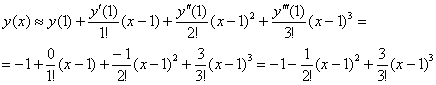
Ответ: искомое приближенное разложение частного решения: ![]()
В рассмотренном примере попался всего один ноль на втором месте, и это не так уж плохо. В общем случае нулей может встретиться сколько угодно и где угодно. Повторюсь, их очень важно выделять наряду с ненулевыми результатами, чтобы не запутаться в подстановках на завершающем этапе.
Вот, пожалуйста – бублик на самом первом месте:
Пример 3
Найти приближённо частное решение дифференциального уравнения ![]() , соответствующее начальному условию
, соответствующее начальному условию ![]() , в виде трёх первых отличных от нуля членов ряда Тейлора.
, в виде трёх первых отличных от нуля членов ряда Тейлора.
Примерный образец оформления задачи в конце урока. Пункты алгоритма можно и не нумеровать (оставляя, например, пустые строки между шагами), но начинающим рекомендую придерживаться строгого шаблона.
Рассматриваемая задача требует повышенного внимания – если допустить ошибку на каком-либо шаге, то всё остальное тоже будет неверным! Поэтому ваша ясная голова должна работать как часы. Увы, это не интегралы или диффуры, которые надёжно решаются и в утомлённом состоянии, поскольку позволяют выполнить эффективную проверку.
На практике заметно чаще встречается разложение в ряд Маклорена:
Пример 4
Представить приближенно частное решение ![]() ДУ, соответствующее заданному начальному условию
ДУ, соответствующее заданному начальному условию ![]() , в виде суммы трех первых отличных от нуля членов степенного ряда.
, в виде суммы трех первых отличных от нуля членов степенного ряда.
![]()
Решение: в принципе, можно сразу записать разложение Маклорена, но оформление задачи академичнее начать с общего случая:
Разложение частного решения ![]() дифференциального уравнения при начальном условии
дифференциального уравнения при начальном условии ![]() имеет вид:
имеет вид:
![]()
В данном случае ![]() , следовательно:
, следовательно:
![]()
Вперёд:
0) По условию ![]() .
.
Ну что поделать…. Будем надеяться, что нулей встретится поменьше.
1) Вычислим ![]() . Первая производная
. Первая производная ![]() уже готова к употреблению. Подставим значения
уже готова к употреблению. Подставим значения ![]() :
:
![]()
2) Найдём вторую производную:
![]()
И подставим в неё ![]() :
:
![]()
Резво дело пошло!
3) Находим ![]() . Распишу очень подробно:
. Распишу очень подробно:
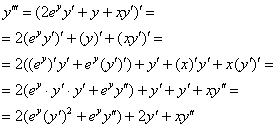
Заметьте, что к производным применимы обычные алгебраические правила: приведение подобных слагаемых ![]() на последнем шаге и запись произведения в виде степени:
на последнем шаге и запись произведения в виде степени: ![]() (там же).
(там же).
Подставим в ![]() всё, что нажито непосильным трудом
всё, что нажито непосильным трудом ![]() :
:
![]()
Три ненулевых значения рождены.
Подставляем «жирные» числа в формулу Маклорена, получая тем самым приближенное разложение частного решения:
![]()
Ответ: ![]()
Для самостоятельного решения:
Пример 5
Представить приближенно частное решение ![]() ДУ, соответствующее заданному начальному условию
ДУ, соответствующее заданному начальному условию ![]() , в виде суммы трех первых отличных от нуля членов степенного ряда.
, в виде суммы трех первых отличных от нуля членов степенного ряда.
![]()
Примерный образец оформления в конце урока.
Как видите, задача с частным разложением в ряд Маклорена оказалась даже труднее общего случая. Сложность рассматриваемого задания, как мы только что убедились, состоит не столько в самом разложении, сколько в трудностях дифференцирования. Более того, порой, приходится находить 5-6 производных (а то и больше), что повышает риск ошибки. И в завершении урока предлагаю пару задач повышенной сложности:
Пример 6
Решить дифференциальное уравнение приближённо с помощью разложения частного решения в ряд Маклорена, ограничившись тремя первыми ненулевыми членами ряда
![]()
Решение: перед нами диффур второго порядка, но это практически не меняет дела. По условию ![]() и нам сразу же предложено воспользоваться рядом Маклорена, чем мы не преминем воспользоваться. Запишем знакомое разложение, прихватив на всякий пожарный побольше слагаемых:
и нам сразу же предложено воспользоваться рядом Маклорена, чем мы не преминем воспользоваться. Запишем знакомое разложение, прихватив на всякий пожарный побольше слагаемых:
![]()
Алгоритм работает точно так же:
0) ![]() – по условию.
– по условию.
1) ![]() – по условию.
– по условию.
2) Разрешим исходное уравнение относительно второй производной: ![]() .
.
И подставим ![]() :
:
![]()
Первое ненулевое значение
Щёлкаем производные и выполняем подстановки:
3) ![]()
Подставим ![]() и
и ![]() :
:
![]()
4) ![]()
Подставим ![]() :
:
![]()
Второе ненулевое значение.
5) ![]() – по ходу дела приводим подобные производные.
– по ходу дела приводим подобные производные.
Подставим ![]() :
:
![]()
6) ![]()
Подставим ![]() :
:
![]()
Наконец-то. Впрочем, бывает и хуже.
Таким образом, приближенное разложение искомого частного решения:
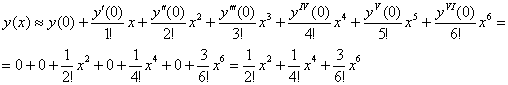
Ответ: ![]()
Миниатюра для самостоятельного решения:
Пример 7
Найти три отличных от нуля члена разложения в ряд Маклорена частного решения дифференциального уравнения второго порядка ![]() при начальных условиях
при начальных условиях ![]() .
.
Я хочу, чтобы все читатели решили это задание. Ведь курс математического анализа потихоньку заканчивается…,. пройдут годы, но когда-нибудь каждого из вас посетит непреодолимое желание что-нибудь продифференцировать. Поэтому не упускайте редкую возможность начать прямо сейчас =)
Решения и ответы:
Пример 3. Решение: разложение частного решения ![]() ДУ при начальном условии
ДУ при начальном условии ![]() имеет вид:
имеет вид: ![]() .
.
В данном случае: ![]() .
.
В правую часть ![]() подставим
подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Таким образом, искомое приближенное разложение частного решения:
![]()
Ответ: ![]()
Пример 5. Решение: разложение частного решения ![]() ДУ при начальном условии
ДУ при начальном условии ![]() имеет вид:
имеет вид: ![]() .
.
В данном случае ![]() , следовательно:
, следовательно:
![]()
![]() .
.
Разрешим исходное уравнение относительно ![]() .
.
Подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Найдём третью производную:
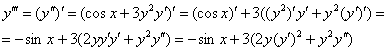
Подставим ![]() :
: ![]()
![]()
Таким образом, искомое приближенное разложение частного решения:
![]()
Ответ: ![]()
Пример 7. Решение: используем разложение Маклорена:
![]()
По условию:
![]()
![]()
В исходное уравнение ![]() подставим
подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Найдём ![]()
Подставим ![]() :
:
![]()
Таким образом, приближенное разложение искомого частного решения:
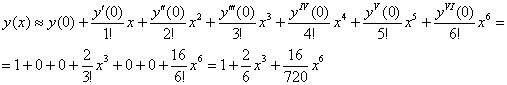
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright