Предел последовательности и предел функции по Коши

Сегодня на уроке мы разберём строгое определение последовательности и строгое определение предела функции, а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т. п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна. И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется ;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!) о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)

– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ~~ноги~~ руку помощи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций, в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей, на котором я фактически уже сформулировал строгое определение.

На начальном этапе не рекомендую особо заглядывать в учебник по математическому анализу, да и в собственные записи тоже. Хотя давайте немного причастимся:

Какие значки помимо знаков неравенств и модуля вы знаете?

Из курса алгебры нам известны следующие обозначения:

– квантор всеобщности обозначает– «для любого», «для всех», «для каждого», то есть запись следует прочитать «для любого положительного эпсилон»;

– квантор существования, – существует значение , принадлежащее множеству натуральных чисел.

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что», в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;

– для всех «эн», бОльших чем ;

– знак модуля означает расстояние, т. е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.

А теперь попытайтесь прочитать строку целиком.

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

Определение предела последовательности

И в самом деле, немного порассуждаем – как сформулировать строгое определение последовательности? …Первое, что приходит на ум в свете практического занятия: «предел последовательности – это число, к которому бесконечно близко приближаются члены последовательности».

Хорошо, распишем последовательность :

Нетрудно уловить, что подпоследовательность бесконечно близко приближаются к числу –1, а члены с чётными номерами – к «единице».

А может быть предела два? Но тогда почему у какой-нибудь последовательности их не может быть десять или двадцать? Так можно далеко зайти. В этой связи логично считать, что если у последовательности существует предел, то он единственный.

Примечание: у последовательности нет предела, однако из неё можно выделить две подпоследовательности (см. выше), у каждой из которых существует свой предел.

Таким образом, высказанное выше определение оказывается несостоятельным. Да, оно работает для случаев вроде (чем я не совсем корректно пользовался в упрощённых объяснениях практических примеров), но сейчас нам нужно отыскать строгое определение.

Попытка вторая: «предел последовательности – это число, к которому приближаются ВСЕ члены последовательности, за исключением, разве что их конечного количества». Вот это уже ближе к истине, но всё равно не совсем точно. Так, например, у последовательности половина членов вовсе не приближается к нулю – они ему просто-напросто равны =) К слову, «мигалка» вообще принимает два фиксированных значения.

Формулировку нетрудно уточнить, но тогда возникает другой вопрос: как записать определение в математических знаках? Научный мир долго бился над этой проблемой, пока ситуацию не разрешил известный маэстро, который, по существу, и оформил классический матанализ во всей его строгости. Коши предложил оперировать окрестностями, чем значительно продвинул теорию.

Рассмотрим некоторую точку и её произвольную -окрестность:
Определение предела последовательности
Значение «эпсилон» всегда положительно, и, более того, мы вправе выбрать его самостоятельно. Предположим, что в данной окрестности находится множество членов (не обязательно все) некоторой последовательности . Как записать тот факт, что, например десятый член попал в окрестность? Пусть он находится в правой её части. Тогда расстояние между точками и должно быть меньше «эпсилон»: . Однако если «икс десятое» расположено левее точки «а», то разность будет отрицательна, и поэтому к ней нужно добавить знак модуля: .

Определение: число называется пределом последовательности, если для любой его окрестности (заранее выбранной) существует натуральный номер – ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерами окажутся внутри окрестности:

Или короче: , если

Из чего следует, что какое бы малое значение «эпсилон» мы ни взяли, рано или поздно «бесконечный хвост» последовательности ПОЛНОСТЬЮ окажется в этой окрестности.

Так, например, «бесконечный хвост» последовательности ПОЛНОСТЬЮ зайдёт в любую сколь угодно малую -окрестность точки . Таким образом, это значение является пределом последовательности по определению. Напоминаю, что последовательность, предел которой равен нулю, называют бесконечно малой.

Следует отметить, что для последовательности уже нельзя сказать «бесконечный хвост зайдёт» – члены с нечётными номерами по факту равны нулю и «никуда не заходят» =) Именно поэтому в определении использован глагол «окажутся». И, разумеется, члены такой последовательности, как тоже «никуда не идут». Кстати, проверьте, будет ли число её пределом.

Теперь покажем, что у последовательности не существует предела. Рассмотрим, например, окрестность точки . Совершенно понятно, что нет такого номера, после которого ВСЕ члены окажутся в данной окрестности – нечётные члены всегда будут «выскакивать» к «минус» единице. По аналогичной причине не существует предела и в точке .

Начинающим рекомендую 2-3 раза перечитать вышесказанное + параграф понятие предела последовательности предыдущего урока, где я объяснил то же самое, но без математических значков.

Закрепим материал практикой:

Пример 1

Доказать что предел последовательности равен нулю. Указать номер , после которого, все члены последовательности гарантированно окажутся внутри любой -окрестности точки .

Примечание: у многих последовательностей искомый натуральный номер зависит от значения – отсюда и обозначение .

Решение: рассмотрим произвольную -окрестность точки и проверим, найдётся ли номер – такой, что ВСЕ члены с бОльшими номерами окажутся внутри этой окрестности:

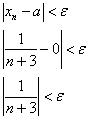
Чтобы показать существование искомого номера , выразим через .

Так как при любом значении «эн» , то знак модуля можно убрать:

Используем «школьные» действия с неравенствами, которые я повторял на уроках Линейные неравенства и Область определения функции. При этом важным обстоятельством является то, что «эпсилон» и «эн» положительны:

Поскольку слева речь идёт о натуральных номерах, а правая часть в общем случае дробна, то её нужно округлить:

Примечание: иногда для перестраховки справа добавляют единицу, но на самом деле это излишество. Условно говоря, если и мы ослабим результат округлением в меньшую сторону , то ближайший подходящий номер («тройка») всё равно будет удовлетворять первоначальному неравенству.

А теперь смотрим на неравенство и вспоминаем, что изначально мы рассматривали произвольную -окрестность, т. е. «эпсилон» может быть равно любому положительному числу.

Если выбранная окрестность достаточно великА, то в правой части неравенства мы получим ноль или даже отрицательное значение, в этом случае все члены последовательности войдут в -окрестность с первого же номера.

Если же «эпсилон» достаточно малО, то для любой сколь угодно малой -окрестности точки найдётся натуральное значение , такое, что для всех бОльших номеров выполнено неравенство .

Вывод: число является пределом последовательности по определению. Что и требовалось доказать.

К слову, из полученного результата хорошо просматривается естественная закономерность: чем меньше -окрестность – тем больше номер , после которого ВСЕ члены последовательности окажутся в данной окрестности. Но каким бы малым ни было «эпсилон» – внутри всегда будет «бесконечный хвост», а снаружи – пусть даже большое, однако конечное число членов.

Как впечатления? =) Согласен, что странновато. Но строго! Пожалуйста, перечитайте и осмыслите всё ещё раз.

Рассмотрим аналогичный пример и познакомимся с другими техническими приёмами:

Пример 2

Используя определение последовательности, доказать, что

Решение: по определению последовательности нужно доказать, что (проговариваем вслух!!!).

Рассмотрим произвольную -окрестность точки и проверим, существует ли натуральный номер – такой, что для всех бОльших номеров выполнено неравенство:

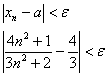
Чтобы показать существование такого , нужно выразить «эн» через «эпсилон». Упрощаем выражение под знаком модуля:

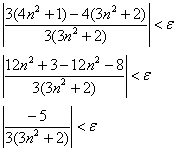
Модуль уничтожает знак «минус»:

Знаменатель положителен при любом «эн», следовательно, палки можно убрать:

Перетасовка:

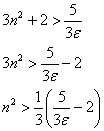
Теперь надо бы извлечь квадратный корень, но загвоздка состоит в том, что при достаточно больших «эпсилон» правая часть будет отрицательной. Чтобы избежать этой неприятности усилим неравенство модулем:

Почему так можно сделать? Если, условно говоря, окажется, что , то подавно будет выполнено и условие . Модуль может только увеличить разыскиваемый номер , и это нас тоже устроит! Грубо говоря, если подходит сотый, то подойдёт и двухсотый! В соответствии с определением, нужно показать сам факт существования номера (хоть какого-то), после которого все члены последовательности окажутся в -окрестности. Кстати, именно поэтому нам не страшнО финальное округление правой части неравенства в бОльшую сторону (а в предыдущем примере мы, к слову, могли заключить правую часть ещё и в модуль).

Извлекаем корень:

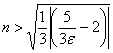
И округляем результат:

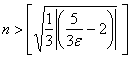
Вывод: т. к. значение «эпсилон» выбиралось произвольно, то для любой -окрестности точки нашлось значение 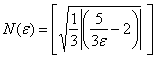, такое, что для всех бОльших номеров выполнено неравенство 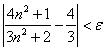. Таким образом, по определению. Что и требовалось доказать.

Советую особо разобраться в усилении и ослаблении неравенств – это типичные и очень распространённые приёмы математического анализа. Единственное, нужно следить за корректностью того или иного действия. Так, например, неравенство ни в коем случае нельзя ослаблять, вычитая, скажем, единицу:

Опять же условно: если номер точно подойдёт, то предыдущий может уже и не подойти.

Следующий пример для самостоятельного решения:

Пример 3

Используя определение последовательности, доказать, что

Краткое решение и ответ в конце урока.

Если последовательность бесконечно велика, то определение предела формулируется похожим образом: точка называется пределом последовательности, если для любого, сколь угодно большого числа существует номер , такой, что для всех бОльших номеров , будет выполнено неравенство . Число называют окрестностью точки «плюс» бесконечность:
Определение предела бесконечно большой последовательности

Иными словами, какое бы большое значение мы ни взяли, «бесконечный хвост» последовательности обязательно зайдёт в -окрестность точки , оставив слева лишь конечное число членов.

Дежурный пример:

И сокращённая запись: , если

Для случая запишите определение самостоятельно. Правильная версия в конце урока.

После того, как вы «набили» руку на практических примерах и разобрались с определением предела последовательности, можно обратиться к литературе по математическому анализу и/или своей тетрадке с лекциями. Рекомендую закачать 1-й том Бохана (попроще – для заочников) и Фихтенгольца (более подробно и обстоятельно). Из других авторов советую Пискунова, курс которого ориентирован на технические ВУЗы.

Попытайтесь добросовестно изучить теоремы, которые касаются предела последовательности, их доказательства, следствия. Поначалу теория может казаться «мутной», но это нормально – просто нужно привыкнуть. И многие даже войдут во вкус!

Строгое определение предела функции

Начнём с того же самого – как сформулировать данное понятие? Словесное определение предела функции формулируется значительно проще: «число является пределом функции , если при «икс», стремящемся к (и слева, и справа), соответствующие значения функции стремятся к » (см. чертёж). Всё вроде бы нормально, но слова словами, смысл смыслом, значок значком, а строгих математических обозначений маловато. И во втором параграфе мы познакомимся с двумя подходами к решению данного вопроса.

Пусть функция определена на некотором промежутке за исключением, возможно, точки . В учебной литературе общепринято считают, что функция там не определена:
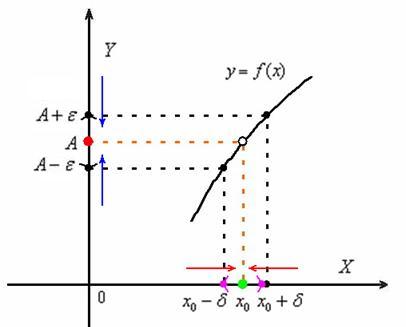
Определение предела функции по Коши

Такой выбор подчёркивает суть предела функции: «икс» бесконечно близко приближается к , и соответствующие значения функции – бесконечно близко к (в некоторых частных случаях значение имеется по факту либо достигается). Иными словами, понятие предела подразумевает не «точный заход» в точки, а именно бесконечно близкое приближение, при этом не важно – определена ли функция в точке или нет.

Первое определение предела функции, что неудивительно, формулируется с помощью двух последовательностей. Во-первых, понятия родственные, и, во-вторых, пределы функций обычно изучают после пределов последовательностей.

Рассмотрим последовательность точек (на чертеже отсутствуют), принадлежащих промежутку и отличных от , которая сходится к . Тогда соответствующие значения функции тоже образуют числовую последовательность, члены которой располагаются на оси ординат.

Предел функции по Гейне: число называется пределом функции в точке , если для любой последовательности точек (принадлежащих и отличных от ), которая сходится к точке , соответствующая последовательность значений функции сходится к .

Эдуард Гейне – это немецкий математик. …И не надо тут ничего такого думать, гей в Европе всего лишь один – это Гей-Люссак =)

Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность). По мотивам предыдущего параграфа, запись означает, что некоторое значение функции находится внутри «эпсилон»-окрестности.

Теперь найдём -окрестность, которая соответствует заданной -окрестности (мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз). Обратите внимание, что значение выбирается по длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определении важен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.

Предел функции по Коши: число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой), существует -окрестность точки , ТАКАЯ, что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки).

Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

Короткая запись: , если

В чём суть определения? Образно говоря, бесконечно уменьшая -окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.

! Внимание: если вам потребуется сформулировать только определение по Гейне или только определение по Коши, пожалуйста, не забывайте о существенном предварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки ». Я обозначил это единожды в самом начале и каждый раз не повторял.

Согласно соответствующей теореме математического анализа, определения по Гейне и по Коши эквивалентны, однако наиболее известен второй вариант (ещё бы!), который также называют «предел на языке »:

Пример 4

Используя определение предела, доказать, что

Решение: функция определена на всей числовой прямой кроме точки . Используя определение , докажем существование предела в данной точке.

Примечание: величина «дельта»-окрестности зависит от «эпсилон», отсюда и обозначение

Рассмотрим произвольную -окрестность. Задача состоит в том, чтобы по этому значению проверить, существует ли -окрестность, ТАКАЯ, что из неравенства следует неравенство .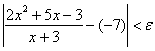

Предполагая, что , преобразуем последнее неравенство:
(разложили квадратный трёхчлен)

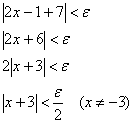
После упрощений для лучшего понимания перепишем ещё раз то, что требовалось проверить: «…существует ли -окрестность, ТАКАЯ что из неравенства следует неравенство ?»

Конечно, существует, например, . В этом случае из неравенства следует (формально оно же само). Следует отметить, что в качестве примера можно привести и любую меньшую «дельта»-окрестность, например, , поскольку из неравенства тем более следует, что (из того, что «в кармане меньше 50 рублей» следует то, что «в кармане меньше 100 рублей»). Однако в качестве стандартного примера окрестности практически всегда берут «пограничное» значение, в данном примере .

Вывод: для любой, сколько угодно малой -окрестности точки нашлась окрестность точки , такая, что из неравенства следует неравенство 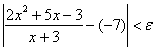. Таким образом, по определению предела функции. Ч. т. д.

Небольшое задание для самостоятельного решения.

Пример 5

Доказать, что

Слишком просто? А вы попробуйте грамотно оформить, и, самое главное, ПОНЯТЬ, ход решения ;-)

Следует отметить, что рассмотренные задачи не дают нам каких-то способов решения пределов, они позволяют лишь доказать либо опровергнуть существование некоторых из них.

Определение бесконечного предела, в частности предела , тоже формулируется двумя способами. Приведу наиболее популярный вариант. Пусть функция определена на промежутке , который содержит сколь угодно большие значения «икс». Предел функции равен «плюс» бесконечности при , если для любого сколь угодно большого числа (заранее заданного) найдётся окрестность , такая, что: КАК ТОЛЬКО значения аргумента войдут в данную окрестность: (красная стрелка), ТАК СРАЗУ соответствующие значения функции зайдут в -окрестность: (синяя стрелка):
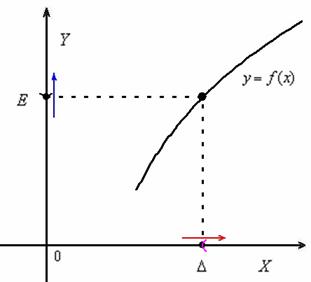
Определение бесконечного предела функции
Сокращённая запись: , если

Определения следующих двух пределов предлагаю сформулировать самостоятельно:

Изобразите на чертеже принципиальную картину, прорисуйте окрестности и постарайтесь корректно записать определения. Для обозначения закрытых окрестностей используйте буквы , для открытых к бесконечности – буквы . Ответы в конце урока.

Случаи «минус» бесконечности и обобщённый случай легко отыскать в соответствующей литературе.

Что делать дальше? После освоения теории пределов целесообразно перейти к изучению непрерывности функции, правда, в рамках сайта сформулировано лишь «прикладное» определение непрерывности, поэтому книги в помощь. Далее в 1-м семестре, как правило, проходят производные. Здесь я рекомендую придерживаться той же схемы – сначала учимся дифференцировать, затем осваиваем теоретический материал о производной, «сопутствующие» теоремы и т. д.

Ни в коем случае не расстраивайтесь, если дела «пойдут не очень», в конце концов, тут нужно принять во внимание, что учиться на «технаря» вообще непросто: что-то даётся легче, что-то труднее, а с чем-то может и помучиться придётся. Лично у меня некоторые разделы математики шли лучше, некоторые хуже, а программирование вообще переносилось с трудом (уж не знаю, почему). Нельзя идеально знать и любить всё.

Оглядываясь в прошлое, с улыбкой вспоминаю свои первый месяцы учёбы – тогда математический анализ показался мне самой трудной дисциплиной, и я с перепуга выучил ВЕСЬ материал 1-го семестра, даже сказать точнее не выучил, а почти во всём разобрался, чего и всем желаю!

Надеюсь, данная статья была полезна, а может, и послужила ключом к предмету!

Решения и ответы:

Пример 3. Решение: докажем, что . Для этого рассмотрим произвольную -окрестность точки и проверим, найдётся ли натуральный номер – такой, что выполнено:

Преобразуем неравенство:

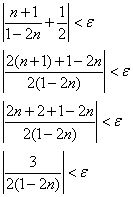
(подумайте, почему)
Для всех «эн»: , поэтому:

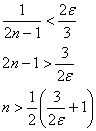
Вывод: т. к. «эпсилон» выбиралось произвольно, то для любой сколько угодно малой -окрестности точки нашлось значение , такое, что выполнено . Таким образом, по определению. Что и требовалось доказать.

Формулировка предела:
, если

Пример 5. Решение: функция определена на всей числовой прямой. Используя определение , докажем существование предела в точке .
Рассмотрим произвольную -окрестность и проверим, найдётся ли -окрестность, такая что из неравенства следует .
Преобразуем неравенство с «эпсилон»:

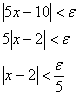
В качестве искомой окрестности выбираем .
Вывод: для любой, сколь угодно малой -окрестности точки нашлось значение , такое, что , следовательно, по определению. Ч. т. д.