Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

17. Комбинационная группировка

На предыдущем уроке мы освоили аналитическую группировку (обязательно к изучению!), и сейчас на очереди ещё один распространённый способ группировки данных.

Комбинационная группировка – это группировка статистической совокупности совместно по двум или бОльшему количеству признаков. Она позволяет выявить устройство совокупности и установить взаимосвязи между её признаками.

Рассмотрим выборку, состоящую из  котов, среди которых оказалось 20 грациозных (менее 4 кг), 50 обычных (4-6 кг) и 30 толстых (более 6 кг). По существу, перед нами структурная группировка животных по их массе и это первый признак статической совокупности. Теперь возьмём какой-нибудь второй признак, например, разделим всех котов на злых и добрых :) Признак, кстати, качественный, но при желании его можно «оцифровать», рассмотрев некую экспертную шкалу доброты.

В результате исследования выяснилось, что среди тощих котов 14 злых и 6 добрых, среди обычных – 24 злых и 26 добрых и среди толстых  – 7 злых и 23 добрых.

Очевидно, что между рассмотренными признаками есть взаимосвязь. Чем больше масса кота, тем более вероятно, что он окажется добрым. Ибо с лишним весом, полным желудком и отрезанн… злиться весьма проблематично. Однако и среди толстых котов тоже есть особи с проблемным характером. Такая нежёсткая зависимость называется…, вспоминаем… – правильно! Корреляционной.

Результаты комбинационной группировки обычно сводят в комбинационную таблицу:

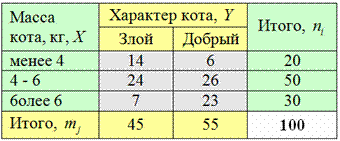
Внимательно изучаем таблицу и обозначения! Это очень, ОЧЕНЬ важно для практики:

! Если вы что-то не очень поняли, ещё раз ВДУМЧИВО перечитайте объяснения!

Может ли в комбинационной группировке быть бОльшее количество факторов? Легко. Так, в нашем примере можно добавить фактор  – жилищные условия кота (бездомный или домашний). В результате получится трёхмерная комбинационная группировка с группами:

тощие, злые и бездомные коты;
тощие, злые и домашние коты;
тощие, добрые и бездомные коты;
тощие, добрые и домашние коты;
обычные, злые и бездомные коты;
…
и так далее, всего 12 групп. Самостоятельно перечислите и представьте все остальные семейства – целый мир получится!

И, завершая занимательное котоведение, призываю вас не кастрировать своих (и чужих) котов. И мир станет гармоничнее! …Простите за лирическое отступление, Майкл Джексон любил детей, а я люблю котов :) Да и студентов тоже не тяну за хвосты :)

Поэтому переходим к стандартным студенческим задачам, в которых предлагается простейшая двумерная комбинационная группировка:

Пример 63

Имеются выборочные данные о выпуске продукции (млн. руб.) и сумме прибыли (млн. руб.) по 30 предприятиям:

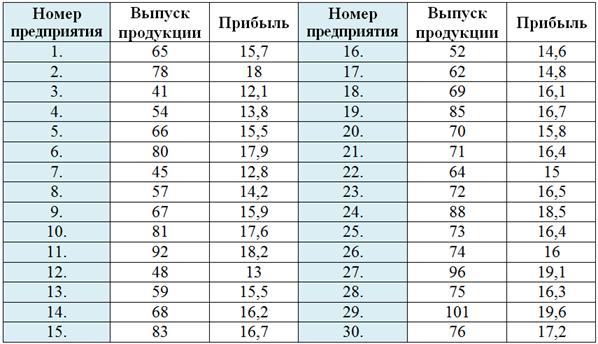
Определить признак-фактор и признак-результат и высказать предположение о наличии и направлении корреляционной зависимости между признаками. Выполнить комбинационную группировку, разбив значения признака-фактора на 5 равных интервалов, а значения признака-результата – на 3 равных интервала. Сделать выводы.

Решение: числовые данные я взял из Примера 61, и если вы с ним не знакомы, то срочно навёрстываем упущенное! В той задаче мы выяснили, что признаком-фактором (причиной) является  – выпуск продукции, а признаком-результатом (следствием)  – прибыль. При увеличении выпуска продукции, очевидно, растёт средняя прибыль предприятий, таким образом, предполагаемая корреляционная зависимость – прямая («чем больше, тем больше»). И снова подчёркиваю нежёсткость этой зависимости: отдельно взятое предприятие может выпускать много, но сидеть в убытках, и наоборот – есть предприятия с небольшим объёмом выпуска, но высокой прибылью. Однако это всё отклонения от общей тенденции.

Выполним комбинационную группировку, разбив значения признака-фактора на 5 равных интервалов, а значения признака-результата – на 3.

Начало решения совпадает с началом Примера 61. Упорядочим предприятия по возрастанию признака-фактора:

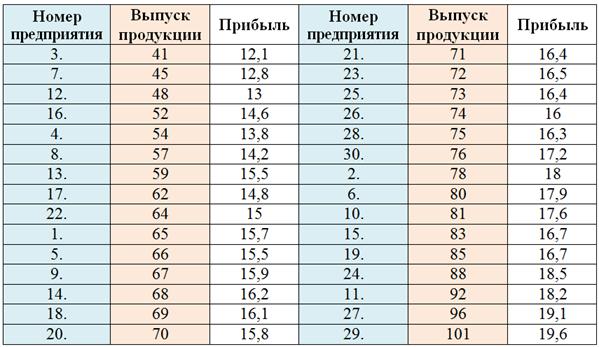
О том, как это быстро сделать в Экселе, есть видео!

Далее мы нашли размах вариации  млн. руб. и длину каждого интервала  млн. руб., после чего у нас получилось 5 групп предприятий:

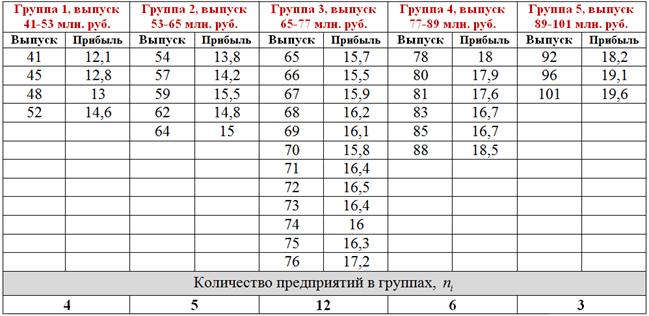
Теперь в каждой группе нужно выделить подгруппы, условно говоря, предприятия с небольшой, средней и высокой прибылью (3 интервала по условию). Для этого берём исходные значения признака-результата (прибыли) и сортируем их по возрастанию. Для компактности расположу упорядоченные значения в три колонки:

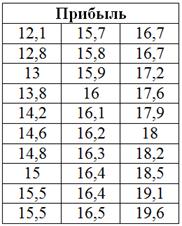
С простейшей экселевской сортировкой, полагаю, проблем уже ни у кого нет. А если таки есть, то гляньте, например, тут. Я зануда, в полезном смысле этого слова :)

Вычислим размах вариации:  млн. руб. и длину каждого интервала: ,… ай, как удачно разделилось! В результате получилось три интервала прибыли: 12,1-14,6; 14,6-17,1 и 17,1-19,6 млн. руб.

Теперь в групповой таблице красными галочками помечаем предприятия 1-го интервала, зелёными – предприятия 2-го интервала и синими – 3-го интервала:

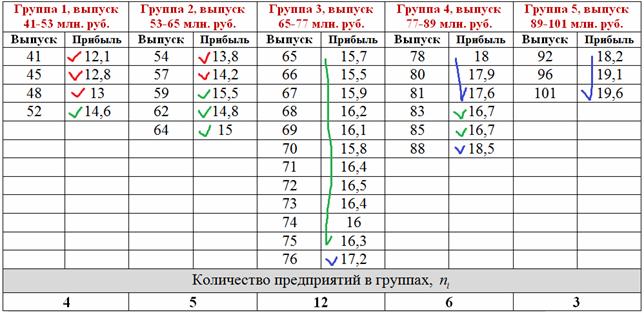
По каждой из 5 групп подсчитываем количество предприятий с небольшой (красной), средней (зелёной) и высокой (синей) прибылью. Результаты сведём в комбинационную таблицу, при этом значения признака-фактора удобно расположить по горизонтали в «шапке» таблицы, а значения признака-результата – слева по вертикали:


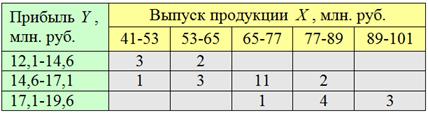
Следует заметить, что построение комбинационной группировки можно автоматизировать (например, в MS Excel), но в простейших учебных примерах проще выполнить ручной подсчёт частот.

Да, всем ли понятны значения (частоты) в серой области? Частота  означает, что у нас есть два предприятия  с выпуском продукции 53-65 млн. руб. и невысокой прибылью (12,1-14,6 млн. руб.). Частота  означает, что в выборке четыре предприятия  с выпуском продукции 77-89 млн. руб. и высокой прибылью (17,1-19,6 млн. руб.).

Для самоконтроля подсчитываем суммы по серым столбцам:  , , всего:  предприятий. Результаты заносим в нижнюю строку (см. таблицу ниже).

И самое интересное – суммы по серым строкам:
 предприятий с небольшой прибылью;
 предприятий со средней прибылью;
 предприятий с высокой прибылью.

Всего: , что и требовалось проверить. Результаты заносим в правый столбец. Таким образом, итоговая комбинационная таблица выглядит следующим образом:

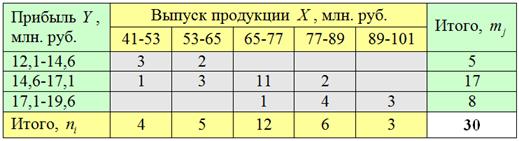
Сделаем выводы. На основании чего? Смотрим, как располагаются частоты (числа в серой области).

Если частоты имеют тенденцию располагаться по диагонали от левого верхнего до правого нижнего угла, то между признаками существует прямая корреляционная зависимость («чем больше, тем больше»). Это наш случай – по таблице хорошо видно, что с увеличением выпуска продукции растут и прибыли предприятий.

Если частоты имеют тенденцию располагаться по диагонали от левого нижнего до правого верхнего угла, то между признаками существует обратная корреляционная зависимость («чем больше, тем меньше»).

И, наконец, если частоты расположены хаотично, без явной закономерности, то корреляционная зависимость отсутствует либо является слабой.

Задание выполнено.

И здесь опять возникает вопрос: насколько СИЛЬНО влияет признак-фактор на признак-результат? Ответ на этот вопрос дают эмпирические показатели, о которых мы поговорим на следующем уроке, ну а пока аналогичное задание для самостоятельного решения:

Пример 64

Известны выборочные данные по 50 предприятиям одной отрасли – дебиторская задолженность (млн. руб.) и соответствующие дивиденды, начисленные по результатам деятельности (млн. руб.).

Справка: дебиторская задолженность – это то, что предприятию должны юридические и физические лица.

Определить признак-фактор и признак-результат и высказать предположение о наличии и направлении корреляционной зависимости. Проверить выдвинутое предположение, выполнив комбинационную группировку, при этом значения признака-фактора следует разделить на 6 равных интервалов, а значения признака результата – на 5 групп с одинаковым количеством предприятий в каждой. Сделать выводы.

…Как проверить предположение? Пока что визуально. Строим комбинационную таблицу и смотрим, по диагонали ли располагаются частоты, и если да, то по какой. Все расклады приведены в конце предыдущего примера.

Решаем прямо в MS Excel! И не ленимся – это задачи из реальных контрольных работ! Образец для сверки совсем близко, после чего переходим к рассмотрению эмпирических показателей, где речь зайдёт как раз о силе корреляционной зависимости.

Решения и ответы:

Пример 64. Решение: чем выше дебиторская задолженность предприятия, тем меньше у него свободных средств, которые могут быть направлены на выплату дивидендов, и, соответственно, тем меньше они могут быть. Таким образом, – дебиторская задолженность – признак-фактор, а  – начисленные дивиденды – признак-результат. Предполагаемая корреляционная зависимость  от – обратная (чем больше задолженность, тем в среднем могут быть меньше дивиденды).

Проверим выдвинутое предположение, построив комбинационную группировку. Упорядочим предприятия по возрастанию признака-фактора (дебиторской задолженности):

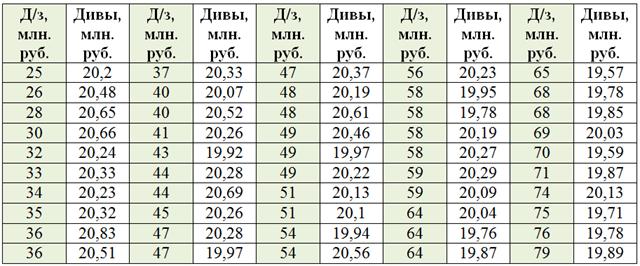
Вычислим размах вариации:  млн. руб. По условию, значения признака-фактора нужно разбить на  интервалов равной длины, таким образом, длина каждого интервала составит  млн. руб. В результате получаем следующие группы:

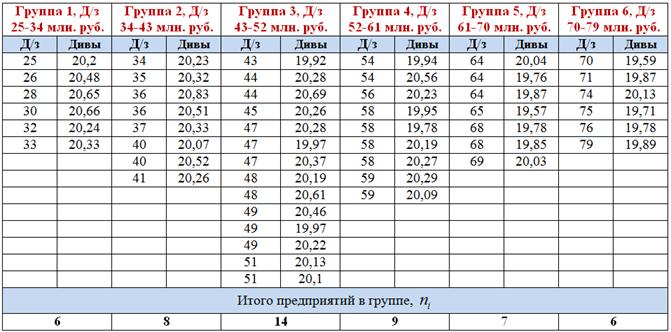
Контроль:

Проведём независимую сортировку дивидендов по возрастанию:

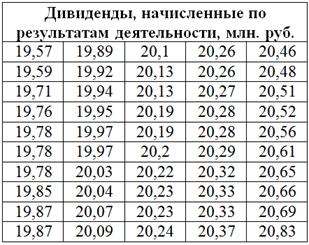
По условию, значения признака-результата следуют разбить на 5 групп с равным количеством предприятий в каждой, что и сделано в вышеприведённой таблице – в каждой группе у нас по  предприятий. В результате получаем 5 интервалов разной длины, при этом внутренние границы интервалов находим как среднее арифметическое «стыковых» значений:

В групповой таблице (см. ниже) ВНИМАТЕЛЬНО отмечаем:

– красным цветом – предприятия с дивидендами 19,57 - 19,88 млн. руб.;
– синим цветом – предприятия с дивидендами 19,88 - 20,095 млн. руб.;
– зелёным цветом – предприятия с дивидендами 20,095 - 20,25 млн. руб.;
– фиолетовым цветом – предприятия с дивидендами 20,25 - 20,415 млн. руб.;
– и оранжевым цветом – предприятия с дивидендами 20,415 - 20,83 млн. руб.

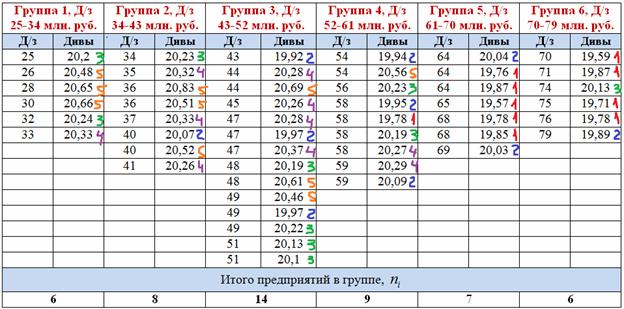
По каждой из 6 групп подсчитываем количество красных, синих, зелёных, фиолетовых и оранжевых предприятий, результаты заносим в комбинационную таблицу:

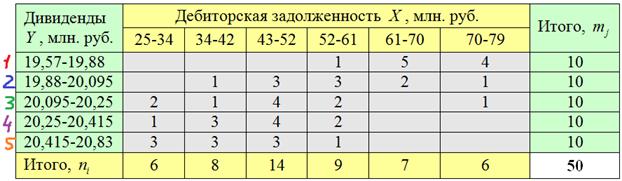
И обязательно проверка: по каждому серому столбцу подсчитываем суммы и убеждаемся, что получаются корректные значения  (нижняя строка). По каждой серой строке тоже подсчитываем суммы, получая равные значения  (правый столбец). Если где-то что-то «не сходится», значит, допущена ошибка по невнимательности.

Частоты имеют тенденцию располагаться по диагонали от левого нижнего к правому верхнему углу, что говорит о наличии обратной корреляционной зависимости  – начисленных дивидендов от  – дебиторской задолженности (чем больше задолженность, тем в среднем меньше дивиденды).

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте