


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Как привести квадратичную форму к каноническому виду?
Метод Лагранжа
Приветствую вас на втором уроке о квадратичных формах, который посвящен её каноническому виду и соответствующим методам. «Чайникам» и вновь прибывшим с поисковика рекомендую сначала ознакомиться первой частью – чтобы быстренько привести себя в форму :)
И мы сразу же продолжаем. Если в квадратичной форме отсутствуют слагаемые с парными произведениями переменных, то говорят, что она находится в каноническом виде. …Первая часть предложения была понятной? Тогда едем дальше.
Любую квадратичную форму можно привести к каноническому виду:
– форму двух переменных ![]() – к виду
– к виду ![]() (различаем коэффициенты «а» и «альфа»!);
(различаем коэффициенты «а» и «альфа»!);
– трёх переменных ![]() – к виду
– к виду ![]() ;
;
…
– форму ![]() переменных
переменных ![]() «простыня» – к виду:
«простыня» – к виду:
![]()
Чуть позже я сформулирую это утверждение более строго, расскажу о геометрическом смысле, да и просто смысле приведения – после того, как мы освоим техническую сторону вопроса.
И ключевой момент этой технической стороны состоит в линейных заменах:
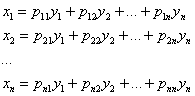 – ТАКИХ, которые как раз и приводят форму к каноническому виду.
– ТАКИХ, которые как раз и приводят форму к каноническому виду.
Систему часто записывают в виде компактного матричного уравнения ![]() , где:
, где:
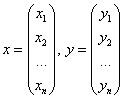 – столбцы старых и новых переменных,
– столбцы старых и новых переменных,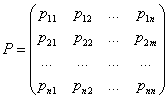 – матрица линейного преобразования.
– матрица линейного преобразования.
Внимание! Если вам не понятно, как из уравнения получить систему замен, обязательно посмотрите здесь (после Примера 3). Это важно.
Существует несколько способов приведения формы к каноническому виду, и в рамках сайта я расскажу о методе Лагранжа и методе ортогональных преобразований (уже следующий урок).
Начнём с наиболее простого метода:
Пример 6
Привести квадратичную форму к каноническому виду методом Лагранжа. Записать матрицу соответствующего линейного преобразования.
![]()
простенько и со вкусом
Решение: здесь используются стандартные замены ![]() с последующим применением бородатой формулы
с последующим применением бородатой формулы ![]() :
:
![]() – форма
– форма ![]() в каноническом виде.
в каноническом виде.
Запишем матрицу проведённого линейного преобразования: ![]() – она состоит из «игрековых» коэффициентов замен
– она состоит из «игрековых» коэффициентов замен ![]() .
.
Ответ: ![]() ,
, ![]()
Пример, конечно, прозрачный, но сразу зададимся вопросом – как выполнить проверку? Её можно выполнить матричным методом по формуле ![]() , где
, где ![]() – транспонированная матрица линейного преобразования,
– транспонированная матрица линейного преобразования, ![]() – исходная и
– исходная и ![]() – новая матрица квадратичной формы.
– новая матрица квадратичной формы.
В нашем случае ![]() – исходная матрица формы
– исходная матрица формы ![]() , и, перемножая три матрицы:
, и, перемножая три матрицы:
![]()
![]() – получаем матрицу формы
– получаем матрицу формы ![]() , что и требовалось проверить.
, что и требовалось проверить.
Но то был лишь частный случай:
Пример 7
Привести квадратичную форму к каноническому виду методом Лагранжа.
![]()
Записать матрицу соответствующего линейного преобразования.
Решение: когда в форме присутствуют квадраты переменных (а они есть почти всегда), то используется другой приём. Идея состоит в выделении полных квадратов по формулам ![]() ,
, ![]() с дальнейшей заменой переменных.
с дальнейшей заменой переменных.
Сначала выбираем какую-нибудь переменную, которая находится в квадрате, здесь можно выбрать ![]() или
или ![]() . Переменные традиционно перебирают по порядку, поэтому рассматриваем
. Переменные традиционно перебирают по порядку, поэтому рассматриваем ![]() и собираем вместе все слагаемые, где есть эта переменная:
и собираем вместе все слагаемые, где есть эта переменная:
![]()
«двойку» удобно вынести за скобки:
![]()
очевидно, всё дело сведётся к формуле ![]() , и нам нужно искусственно организовать данную конструкцию. Для этого в скобках прибавляем
, и нам нужно искусственно организовать данную конструкцию. Для этого в скобках прибавляем ![]() и, чтобы ничего не изменилось – за скобками проводим вычитание:
и, чтобы ничего не изменилось – за скобками проводим вычитание:
![]()
выделяем полный квадрат:
![]() , после чего выполним проверку обратными действиями – раскроем скобки и приведём подобные слагаемые:
, после чего выполним проверку обратными действиями – раскроем скобки и приведём подобные слагаемые:
![]() , ОК
, ОК
Теперь проведём замены ![]() :
:
![]() – форма
– форма ![]() в каноническом виде.
в каноническом виде.
И тут вроде бы можно записать матрицу линейного преобразования, но есть одна загвоздка, проведённые замены имеют вид ![]() :
:
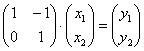
но нам-то нужна другая матрица – матрица ![]() уравнения
уравнения ![]() .
.
Для разрешения уравнения ![]() относительно
относительно ![]() умножим обе его части на
умножим обе его части на ![]() слева:
слева:
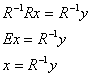
Я не буду подробно расписывать процесс нахождения обратной матрицы, а сразу приведу готовый результат ![]() – искомая матрица линейного преобразования. Напоминаю (см. начало урока), что в этой матрице находятся «игрековые» коэффициенты «прямых» замен:
– искомая матрица линейного преобразования. Напоминаю (см. начало урока), что в этой матрице находятся «игрековые» коэффициенты «прямых» замен:
![]()
Справка: возможно, ещё не все до конца понимают, как из матричного уравнения получается система замен. В правой части уравнения 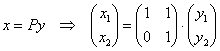 выполняем матричное умножение:
выполняем матричное умножение:
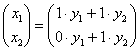
Две матрицы равны, если равны их соответствующие элементы, таким образом:
![]()
И в самом деле, выполняя прямые замены в форме ![]() :
:
![]()
![]() – получаем её канонический вид, найденный выше.
– получаем её канонический вид, найденный выше.
То же самое можно установить матричным методом. Запишем матрицу ![]() формы
формы ![]() и в результате перемножения трёх матриц:
и в результате перемножения трёх матриц:
![]()
![]() – получим «каноническую» матрицу.
– получим «каноническую» матрицу.
Прямая подстановка, безусловно, удобнее, но особенность метода Лагранжа состоит в том, что к канонической форме мы подбираемся «с другой стороны» (за исключением немногочисленных случаев наподобие предыдущего примера).
Ответ: ![]() ,
, ![]()
Если условие не запрашивает линейное преобразование, то решение заметно сократится. Но мы его наоборот – ещё больше увеличим :) В образовательных целях.
Квадратичную форму можно привести к каноническому виду не единственным способом. Это следует уже из самого алгоритма действий. Так, например, полный квадрат можно выделить без выноса «двойки» за скобку:
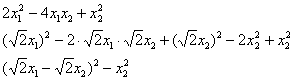
контроль: ![]()
и, после замен 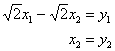 тоже получается канонический, но уже другой вид рассматриваемой формы:
тоже получается канонический, но уже другой вид рассматриваемой формы:
![]()
Кстати, начать можно и со 2-й переменной –
выполните это задание самостоятельно:
Привести квадратичную форму ![]() к каноническому виду, выделив полный квадрат при переменной
к каноническому виду, выделив полный квадрат при переменной ![]() . Записать матрицу соответствующего линейного преобразования.
. Записать матрицу соответствующего линейного преобразования.
Решение и ответ в конце урока.
Повысим уровень сложности, а точнее, количество переменных:
Пример 8
Привести квадратичную форму к каноническому виду методом Лагранжа
![]()
Записать матрицу соответствующего линейного преобразования.
Решать начинаем традиционно – группируем все слагаемые, которые содержат 1-ю переменную:
![]()
и начинаем конструировать полный квадрат:
![]()
здесь чётко просматривается формула ![]() и для её применения мы должны прибавить и вычесть
и для её применения мы должны прибавить и вычесть ![]() :
:
![]()
«собираем» квадрат суммы и упрощаем «хвост», распишу это упрощение подробно:
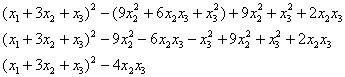
контроль: ![]()
![]() – ч.т.п.
– ч.т.п.
На следующем шаге обычно выделяется ещё один полный квадрат, но у нас осталось единственно слагаемое с парным произведением, и в подобной ситуации сразу же выполняются замены, в данном случае ![]() :
:
![]()
В результате получен неканонический вид формы и поэтому нам потребуется ещё одна замена. Используем стандартный трюк, который встретился в самом начале урока:
![]() . Таким образом, получаем:
. Таким образом, получаем:
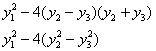
![]() – форма
– форма ![]() в каноническом виде.
в каноническом виде.
Теперь нужно записать матрицу соответствующего линейного преобразования. Ситуация осложнятся тем, что мы провели ДВА преобразования, и нам предстоит найти их композицию – результирующее преобразование, которое выражает ![]() через сумму / разность «игреков».
через сумму / разность «игреков».
Давайте разбираться, что к чему. Запишем первую замену 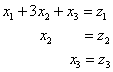 в матричной форме:
в матричной форме: 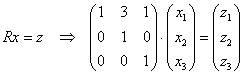 .
.
Вторая же замена 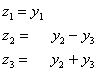 имеет несколько другой вид:
имеет несколько другой вид:
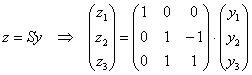
Из уравнений ![]() следует, что:
следует, что:
![]()
Для разрешения полученного уравнения относительно ![]() умножим обе его части на
умножим обе его части на ![]() слева:
слева:
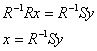
Таким образом, нам нужно найти обратную матрицу 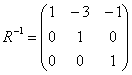 (уже не нужно:)) и выполнить матричное умножение:
(уже не нужно:)) и выполнить матричное умножение:
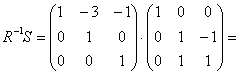
 – получив тем самым искомое результирующее преобразование.
– получив тем самым искомое результирующее преобразование.
Но подставлять 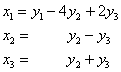 в форму
в форму ![]() что-то неохота, и поэтому «пропустим через мясорубку» её матрицу
что-то неохота, и поэтому «пропустим через мясорубку» её матрицу 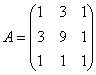 , благо, матричный калькулятор под рукой:
, благо, матричный калькулятор под рукой:
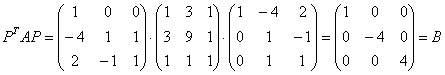 – получена матрица приведённой формы
– получена матрица приведённой формы ![]() , в чём мы и хотели убедиться.
, в чём мы и хотели убедиться.
Обратите внимание на удобство матричной записи и матричного метода – они практически «сводят на нет» путаницу в индексах и степенях квадратичной формы.
Ответ: ![]() ,
, 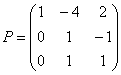
Тренируемся:
Пример 9
Привести квадратичную форму к каноническому виду методом Лагранжа
а) ![]()
б) ![]() – особенно часто встречающийся тип приведения.
– особенно часто встречающийся тип приведения.
В образцах решения использован «традиционный» путь, т.е. полные квадраты выделяются по порядку, начиная с 1-й переменной. Перед заменой переменных полезно выполнять обратный ход – раскрывать скобки и приводить подобные слагаемые, чтобы получить исходный вид. Это вполне надёжный способ проверки. Также обратите внимание, что здесь не требуется указывать линейное преобразование, однако, я коротко рассказал, как его находить (мало ли, понадобится).
…У всех всё получилось? Тогда продолжаем – начинается самое интересное! Наверное, все понимают, что подавляющее большинство линейных преобразований не приводят нас к желаемому результату. Вернёмся к подопытной форме ![]() Примера 7 и проведём, например, такую замену:
Примера 7 и проведём, например, такую замену: ![]() .
.
Запишем матрицу формы ![]() , матрицу преобразования
, матрицу преобразования ![]() и воспользуемся знакомой формулой:
и воспользуемся знакомой формулой:
![]()
![]()
Таким образом, форма ![]() приняла другой, тоже неканонический вид
приняла другой, тоже неканонический вид ![]() .
.
И тут я хочу отметить ещё одно преимущество матричного решения, о котором не говорил. В результате умножения ![]() ДОЛЖНА получиться симметрическая и только такая матрица, и этот факт значительно снижает риск пропустить ошибку. Но, разумеется, можно выполнить и прямую подстановку
ДОЛЖНА получиться симметрическая и только такая матрица, и этот факт значительно снижает риск пропустить ошибку. Но, разумеется, можно выполнить и прямую подстановку ![]() в
в ![]() :
:
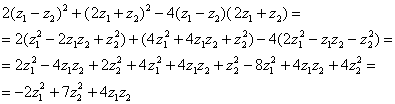
Правда, запутаться тут легче и гарантий никаких.
Далее. Все преобразования, которые нам встретились выше, не вырождены. Что это означает? Это означает, что для них существует обратное преобразование – образно говоря, «путь назад». Теперь не образно:) определитель матрицы невырожденного линейного преобразования непременно отличен от нуля ![]() , что гарантирует существование обратной матрицы
, что гарантирует существование обратной матрицы ![]() и «зеркальной» формулы
и «зеркальной» формулы ![]() , с помощью которой мы можем однозначно восстановить исходную матрицу
, с помощью которой мы можем однозначно восстановить исходную матрицу ![]() .
.
Чего не скажешь о преобразовании вырожденном – это «билет в один конец». Одним из таких преобразований является тривиальное нулевое преобразование. Так, например, если ![]() , то форма
, то форма ![]() вырождается в нулевую форму
вырождается в нулевую форму ![]() с матрицей
с матрицей ![]() . Обратного пути нет, то есть, если нам изначально дана вырожденная «игрековая» форма с матрицей
. Обратного пути нет, то есть, если нам изначально дана вырожденная «игрековая» форма с матрицей ![]() , то невозможно выяснить, от какой формы она произошла.
, то невозможно выяснить, от какой формы она произошла.
Существуют и другие типы «вырождения», но всех их объединяет тот факт, что определитель матрицы такого преобразования равен нулю: ![]() , из чего следует, что обратной матрицы не существует, а значит, не существует и возврата.
, из чего следует, что обратной матрицы не существует, а значит, не существует и возврата.
А теперь заметим, что нулевое преобразование привело нас… к каноническому виду ![]() ! И в самом деле – это же канонический вид по определению. И поэтому сейчас мы усилим утверждение, сформулированное в начале урока: любую квадратичную форму можно привести к каноническому виду с помощью невырожденного линейного преобразования. Существование такого преобразования, в частности, гарантирует метод Лагранжа.
! И в самом деле – это же канонический вид по определению. И поэтому сейчас мы усилим утверждение, сформулированное в начале урока: любую квадратичную форму можно привести к каноническому виду с помощью невырожденного линейного преобразования. Существование такого преобразования, в частности, гарантирует метод Лагранжа.
И сейчас я озвучу кульминационный и ОЧЕНЬ важный момент: невырожденное линейное преобразование не меняет СУЩНОСТИ квадратичной формы. Здесь можно привести такой ассоциативный пример: рассмотрим произвольную ненулевую форму ![]() и представим, что это квадратный лист бумаги, на котором записано некое слово. Если форма находится в неканоническом виде, то лист занимает такое положение, в котором мы слова не видим, или же только догадываемся, что это за слово.
и представим, что это квадратный лист бумаги, на котором записано некое слово. Если форма находится в неканоническом виде, то лист занимает такое положение, в котором мы слова не видим, или же только догадываемся, что это за слово.
1) Невырожденное преобразование, которое приводит форму к каноническому виду, поворачивает листок бумаги к нам «лицом» – чтобы слово было отчётливо видно. Поскольку таких преобразований на самом деле много, то лист бумаги в общем случае будет менять свой размер и местоположение, и размер шрифта тоже будет меняться. Но что не изменится – так это слово.
2) Невырожденное преобразование, которое НЕ приводит форму к каноническому виду, делает то же самое с большим и толстым нюансом: слова мы по-прежнему не видим.
3) Вырожденное линейное преобразование либо полностью стирает с листа слово (нулевое преобразование), либо стирает отдельные буквы – так, чтобы нельзя было однозначно сказать, от какого слова они остались; причём, мы можем не увидеть даже и этих букв (если форма осталась в неканоническом виде).
И, завершая ассоциацию, отметим наиболее интересный случай – когда невырожденное преобразование не только приводит форму к каноническому виду, но ещё и сохраняет размер листа, т.е. поворачивает его к нам в неизменном виде. Жду вас на третьем уроке о методе ортогонального преобразования, где мы продолжим увлекательную беседу и вложим в сущность формы конкретный геометрический смысл.
Решения и ответы:
Задание к Примеру 7. Решение: приведём форму ![]() к каноническому виду
к каноническому виду
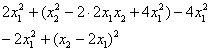
Проведём замены ![]() :
:
![]() – форма
– форма ![]() в каноническом виде.
в каноническом виде.
Найдём матрицу линейного преобразования ![]() , где
, где ![]() – матрица «иксовых» коэффициентов проведённых замен.
– матрица «иксовых» коэффициентов проведённых замен.
В данном случае ![]() (см. урок Как найти обратную матрицу?)
(см. урок Как найти обратную матрицу?)
Выполним проверку прямой подстановкой ![]() в
в ![]() :
:
![]() , что и требовалось проверить.
, что и требовалось проверить.
Ответ: ![]() ,
, ![]()
Пример 9. Решение:
а) проведём замены ![]() :
:
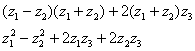
Полученная форма имеет неканонический вид, и здесь следует выделить полные квадраты. Начнём с переменной ![]() :
:
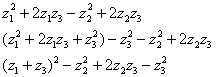
теперь выделяем квадрат при переменной ![]() :
:
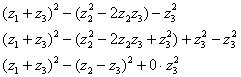
Контроль: ![]()
![]() , что и требовалось проверить.
, что и требовалось проверить.
Проведём замены: ![]()
Ответ: ![]()
Примечание: проведённые замены можно записать в виде матричных уравнений ![]() . Из последнего уравнения выразим
. Из последнего уравнения выразим ![]() и подставим в первое уравнение:
и подставим в первое уравнение: ![]() . Таким образом, для нахождения матрицы итогового линейного преобразования нужно найти
. Таким образом, для нахождения матрицы итогового линейного преобразования нужно найти ![]() и выполнить умножение
и выполнить умножение ![]() .
.
б) Решение: выделим полный квадрат при 1-й переменной:
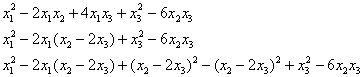
«собираем» полный квадрат и упрощаем «хвост»:
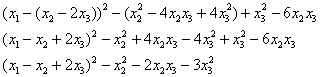
выделим полный квадрат при 2-й переменной:
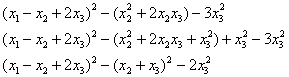
Выполним проверку раскрыв все скобки:
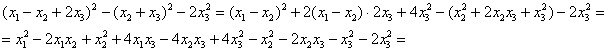
![]() – получен исходный вид формы.
– получен исходный вид формы.
Проведём замены: ![]()
Ответ: ![]()
Примечание: выполненные замены имеют вид ![]() , таким образом, матрица линейного преобразования:
, таким образом, матрица линейного преобразования:![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright