Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Графики и основные свойства элементарных функций

Данный методический материал носит справочный характер и относится к широкому кругу тем. В статье приведен обзор графиков основных элементарных функций и рассмотрен важнейший вопрос – как правильно и БЫСТРО построить график. В ходе изучения высшей математики без знания графиков основных элементарных функций придётся тяжело, поэтому очень важно вспомнить, как выглядят графики параболы, гиперболы, синуса, косинуса и т.д., запомнить некоторые значения функций. Также речь пойдет о некоторых свойствах основных функций.

Я не претендую на полноту и научную основательность материалов, упор будет сделан, прежде всего, на практике – тех вещах, с которыми приходится сталкиваться буквально на каждом шагу, в любой теме высшей математики. Графики для чайников? Можно сказать и так.

По многочисленным просьбам читателей кликабельное оглавление:

• Как правильно построить координатные оси?
• График линейной функции (прямая)
• График квадратичной функции (парабола)
• График кубической функции (кубическая парабола)
• Графики функций-многочленов более высоких степеней
• График функции 
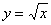
• График гиперболы
• График показательной функции на примере
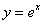
• График логарифмической функции на примере
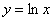
• Графики тригонометрических функций:
• синуса;
• косинуса;
• тангенса и котангенса.
• Графики обратных тригонометрических функций:
• арксинуса;
• арккосинуса;
• арктангенса и арккотангенса;


• Элементарные преобразования графиков (сдвиги, растяжения и т.д.)

Кроме того, есть сверхкраткий конспект по теме
– освойте 16 видов графиков, изучив ШЕСТЬ страниц!

Серьёзно, шесть, удивился даже я сам. Данный конспект содержит улучшенную графику и доступен за символическую плaту, демо-версию можно посмотреть здесь. Файл удобно распечатать, чтобы графики всегда были под рукой. Спасибо за поддержку проекта!

И сразу начинаем:

Как правильно построить координатные оси?

На практике контрольные работы почти всегда оформляются студентами в отдельных тетрадях, разлинованных в клетку. Зачем нужна клетчатая разметка? Ведь работу, в принципе, можно сделать и на листах А4. А клетка необходима как раз для качественного и точного оформления чертежей.

Любой чертеж графика функции начинается с координатных осей.

Чертежи бывают двухмерными и трехмерными.

Сначала рассмотрим двухмерный случай декартовой прямоугольной системы координат:

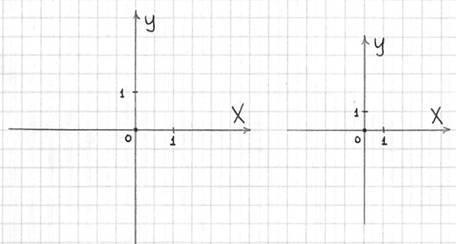
1) Чертим координатные оси. Ось называется осью абсцисс, а ось – осью ординат. Чертить их всегда стараемся аккуратно и не криво. Стрелочки тоже не должны напоминать бороду Папы Карло.

2) Подписываем оси большими буквами «икс» и «игрек». Не забываем подписывать оси.

3) Задаем масштаб по осям: рисуем ноль и две единички. При выполнении чертежа самый удобный и часто встречающийся масштаб: 1 единица = 2 клеточки (чертеж слева) – по возможности придерживайтесь именно его. Однако время от времени случается так, что чертеж не вмещается на тетрадный лист – тогда масштаб уменьшаем: 1 единица = 1 клеточка (чертеж справа). Редко, но бывает, что масштаб чертежа приходится уменьшать (или увеличивать) еще больше

НЕ НУЖНО «строчить из пулемёта» …-5, -4, -3, -1, 0, 1, 2, 3, 4, 5, …. Ибо координатная плоскость – не памятник Декарту, а студент – не голубь. Ставим ноль и две единицы по осям. Иногда вместо единиц удобно «засечь» другие значения, например, «двойку» на оси абсцисс и «тройку» на оси ординат – и эта система (0, 2 и 3) тоже однозначно задаст координатную сетку.

Предполагаемые размеры чертежа лучше оценить ещё ДО построения чертежа. Так, например, если в задании требуется начертить треугольник с вершинами ,  , , то совершенно понятно, что популярный масштаб 1 единица = 2 клеточки не подойдет. Почему? Посмотрим на точку  – здесь придется отмерять пятнадцать сантиметров вниз, и, очевидно, что чертеж  не вместится (или вместится еле-еле) на тетрадный лист. Поэтому сразу выбираем более мелкий масштаб 1 единица = 1 клеточка.

Кстати, о сантиметрах и тетрадных клетках. Правда ли, что в 30 тетрадных клетках содержится 15 сантиметров? Отмерьте в тетради для интереса 15 сантиметров линейкой. В СССР, возможно, это было правдой… Интересно отметить, что если отмерить эти самые сантиметры по горизонтали  и вертикали, то результаты (в клетках) будут разными! Строго говоря, современные тетради не клетчатые, а прямоугольные. Возможно, это покажется ерундой, но, чертить, например, окружность циркулем при таких раскладах очень неудобно. Если честно, в такие моменты начинаешь задумываться о правоте товарища Сталина, который отправлял в лагеря за халтуру на производстве, не говоря уже об отечественном автомобилестроении, падающих самолетах или взрывающихся электростанциях.

К слову о качестве, или краткая рекомендация по канцтоварам. На сегодняшний день большинство тетрадей в продаже, плохих слов не говоря, полное гомно. По той причине, что они промокают, причём не только от гелевых, но и от шариковых ручек! На бумаге экономят. Для оформления контрольных работ рекомендую использовать тетради Архангельского ЦБК (18 листов, клетка) или «Пятёрочку», правда, она дороже. Ручку желательно выбрать гелевую, даже самый дешевый китайский гелевый стержень намного лучше, чем шариковая ручка, которая то мажет, то дерёт бумагу. Единственной «конкурентоспособной» шариковой ручкой на моей памяти является «Эрих Краузе». Она пишет чётко, красиво и стабильно – что с полным стержнем, что с практически пустым.

Дополнительно: вИдение прямоугольной системы координат глазами аналитической геометрии освещается в статье Линейная (не) зависимость векторов. Базис векторов, подробную информацию о координатных четвертях можно найти во втором параграфе урока Линейные неравенства.

Трехмерный случай

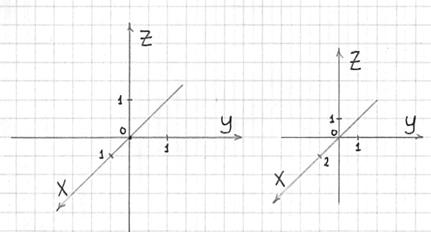
Здесь почти всё так же.

1) Чертим координатные оси. Стандарт: ось аппликат  – направлена вверх, ось  – направлена вправо, ось  – влево вниз  строго под углом 45 градусов.

2) Подписываем оси.

3) Задаем масштаб по осям. Масштаб по оси  – меньше, чем масштаб по другим осям. Также обратите внимание, что на правом чертеже я использовал нестандартную «засечку» по оси  (о такой возможности уже упомянуто выше). С моей точки зрения, так точнее, быстрее и эстетичнее – не нужно под микроскопом выискивать середину клетки и «лепить» единицу впритык к началу координат.

При выполнении трехмерного чертежа опять же – отдавайте приоритет масштабу
1 единица = 2 клетки по осям и (чертеж слева) и 1 единица = диагональ одной клетки  – по оси .

...Для чего нужны все эти правила? Правила существуют для того, чтобы их нарушать. Чем я сейчас и займусь. Дело в том, что последующие чертежи статьи будут выполнены мной в Экселе, и, координатные оси будут выглядеть некорректно с точки зрения правильного оформления. Я бы мог начертить все графики от руки, но чертить их на самом деле жуть как неохота Эксель их начертит гораздо точнее.

Графики и основные свойства элементарных функций

График линейной функции

Линейная функция задается уравнением . График линейной функций представляет собой прямую. Для того, чтобы построить прямую достаточно знать две точки.

Пример 1

Построить график функции . Найдем две точки. В качестве одной из точек выгодно выбрать ноль.

Если , то

Берем еще какую-нибудь точку, например, 1.

Если , то

При оформлении заданий координаты точек обычно сводятся в таблицу:

 
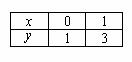
А сами значения рассчитываются устно или на черновике, калькуляторе.

Две точки найдены, выполним чертеж:

При оформлении чертежа всегда подписываем графики.

Не лишним будет вспомнить частные случаи линейной функции:

Обратите внимание, как я расположил подписи, подписи не должны допускать разночтений при изучении чертежа. В данном случае крайне нежелательно было поставить подпись рядом с точкой пересечения прямых  ,  или справа внизу между графиками.

1) Линейная функция вида  () называется прямой пропорциональностью. Например, . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.

2) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции строится сразу, без нахождения всяких точек. То есть, запись  следует понимать так: «игрек всегда равен –4, при любом значении икс».

3) Уравнение вида  задает прямую, параллельную оси , в частности, сама ось  задается уравнением . График функции также строится сразу. Запись  следует понимать так: «икс всегда, при любом значении игрек, равен 1».

Некоторые спросят, ну зачем вспоминать 6 класс?! Так-то оно, может и так, только за годы практики я встретил добрый десяток студентов, которых ставила в тупик задача построения графика вроде  или .

Построение прямой – самое распространенное действие при выполнении чертежей.

Прямая линия детально рассматривается в курсе аналитической геометрии, и желающие могут обратиться к статье Уравнение прямой на плоскости.

График квадратичной, кубической функции, график многочлена

Парабола. График квадратичной функции  () представляет собой параболу. Рассмотрим знаменитый случай:

Вспоминаем некоторые свойства функции .

Область определения – любое действительное число (любое значение «икс»). Что это значит? Какую бы точку на оси  мы не выбрали – для каждого «икс» существует точка параболы. Математически это записывается так: . Область определения любой функции стандартно обозначается через  или . Буква  обозначает множество действительных чисел или, проще говоря, «любое икс»  (когда работа оформляется в тетради, пишут не фигурную букву , а жирную букву R).    

Область значений – это множество всех значений, которые может принимать переменная «игрек». В данном случае:  – множество всех положительных значений, включая ноль. Область значений стандартно обозначается через  или .

Функция  является чётной. Если функция является чётной, то ее график симметричен относительно оси . Это очень полезное свойство, которое заметно упрощает построение графика, в чём мы скоро убедимся. Аналитически чётность функции выражается условием . Как проверить любую функцию на чётность? Нужно  вместо  подставить в уравнение . В случае с параболой проверка выглядит так: , значит, функция  является четной.

Функция  не ограничена сверху. Аналитически свойство записывается так: . Вот вам, кстати, и пример геометрического смысла предела функции: если мы будем уходить по оси  (влево или вправо) на бесконечность, то ветки параболы (значения «игрек») будут неограниченно уходить вверх  на «плюс бесконечность».

При изучении пределов функций желательно понимать геометрический смысл предела.

Я не случайно так подробно расписал свойства функции, все вышеперечисленные вещи полезно знать и помнить при построении графиков функций, а также при исследовании графиков функций.

Пример 2

Построить график функции .

В этом примере мы рассмотрим важный технический вопрос: Как быстро построить параболу? В практических заданиях необходимость начертить параболу возникает очень часто, в частности, при вычислении площади фигуры с помощью определенного интеграла. Поэтому чертеж желательно научиться выполнять быстро, с минимальной потерей времени. Я предлагаю следующий алгоритм построения.

Сначала находим вершину параболы. Для этого берём первую производную и приравниваем ее к нулю:

Если с производными плохо, следует ознакомиться с уроком Как найти производную?

Итак, решение нашего уравнения:  – именно в этой точке и находится вершина параболы. Почему это так, можно узнать из теоретической статьи о производной и урока об экстремумах функции. А пока рассчитываем соответствующее значение «игрек»:

Таким образом, вершина находится в точке

Теперь находим другие точки, при этом нагло пользуемся симметричностью параболы. Следует заметить, что функция  – не является чётной, но, тем не менее, симметричность параболы никто не отменял.

В каком порядке  находить остальные точки, думаю, будет понятно из итоговой таблицы:

Данный алгоритм построения образно можно назвать «челноком» или  принципом «туда-сюда» с Анфисой Чеховой.

Выполним чертеж:

Из рассмотренных графиков вспоминается еще один полезный признак:

Для квадратичной функции  () справедливо следующее:

Если , то ветви параболы направлены вверх.

Если , то ветви параболы направлены вниз.

Углублённые знания о кривой можно получить на уроке Гипербола и парабола.

Кубическая парабола

Кубическая парабола задается функцией . Вот знакомый со школы чертеж:

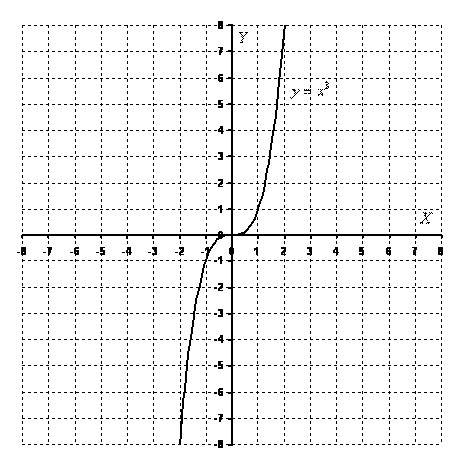
Перечислим основные свойства функции

Область определения – любое действительное число:.

Область значений – любое действительное число:.

Функция  является нечётной. Если функция является нечётной, то ее график симметричен относительно начала координат. Аналитически нечётность функции выражается условием . Выполним проверку для кубической функции, для этого вместо «икс» подставим «минус икс»:
, значит, функция  является нечетной.

Функция  не ограничена. На языке пределов функции это можно записать так: ,

Кубическую параболу тоже удобнее строить с помощью алгоритма «челнока»:

Наверняка, вы заметили, в чем ещё проявляется нечетность функции. Если мы нашли, что , то при вычислении  уже не нужно ничего считать, автоматом записываем, что . Эта особенность справедлива для любой нечетной функции.

А теперь поговорим о графиках функций-многочленов высоких степеней чуть более подробно. График функции  () принципиально имеет следующий вид:

В этом примере коэффициент при старшей степени , поэтому график развёрнут «наоборот». Принципиально такой же вид имеют графики функций-многочленов 5-й, 7-й, 9-й и других нечетных степеней. Чем выше степень, тем больше промежуточных «загибулин».

Функции-многочлены 4-й, 6-й и других четных степеней имеют график принципиально следующего вида:

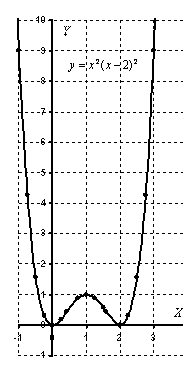
Эти знания полезны при исследовании графиков функций.

График функции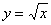

Он представляет собой одну из ветвей параболы. Выполним чертеж:

Основные свойства функции :

Область определения: .

Область значений: .

То есть, график функции полностью находится в первой координатной четверти.

Функция  не ограничена сверху. Или с помощью предела:

При построении простейших графиков с корнями также уместен поточечный способ построения, при этом выгодно подбирать такие значения «икс», чтобы корень извлекался нацело:

На самом деле хочется разобрать еще примеры с корнями, например, , но они встречаются значительно реже. Сейчас я ориентируюсь на более распространенные случаи, и, как показывает практика, что-нибудь вроде  приходиться строить значительно чаще. Однако унывать не нужно, в других статьях я рассмотрю самые разнообразные функции и их графики, корни в том числе.

График гиперболы

Опять же вспоминаем тривиальную «школьную» гиперболу .

Выполним чертеж:

Основные свойства функции :

Область определения: .

Область значений: .

Запись  обозначает: «любое действительное число, исключая ноль»

В точке  функция терпит бесконечный разрыв. Или с помощью односторонних пределов: , . Немного поговорим об односторонних пределах. Запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю слева. Как при этом ведёт себя график? Он уходит вниз на минус бесконечность, бесконечно близко приближаясь к оси . Именно этот факт и записывается пределом . Аналогично, запись  обозначает, что мы бесконечно близко приближаемся по оси  к нулю справа.  При этом ветвь гиперболы уходит вверх на плюс бесконечность, бесконечно близко приближаясь к оси . Или коротко: .

Такая прямая (к которой бесконечно близко приближается график какой-либо функции) называется асимптотой.

В данном случае ось  является вертикальной асимптотой для графика гиперболы при .

Будет ГРУБОЙ ошибкой, если при оформлении чертежа по небрежности допустить пересечение графика с асимптотой.

Также односторонние пределы ,  говорят нам о том, что гипербола не ограничена сверху и не ограничена снизу.

Исследуем функцию на бесконечности: , то есть, если мы начнем уходить  по оси  влево (или вправо) на бесконечность, то  «игреки» стройным  шагом будут бесконечно близко приближаться к нулю, и, соответственно, ветви гиперболы бесконечно близко приближаться к оси .

Таким образом, ось  является горизонтальной асимптотой для графика функции, если «икс» стремится к плюс или минус бесконечности.

Функция  является нечётной, а, значит, гипербола симметрична относительно начала координат. Данный факт очевиден из чертежа, кроме того, легко проверяется аналитически: .

График функции вида  () представляет собой две ветви гиперболы.

Если , то гипербола расположена в первой и третьей координатных четвертях (см. рисунок выше).

Если , то гипербола расположена во второй и четвертой координатных четвертях.

Указанную закономерность места жительства гиперболы нетрудно проанализировать с точки зрения геометрических преобразований графиков.

Пример 3

Построить правую ветвь гиперболы

Используем поточечный метод построения, при этом, значения  выгодно подбирать так, чтобы делилось нацело:

Выполним чертеж:

Не составит труда построить и левую ветвь гиперболы, здесь как раз поможет нечетность функции. Грубо говоря, в таблице поточечного построения мысленно добавляем к каждому числу минус, ставим соответствующие точки и прочерчиваем вторую ветвь.

Детальную геометрическую информацию о рассмотренной линии можно найти в статье Гипербола и парабола.

График показательной функции

В данном параграфе я сразу рассмотрю экспоненциальную функцию , поскольку в задачах высшей математики в 95% случаев встречается именно экспонента.

Напоминаю, что  – это иррациональное число: , это потребуется при построении графика, который, собственно, я без церемоний и построю. Трёх точек, пожалуй, хватит:

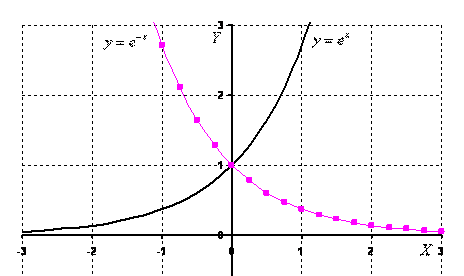
График функции  пока оставим в покое, о нём позже.

Основные свойства функции :

Область определения:  – любое «икс».

Область значений: . Обратите внимание, что ноль не включается в область значений. Экспонента – функция положительная, то есть для любого «икс» справедливо неравенство , а сам график экспоненты полностью расположен в верхней полуплоскости.

Функция не ограничена сверху: , то есть, если мы начнем уходить по оси  вправо на плюс бесконечность, то соответствующие значения «игрек» стройным шагом будут тоже уходить вверх на  по оси  . Кстати, график экспоненциальной функции будет «взмывать» вверх на бесконечность очень быстро и круто, уже при   

Исследуем поведение функции на минус бесконечности: . Таким образом, ось  является горизонтальной асимптотой для графика функции , если

Принципиально такой же вид имеет любая показательная функция , если . Функции , ,  будут отличаться только крутизной наклона графика, причем, чем больше основание, тем круче будет график.

Обратите внимание, что во всех случаях графики проходят через точку , то есть . Это значение должен знать даже «двоечник».

Теперь рассмотрим случай, когда основание . Снова пример с экспонентой  – на чертеже соответствующий график прочерчен малиновым цветом? Что произошло? Ничего особенного – та же самая экспонента, только она «развернулась в другую сторону». Об этой метаморфозе можно получить подробную информацию в статье Построение графиков с помощью геометрических преобразований.

Принципиально так же выглядят графики функций ,  и т. д.

Должен сказать, что второй случай встречается на практике реже, но он встречается, поэтому я счел нужным включить его в данную статью.

График логарифмической функции

Рассмотрим функцию с натуральным логарифмом .
Выполним поточечный чертеж:

Если позабылось, что такое логарифм, пожалуйста, обратитесь к школьным учебникам.

Основные свойства функции :

Область определения:

Область значений: .

Функция не ограничена сверху: , пусть и медленно, но ветка логарифма уходит вверх на бесконечность.
Исследуем поведение функции вблизи нуля справа: . Таким образом, ось  является вертикальной  асимптотой для графика функции при «икс» стремящемся к нулю справа.

Обязательно нужно знать и помнить типовое значение логарифма: .

Принципиально так же выглядит график логарифма при основании : , ,  (десятичный логарифм по основанию 10) и т.д. При этом, чем больше основание, тем более пологим будет график.

Случай  рассматривать не будем, что-то я не припомню, когда последний раз строил график с таким основанием. Да и логарифм вроде  в задачах высшей математики ооочень редкий гость.

В заключение параграфа скажу еще об одном факте: Экспоненциальная функция  и логарифмическая функция  – это две взаимно обратные функции. Если присмотреться к графику логарифма, то можно увидеть, что это – та же самая экспонента, просто она расположена немного по-другому.

Графики тригонометрических функций

С чего начинаются тригонометрические мучения в школе? Правильно. С синуса

Построим график функции

Данная линия называется синусоидой.

Напоминаю, что «пи» – это иррациональное число: , и в тригонометрии от него в глазах рябит.

Основные свойства функции :

Данная функция является периодической с периодом . Что это значит? Посмотрим на отрезок . Слева и справа от него бесконечно повторяется точно такой же кусок графика.

Область определения: , то есть для любого значения «икс» существует значение синуса.

Область значений: . Функция  является ограниченной: , то есть, все «игреки» сидят строго в отрезке .
Такого не бывает:  или , точнее говоря, бывает, но указанные уравнения не имеют решения.

Синус – это функция нечетная, синусоида симметричная относительно начала координат, и справедлив следующий факт: . Таким образом, если в вычислениях встретится, например, , то минус терять здесь ни в коем случае нельзя! Он выносится:

Как ведет себя синус на бесконечности? Попробуем провести исследование с помощью пределов:
,  Чему равны такие пределы? Запомните, данных пределов не существует. По вполне понятным причинам, график синуса болтается как как неприкаянный, то дойдет единицы, то уйдет к минус единице и так до бесконечности.

Вот вам пример, когда предела не существует. В высшей математике это можно встретить не очень часто, но такое понятие, как «предела не существует» – существует!

В практических вычислениях желательно (и даже обязательно) знать и помнить следующие значения синуса: , , . Другие значения синуса (а также остальных тригонометрических функций) можно найти в методическом материале Тригонометрические таблицы.

График косинуса

Построим график функции

График косинуса – это та же самая синусоида, сдвинутая вдоль оси  на  влево
(см. также Пример 8 урока о геометрических преобразованиях графиков).

Поэтому почти все свойства синуса справедливы и для косинуса. За некоторым, но существенным исключением.

Косинус – это функция четная, ее график симметричен относительно оси  , и справедлив следующий факт: . То есть, минус перед аргументом косинуса можно безболезненно убирать (или наоборот, ставить). В отличие от синуса в косинусе минус «бесследно пропадает».

Для решения практических задач нужно знать и помнить следующие значения косинуса: , , .

Графики тангенса и котангенса

Построим график функции

Основные свойства функции :

Данная функция является периодической с периодом . То есть, достаточно рассмотреть отрезок , слева и справа от него ситуация будет бесконечно повторяться.

Область определения:  – все действительные числа, кроме …  , , , … и т. д. или коротко: , где  – любое целое число. Множество целых чисел (… -4, -3, -2, -1, 0, 1, 2, 3, 4, …) в высшей математике обозначают жирной буквой Z.

Область значений: . Функция  не ограничена. В этом легко убедиться и аналитически:
 – если мы приближаемся по оси  к значению  справа, то ветка тангенса уходит на минус бесконечность, бесконечно близко приближаясь к своей асимптоте .
 – если мы приближаемся по оси  к значению  слева, то «игреки» шагают вверх на плюс бесконечность, а ветка тангенса бесконечно близко приближается к асимптоте .

Тангенс – функция нечетная, как и в случае с синусом, минус из-под тангенса не теряется, а выносится: .

В практических вычислениях полезно помнить следующие значения тангенса: , , , а также те точки, в которых тангенса не существует (см. график).

График котангенса – это почти тот же самый тангенс, функции связаны тригонометрическим соотношением . Вот его график:

Свойства попробуйте сформулировать самостоятельно, они практически такие же, как и у тангенса.

Графики обратных тригонометрических функций

Построим график арксинуса

Перечислим основные свойства функции :

Область определения: , не существует значений вроде  или

Область значений: , то есть,  функция  ограничена.

Арксинус – функция нечетная, здесь минус опять же выносится: .

В практических вычислениях полезно помнить следующие значения арксинуса: , , . Другие распространенные значения арксинуса (а также других «арков») можно найти с помощью таблицы значений обратных тригонометрических функций.

Построим график арккосинуса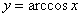

Очень похоже на арксинус, свойства функции сформулируйте самостоятельно. Остановлюсь на единственном моменте. В данной статье очень много разговоров шло о четности  и нечетности функций, и, возможно, у некоторых сложилось впечатление, что функция обязательно должна быть четной или нечетной. В общем случае, это, конечно, не так. Чаще всего, функция, которая вам встретится на практике – «никакая». В частности, арккосинус не является четной или нечетной функцией, он как раз «никакой».

Построим график арктангенса

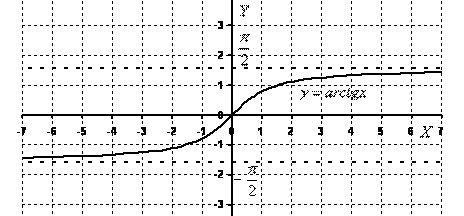
Всего лишь перевернутая ветка тангенса.
Перечислим основные свойства функции :

Область определения:

Область значений: , то есть,  функция  ограничена.
У рассматриваемой функции есть две асимптоты: , .

Арктангенс – функция нечетная: .

Самые «популярные» значения арктангенса, которые встречаются на практике, следующие: , .

К графику арккотангенса  приходится обращаться значительно реже, но, тем не менее, вот его чертеж:

Свойства арккотангенса вы вполне сможете сформулировать самостоятельно. Отмечу,  что арккотангенс, как и арккосинус, не является четной или нечетной функцией.

Пожалуй, для начала хватит. К этой странице придется частенько обращаться в ходе изучения самых различных разделов курса высшей математики.

Ну что, смертнички, полетаем? =)

Тогда надеваем парашюты и готовимся к преобразованиям графиков.

Желаю успехов!

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

Zaochnik.com – профессиональная помощь студентам,

cкидкa 15% на первый зaкaз, при оформлении введите прoмoкoд: 5530-hihi5

© Copyright  Александр Емелин, mathprofi.ru, 2010-2024, сделано в Блокноте