


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Двойные интегралы для чайников
Данный урок открывает обширную тему кратных интегралов, с которыми студенты обычно сталкиваются на втором курсе. Двойными и тройными интегралами можно запугать обывателя не хуже, чем дифференциальными уравнениями, поэтому сразу же разберёмся с вопросом: сложно или нет? Конечно, некоторым будет сложно, и, если честно, я немного слукавил с названием статьи – для того, чтобы научиться решать двойные интегралы, необходимо обладать некоторыми навыками. Во-первых, если речь идёт об интегралах, то, очевидно, придётся интегрировать. Логично. Следовательно, для освоения примеров нужно уметь находить неопределённые интегралы и вычислять определённые интегралы хотя бы на среднем уровне. Хорошая новость состоит в том, что сами по себе интегралы в большинстве случаев достаточно просты.
Кому придётся туговато? Понятное дело. Тем, кто много пил пиво в течение первых семестров. Однако нормальных студентов тоже обнадёжу – на сайте есть все материалы, чтобы восполнить пробелы или недопонимание. Просто вам придётся потратить больше времени. Ссылки на темы, которые следует изучить или повторить, будут прилагаться по ходу статьи.
На вводном уроке поэтапно и подробно будут разобраны следующие базовые моменты:
– Понятие двойного интеграла
– Область интегрирования. Порядок обхода области интегрирования. Как изменить порядок обхода?
– Как вычислить площадь плоской фигуры с помощью двойного интеграла?
После того, как вы ХОРОШО поймёте все азы, можно будет перейти к статье Как вычислить двойной интеграл? Примеры решений. Кроме того, существует распространенная задача о вычислении двойного интеграла в полярных координатах и типовое приложение о нахождении центра тяжести плоской ограниченной фигуры.
Для желающих освоить тему в максимально сжатые сроки есть компактный pdf-курс Кратные и криволинейные интегралы (3-й семестр).
И мы немедленно приступаем. Начнём с насущного вопроса – что это такое?
Понятие двойного интеграла
Двойной интеграл в общем виде записывается следующим образом:
![]()
Разбираемся в терминах и обозначениях:
![]() – значок двойного интеграла;
– значок двойного интеграла;
![]() – область интегрирования (плоская фигура);
– область интегрирования (плоская фигура);
![]() – подынтегральная функция двух переменных, часто она довольно простая;
– подынтегральная функция двух переменных, часто она довольно простая;
![]() – дифференциалы.
– дифференциалы.
Что значит вычислить двойной интеграл?
Вычислить двойной интеграл – это значит найти ЧИСЛО. Самое обычное число:
![]()
И крайне желательно найти его правильно =)
Результат (число ![]() ) может быть отрицательным. И ноль тоже запросто может получиться. Специально остановился на данном моменте, поскольку немало студентов испытывают беспокойство, когда ответ получается «шото вроде как странный».
) может быть отрицательным. И ноль тоже запросто может получиться. Специально остановился на данном моменте, поскольку немало студентов испытывают беспокойство, когда ответ получается «шото вроде как странный».
Многие помнят, что «обычный» определённый интеграл – тоже число. Здесь всё так же. У двойного интеграла существует и отличный геометрический смысл, но об этом позже, всему своё время.
Как вычислить двойной интеграл?
Для того чтобы вычислить двойной интеграл, его нужно свести к так называемым повторным интегралам. Сделать это можно двумя способами. Наиболее распространён следующий способ:
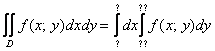
Вместо знаков вопроса необходимо расставить пределы интегрирования. Причём одиночные знаки вопроса ![]() у внешнего интеграла – это числа, а двойные знаки вопроса
у внешнего интеграла – это числа, а двойные знаки вопроса ![]() у внутреннего интеграла – это функции одной переменной
у внутреннего интеграла – это функции одной переменной ![]() , зависящие от «икс».
, зависящие от «икс».
Откуда взять пределы интегрирования? Они зависят от того, какая в условии задачи дана область ![]() . Область
. Область ![]() представляет собой обычную плоскую фигуру, с которой вы неоднократно сталкивались, например, при вычислении площади плоской фигуры или вычислении объема тела вращения. Очень скоро вы узнаете, как правильно расставлять пределы интегрирования.
представляет собой обычную плоскую фигуру, с которой вы неоднократно сталкивались, например, при вычислении площади плоской фигуры или вычислении объема тела вращения. Очень скоро вы узнаете, как правильно расставлять пределы интегрирования.
После того, как переход к повторным интегралам осуществлён, следуют непосредственно вычисления: сначала берётся внутренний интеграл 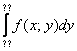 , а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.
, а потом – внешний. Друг за другом. Отсюда и название – повторные интегралы.
Грубо говоря, задача сводится к вычислению двух определённых интегралов. Как видите всё не так сложно и страшно, и если вы совладали с «обыкновенным» определённым интегралом, что мешает разобраться с двумя интегралами?!
Второй способ перехода к повторным интегралам встречается несколько реже:
![]()
Что поменялось? Поменялся порядок интегрирования: теперь внутренний интеграл берётся по «икс», а внешний – по «игрек». Пределы интегрирования, обозначенные звёздочками – будут другими! Одиночные звёздочки внешнего интеграла – это числа, а двойные звёздочки внутреннего интеграла – это обратные функции ![]() , зависящие от «игрек».
, зависящие от «игрек».
Какой бы мы ни выбрали способ перехода к повторным интегралам, окончательный ответ обязательно получится один и тот же:
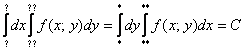
Пожалуйста, запомните это важное свойство, которое можно использовать, в том числе, для проверки решения.
Алгоритм решения двойного интеграла:
Систематизируем информацию: в каком порядке нужно решать рассматриваемую задачу?
1) Выполнить чертёж. Без него решить задачу практически невозможо. За исключением каких-то совсем простых случаев и за исключением вундеркиндов, умеющих играть в шахматы «вслепую». На чертеже следует изобразить область ![]() , которая представляет собой плоскую фигуру. Чаще всего фигура незамысловата и ограничена какими-нибудь прямыми, параболами, гиперболами и т. д. Грамотную и быструю технику построения графиков можно освоить на уроках Графики и основные свойства элементарных функций, Геометрические преобразования графиков.
, которая представляет собой плоскую фигуру. Чаще всего фигура незамысловата и ограничена какими-нибудь прямыми, параболами, гиперболами и т. д. Грамотную и быструю технику построения графиков можно освоить на уроках Графики и основные свойства элементарных функций, Геометрические преобразования графиков.
2) Расставить пределы интегрирования и перейти к повторным интегралам.
3) Взять внутренний интеграл
4) Взять внешний интеграл и получить ответ (число).
Область интегрирования. Порядок обхода области интегрирования.
Как изменить порядок обхода?
В данном параграфе мы рассмотрим важнейший вопрос – как перейти к повторным интегралам и правильно расставить пределы интегрирования. Как было сказано выше, сделать это можно так:
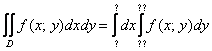
И так:
![]()
На практике эта вроде бы несложная задача вызывает наибольшие затруднения, и студенты часто путаются в расстановке пределов интегрирования. Рассмотрим конкретный пример:
Пример 1
Дан двойной интеграл ![]() с областью интегрирования
с областью интегрирования ![]() . Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
. Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
Решение: изобразим область интегрирования на чертеже:
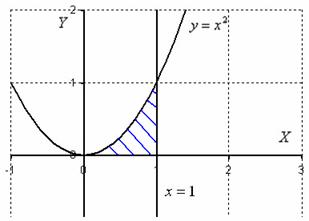
Обычная плоская фигура и ничего особенного.
Теперь я выдам каждому из вас орудие труда – палку-копалку лазерную указку. Задача состоит в том, чтобы просканировать лучом лазера каждую точку заштрихованной области:
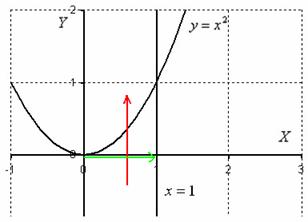
Луч лазера проходит область интегрирования строго снизу вверх, то есть указку вы ВСЕГДА держите ниже плоской фигуры. Луч входит в область через ось абсцисс, которая задаётся уравнением ![]() и выходит из области через параболу
и выходит из области через параболу ![]() (красная стрелка). Чтобы просветить всю область, вам нужно строго слева направо провести указкой вдоль оси
(красная стрелка). Чтобы просветить всю область, вам нужно строго слева направо провести указкой вдоль оси ![]() от 0 до 1 (зелёная стрелка).
от 0 до 1 (зелёная стрелка).
Итак, что получилось:
«игрек» изменяется от 0 до ![]() ;
;
«икс» изменяется от 0 до 1.
В задачах вышесказанное записывают в виде неравенств:
![]()
Данные неравенства называют порядком обхода области интегрирования или просто порядком интегрирования
После того, как мы разобрались с порядком обхода, можно перейти от двойного интеграла к повторным интегралам:
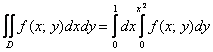
Половина задачи решена. Теперь нужно перейти к повторным интегралам вторым способом. Для этого следует найти обратные функции. Кто ознакомился со вторым параграфом урока Объем тела вращения, тому будет легче. Смотрим на функции, которыми задается область ![]() . Если совсем просто, то перейти к обратным функциям, это значит – выразить «иксы» через «игреки». Единственной функцией, где есть и «икс» и «игрек», является
. Если совсем просто, то перейти к обратным функциям, это значит – выразить «иксы» через «игреки». Единственной функцией, где есть и «икс» и «игрек», является ![]() .
.
Если ![]() , то
, то ![]() , причём:
, причём:
обратная функция ![]() задает правую ветку параболы;
задает правую ветку параболы;
обратная функция ![]() задает левую ветку параболы.
задает левую ветку параболы.
Нередко возникают сомнения, вот, к примеру, функция ![]() определяет левую или правую ветвь параболы? Сомнения развеять очень просто: возьмите какую-нибудь точку параболы окромя вершины, например,
определяет левую или правую ветвь параболы? Сомнения развеять очень просто: возьмите какую-нибудь точку параболы окромя вершины, например, ![]() (с правой ветви) и подставьте её координаты в любое уравнение, например, в то же уравнение
(с правой ветви) и подставьте её координаты в любое уравнение, например, в то же уравнение ![]() :
:
![]()
Получено верное равенство, значит, функция ![]() определяет именно правую ветвь параболы, а не левую.
определяет именно правую ветвь параболы, а не левую.
Более того, данную проверку (мысленно или на черновике) желательно проводить всегда, после того, как вы перешли к обратным функциям. Времени займет всего ничего, а от ошибки убережёт наверняка!
Обходим область интегрирования вторым способом:
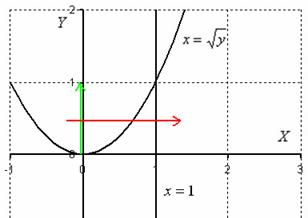
Теперь лазерную указку держим слева от области интегрирования. Луч лазера проходит область строго слева направо. В данном случае он входит в область через ветвь параболы ![]() и выходит из области через прямую, которая задана уравнением
и выходит из области через прямую, которая задана уравнением ![]() (красная стрелка). Чтобы просканировать лазером всю область, нужно провести указкой вдоль оси
(красная стрелка). Чтобы просканировать лазером всю область, нужно провести указкой вдоль оси ![]() строго снизу вверх от 0 до 1 (зеленая стрелка).
строго снизу вверх от 0 до 1 (зеленая стрелка).
Таким образом:
«икс» изменяется от ![]() до 1;
до 1;
«игрек» изменяется от 0 до 1.
Порядок обхода области следует записать в виде неравенств:
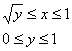
И, следовательно, переход к повторным интегралам таков:
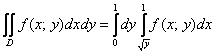
Ответ можно записать следующим образом:
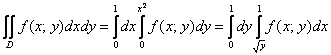
Еще раз напоминаю, что окончательный результат вычислений не зависит от того, какой порядок обхода области мы выбрали (поэтому поставлен знак равенства). Но, до конечного результата ещё далеко, сейчас наша задача – лишь правильно расставить пределы интегрирования.
Пример 2
Дан двойной интеграл ![]() с областью интегрирования
с областью интегрирования ![]() . Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
. Перейти к повторным интегралам и расставить пределы интегрирования двумя способами.
Это пример для самостоятельного решения. Грамотно постройте чертёж и строго соблюдайте направления обхода (откуда и куда светить лазерной указкой). Примерный образец чистового оформления в конце урока.
Чаще всего типовое задание встречается немного в другой формулировке:
Пример 3
Построить область интегрирования и изменить порядок интегрирования
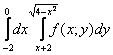
Решение: по условию дан первый способ обхода области. Решение опять начинается с чертежа. Здесь область ![]() не лежит на блюдечке с голубой каёмочкой, но построить её не составляет особого труда. Сначала «снимаем» функции с пределов интегрирования:
не лежит на блюдечке с голубой каёмочкой, но построить её не составляет особого труда. Сначала «снимаем» функции с пределов интегрирования: ![]() ,
, ![]() . Функция
. Функция ![]() , понятно, задаёт прямую, но что задаёт функция
, понятно, задаёт прямую, но что задаёт функция ![]() ? Давайте её немного преобразуем:
? Давайте её немного преобразуем:
![]() – окружность с центром в начале координат радиуса 2. Функция же
– окружность с центром в начале координат радиуса 2. Функция же ![]() задаёт верхнюю полуокружность (не забываем, что если есть сомнения, то всегда можно подставить точку лежащую на верхней или нижней полуокружности).
задаёт верхнюю полуокружность (не забываем, что если есть сомнения, то всегда можно подставить точку лежащую на верхней или нижней полуокружности).
Смотрим на пределы внешнего интеграла: «икс» изменяется от –2 до 0.
Выполним чертёж:
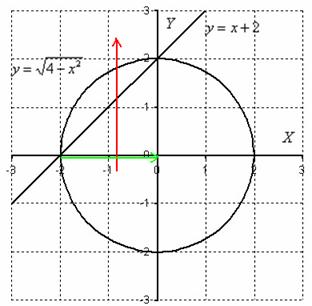
Для наглядности я указал стрелками первый способ обхода области, который соответствует повторным интегралам условия: 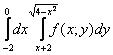 .
.
Теперь нужно изменить порядок обхода области, для этого перейдем к обратным функциям (выразим «иксы» через «игреки»):
![]()
Недавно мы преобразовали функцию ![]() к уравнению окружности
к уравнению окружности ![]() , далее выражаем «икс»:
, далее выражаем «икс»: ![]()
В результате получаем две обратные функции:
![]() – определяет правую полуокружность;
– определяет правую полуокружность;
![]() – определяет левую полуокружность.
– определяет левую полуокружность.
Опять же, если возникают сомнения, возьмите любую точку окружности (кроме верхней и нижней) и выясните, где лево, а где право.
Изменим порядок обхода области:
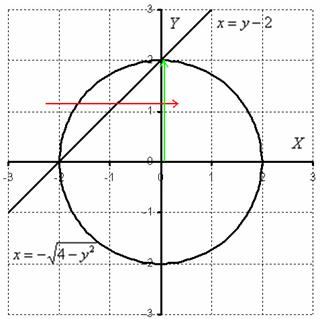
Согласно второму способу обхода, лазерный луч входит в область слева через левую полуокружность ![]() и выходит справа через прямую
и выходит справа через прямую ![]() (красная стрелка). В то же время лазерная указка проводится вдоль оси ординат снизу вверх от 0 до 2 (зелёная стрелка).
(красная стрелка). В то же время лазерная указка проводится вдоль оси ординат снизу вверх от 0 до 2 (зелёная стрелка).
Таким образом, порядок обхода области:
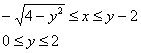
В общем-то, можно записать ответ:
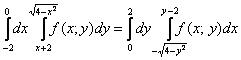
Пример 4
Построить область интегрирования и изменить порядок интегрирования
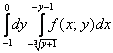
Это пример для самостоятельного решения. Пример не очень сложный, но обратите внимание, что порядок обхода изначально задан вторым способом! Что делать в подобных случаях? Во-первых, возникает трудность с чертежом, поскольку чертить график обратной функции наподобие ![]() непривычно даже мне самому. Я рекомендую следующий порядок действий: сначала из
непривычно даже мне самому. Я рекомендую следующий порядок действий: сначала из ![]() получаем «обычную» функцию (выражаем «игрек» через «икс»). Далее строим график этой «обычной» функции (всегда можно построить хотя бы поточечно). Аналогично поступаем с более простой линейной функцией: из
получаем «обычную» функцию (выражаем «игрек» через «икс»). Далее строим график этой «обычной» функции (всегда можно построить хотя бы поточечно). Аналогично поступаем с более простой линейной функцией: из ![]() выражаем «игрек» и проводим прямую.
выражаем «игрек» и проводим прямую.
Анализируем исходные пределы интегрирования: входим слева в область через ![]() и выходим через
и выходим через ![]() . При этом все дела происходят в «игрековой» полосе от –1 до 0. После того, как вы определили на чертеже область интегрирования, сменить порядок обхода не составит особого труда. Примерный образец оформления решения в конце урока.
. При этом все дела происходят в «игрековой» полосе от –1 до 0. После того, как вы определили на чертеже область интегрирования, сменить порядок обхода не составит особого труда. Примерный образец оформления решения в конце урока.
Похожий пример я еще разберу подробнее чуть позже.
Даже если вы всё отлично поняли, пожалуйста, не торопитесь переходить непосредственно к вычислениям двойного интеграла. Порядок обхода – вещь коварная, и очень важно немного набить руку на данной задаче, тем более, я еще не всё рассмотрел!
В предыдущих четырёх примерах область интегрирования находилась целиком в 1-й, 2-й, 3-й и 4-й координатных четвертях. Всегда ли это так? Нет, естественно.
Пример 5
Изменить порядок интегрирования
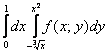
Решение: выполним чертёж, при этом, график функции ![]() фактически представляет собой кубическую параболу, просто она «лежит на боку»:
фактически представляет собой кубическую параболу, просто она «лежит на боку»:
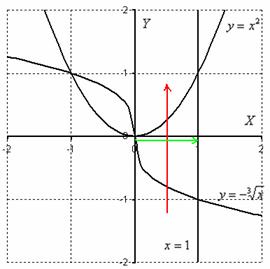
Порядок обхода области, который соответствует повторным интегралам 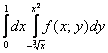 , обозначен стрелками. Обратите внимание, что в ходе выполнения чертежа прорисовалась еще одна ограниченная фигура (левее оси ординат). Поэтому следует быть внимательным при определении области интегрирования – за область можно ошибочно принять не ту фигуру.
, обозначен стрелками. Обратите внимание, что в ходе выполнения чертежа прорисовалась еще одна ограниченная фигура (левее оси ординат). Поэтому следует быть внимательным при определении области интегрирования – за область можно ошибочно принять не ту фигуру.
Перейдем к обратным функциям:
![]() – нужная нам правая ветвь параболы;
– нужная нам правая ветвь параболы;
![]()
Изменим порядок обхода области. Как вы помните, при втором способе обхода, область нужно сканировать лазерным лучом слева направо. Но тут наблюдается интересная вещь:
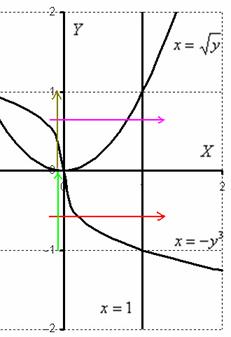
Как поступать в подобных случаях? В таких случаях следует разделить область интегрирования на две части и для каждой из частей составить свои повторные интегралы:
1) Если «игрек» изменяется от –1 до 0 (зеленая стрелка), то луч входит в область через кубическую параболу ![]() и выходит через прямую
и выходит через прямую ![]() (красная стрелка). Поэтому порядок обхода области будет следующим:
(красная стрелка). Поэтому порядок обхода области будет следующим:
![]()
И соответствующие повторные интегралы:
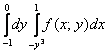
2) Если «игрек» изменяется от 0 до 1 (коричневая стрелка), то луч входит в область через ветвь параболы ![]() и выходит через ту же прямую
и выходит через ту же прямую ![]() (малиновая стрелка). Следовательно, порядок обхода области будет следующим:
(малиновая стрелка). Следовательно, порядок обхода области будет следующим:
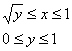
И соответствующие повторные интегралы:
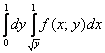
У определенных и кратных интегралов есть весьма удобное свойство аддитивности, то есть их можно сложить, что в данном случае и следует сделать:
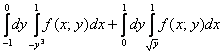 – а вот и наш обход области вторым способом в виде суммы двух интегралов.
– а вот и наш обход области вторым способом в виде суммы двух интегралов.
Ответ записываем так:
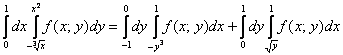
Какой порядок обхода выгоднее? Конечно тот, который был дан в условии задачи – вычислений будет в два раза меньше!
Пример 6
Изменить порядок интегрирования
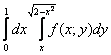
Это пример для самостоятельного решения. В нём присутствуют полуокружности, разборки с которыми были подробно рассмотрены в Примере 3. Примерный образец оформления решения в конце урока.
А сейчас обещанная задача, когда изначально задан второй способ обхода области:
Пример 7
Изменить порядок интегрирования
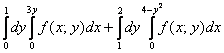
Решение: когда порядок обхода задан вторым способом, то перед построением чертежа целесообразно перейти к «обычным» функциям. В данном примере присутствуют два пациента для преобразования: ![]() и
и ![]() .
.
С линейной функцией всё просто: ![]()
График функции ![]() представляется собой параболу с претензией на каноничность.
представляется собой параболу с претензией на каноничность.
Выразим «игрек» через «икс»:
![]()
Получаем две ветви параболы: ![]() и
и ![]() . Какую из них выбрать? Проще всего сразу выполнить чертёж. И даже если вы крепко позабыли материал аналитической геометрии о параболе, то всё равно обе ветви можно построить поточечно:
. Какую из них выбрать? Проще всего сразу выполнить чертёж. И даже если вы крепко позабыли материал аналитической геометрии о параболе, то всё равно обе ветви можно построить поточечно:
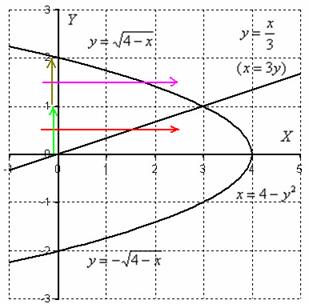
Еще раз обращаю внимание на тот факт, что на данном чертеже получилось несколько плоских фигур, и очень важно выбрать нужную фигуру! В выборе искомой фигуры как раз помогут пределы интегрирования исходных интегралов:
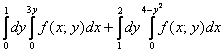 , при этом не забывайте, что обратная функция
, при этом не забывайте, что обратная функция ![]() задаёт всю параболу.
задаёт всю параболу.
Стрелочки, которыми обозначен обход фигуры, в точности соответствуют пределам интегрирования интегралов 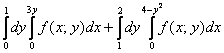 .
.
Довольно быстро вы научитесь проводить такой анализ мысленно и находить нужную область интегрирования.
Когда фигура найдена, заключительная часть решения, в общем-то, очень проста, меняем порядок обхода области:
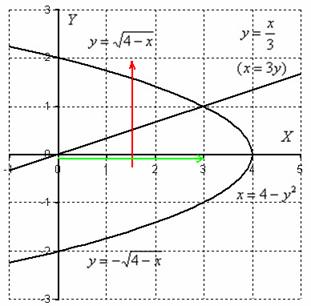
Обратные функции уже найдены, и требуемый порядок обхода области:
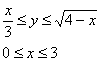
Ответ: 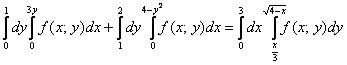
Заключительный пример параграфа для самостоятельного решения:
Пример 8
Изменить порядок интегрирования
![]()
Полное решение и ответ в конце урока.
Как вычислить площадь плоской фигуры с помощью двойного интеграла?
Начинаем рассматривать собственно процесс вычисления двойного интеграла ![]() и знакомиться с его геометрическим смыслом.
и знакомиться с его геометрическим смыслом.
Двойной интеграл ![]() численно равен площади плоской фигуры
численно равен площади плоской фигуры ![]() (области интегрирования). Это простейший вид двойного интеграла, когда функция двух переменных равна единице:
(области интегрирования). Это простейший вид двойного интеграла, когда функция двух переменных равна единице: ![]() .
.
Сначала рассмотрим задачу в общем виде. Сейчас вы немало удивитесь, насколько всё действительно просто! Вычислим площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() . Для определённости считаем, что
. Для определённости считаем, что ![]() на отрезке
на отрезке ![]() . Площадь данной фигуры численно равна:
. Площадь данной фигуры численно равна:
![]()
Изобразим область ![]() на чертеже:
на чертеже:
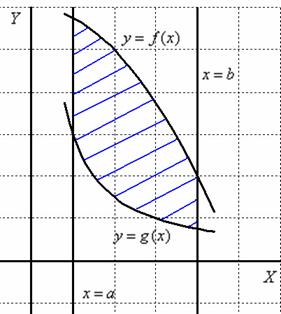
Выберем первый способ обхода области:
![]()
Таким образом: 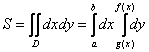
И сразу важный технический приём: повторные интегралы можно считать по отдельности. Сначала внутренний интеграл, затем – внешний интеграл. Данный способ настоятельно рекомендую начинающим в теме чайникам.
1) Вычислим внутренний интеграл, при этом интегрирование проводится по переменной «игрек»:
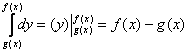
Неопределённый интеграл тут простейший, и далее используется банальная формула Ньютона-Лейбница, с той лишь разницей, что пределами интегрирования являются не числа, а функции. Сначала подставили в «игрек» (первообразную функцию) верхний предел, затем – нижний предел
2) Результат, полученный в первом пункте нужно подставить во внешний интеграл:
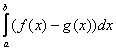
Более компактная запись всего решения выглядит так:
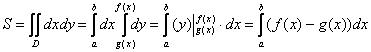
Полученная формула 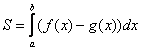 – это в точности рабочая формула для вычисления площади плоской фигуры с помощью «обычного» определённого интеграла! Смотрите урок Вычисление площади с помощью определенного интеграла, там она на каждом шагу!
– это в точности рабочая формула для вычисления площади плоской фигуры с помощью «обычного» определённого интеграла! Смотрите урок Вычисление площади с помощью определенного интеграла, там она на каждом шагу!
То есть задача вычисления площади с помощью двойного интеграла мало чем отличается от задачи нахождения площади с помощью определённого интеграла! Фактически это одно и тоже!
Соответственно, никаких трудностей возникнуть не должно! Я рассмотрю не очень много примеров, так как вы, по сути, неоднократно сталкивались с данной задачей.
Пример 9
С помощью двойного интеграла вычислить площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]()
Решение: изобразим область ![]() на чертеже:
на чертеже:
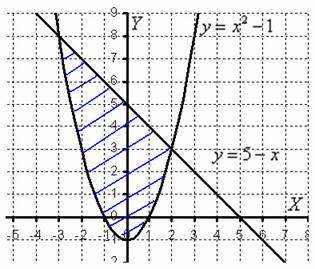
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Выберем следующий порядок обхода области:
![]()
Здесь и далее я не буду останавливаться на том, как выполнять обход области, поскольку в первом параграфе были приведены очень подробные разъяснения.
Таким образом:
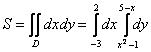
Как я уже отмечал, начинающим лучше вычислять повторные интегралы по отдельности, этого же метода буду придерживаться и я:
1) Сначала с помощью формулы Ньютона-Лейбница разбираемся с внутренним интегралом:
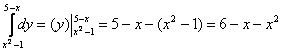
2) Результат, полученный на первом шаге, подставляем во внешний интеграл:
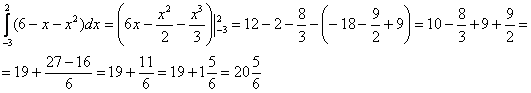
Пункт 2 – фактически нахождение площади плоской фигуры с помощью определённого интеграла.
Ответ: ![]()
Вот такая вот глупая и наивная задача.
Любопытный пример для самостоятельного решения:
Пример 10
С помощью двойного интеграла вычислить площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]() ,
, ![]()
Примерный образец чистового оформления решения в конце урока.
В Примерах 9-10 значительно выгоднее использовать первый способ обхода области, любознательные читатели, кстати, могут изменить порядок обхода и вычислить площади вторым способом. Если не допустите ошибку, то, естественно, получатся те же самые значения площадей.
Но в ряде случаев более эффективен второй способ обхода области, и в заключение курса молодого ботана рассмотрим ещё пару примеров на эту тему:
Пример 11
С помощью двойного интеграла, вычислить площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]() ,
, ![]()
Решение: нас с нетерпением ждут две параболы, которые лежат на боку.
Как проще всего сделать чертёж?
Представим параболу ![]() в виде двух функций:
в виде двух функций:
![]() – верхняя ветвь и
– верхняя ветвь и ![]() – нижняя ветвь.
– нижняя ветвь.
Аналогично, представим параболу ![]() в виде верхней
в виде верхней ![]() и нижней
и нижней ![]() ветвей.
ветвей.
Далее рулит поточечное построение графиков, в результате чего получается вот такая причудливая фигура:
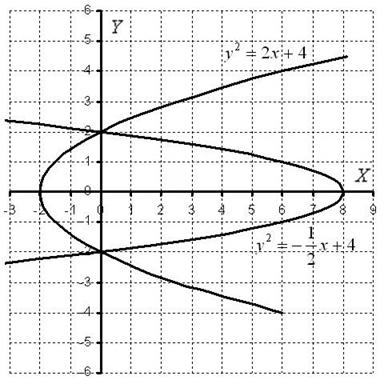
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Что будет, если мы выберем первый способ обхода области? Во-первых, данную область придётся разделить на две части. А во-вторых, мы будем наблюдать сию печальную картину: 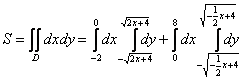 . Интегралы, конечно, не сверхсложного уровня, но… существует старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.
. Интегралы, конечно, не сверхсложного уровня, но… существует старая математическая присказка: кто с корнями дружен, тому зачёт не нужен.
Поэтому из недоразумения, которое дано в условии, выразим обратные функции:
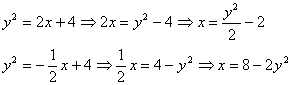
Обратные функции в данном примере обладают тем преимуществом, что задают сразу всю параболу целиком без всяких там листьев, желудей веток и корней.
Согласно второму способу, обход области будет следующим:
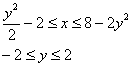
Таким образом:
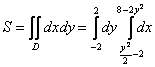
Как говорится, ощутите разницу.
1) Расправляемся с внутренним интегралом:
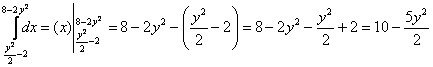
Результат подставляем во внешний интеграл:
2)
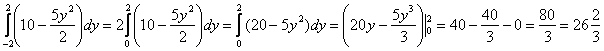
Интегрирование по переменной «игрек» не должно смущать, была бы буква «зю» – замечательно бы проинтегрировалось и по ней. Хотя кто прочитал второй параграф урока Как вычислить объем тела вращения, тот уже не испытывает ни малейшей неловкости с интегрированием по «игрек».
Также обратите внимание на первый шаг: подынтегральная функция ![]() является чётной, а отрезок интегрирования симметричен относительно нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Данный приём подробно закомментирован на уроке Эффективные методы вычисления определённого интеграла.
является чётной, а отрезок интегрирования симметричен относительно нуля. Поэтому отрезок можно споловинить, а результат – удвоить. Данный приём подробно закомментирован на уроке Эффективные методы вычисления определённого интеграла.
Что добавить…. Всё!
Ответ: ![]()
Для проверки своей техники интегрирования можете попробовать вычислить 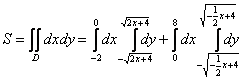 . Ответ должен получиться точно таким же.
. Ответ должен получиться точно таким же.
Пример 12
С помощью двойного интеграла, вычислить площадь плоской фигуры ![]() , ограниченной линиями
, ограниченной линиями ![]()
Это пример для самостоятельного решения. Интересно отметить, что если вы попробуете использовать первый способ обхода области, то фигуру придётся разделить уже не на две, а на три части! И, соответственно, получится три пары повторных интегралов. Бывает и такое.
Мастер класс подошел к завершению, и пора переходить на гроссмейстерский уровень – Как вычислить двойной интеграл? Примеры решений. Постараюсь во второй статье так не маньячить =)
Желаю успехов!
Решения и ответы:
Пример 2. Решение: изобразим область ![]() на чертеже:
на чертеже:
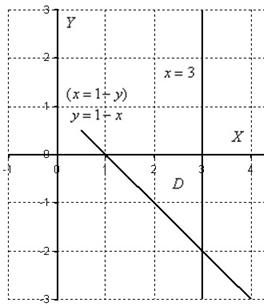
Выберем следующий порядок обхода области:
![]()
Таким образом: 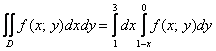
Перейдём к обратным функциям: ![]()
Изменим порядок обхода области:
![]()
Таким образом: 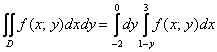
Ответ: 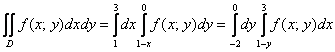
Пример 4. Решение: перейдём к прямым функциям:
![]()
![]()
Выполним чертёж:
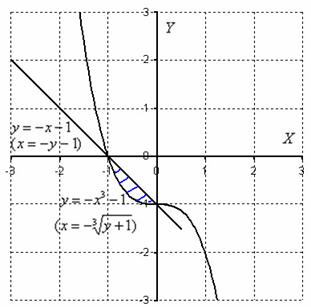
Изменим порядок обхода области:
![]()
Ответ: 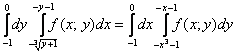
Пример 6. Решение: выполним чертеж:
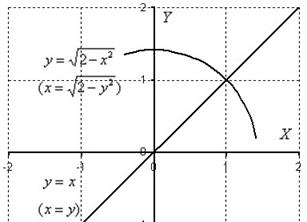
Перейдем к обратным функциям:
![]()
![]()
Изменим порядок интегрирования, разделив область интегрирования на две части. При этом порядок обхода области:
1) ![]() , 2)
, 2) 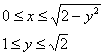
Ответ: 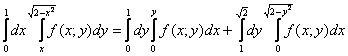
Пример 8. Решение: изобразим область интегрирования на чертеже:
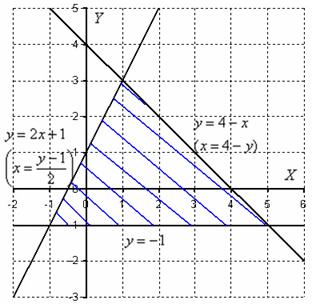
Перейдём к обратным функциям:
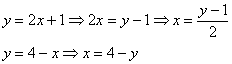
Изменим порядок обхода области:
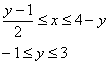
Ответ: 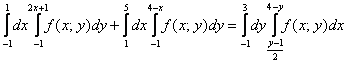
Пример 10. Решение: изобразим область ![]() на чертеже:
на чертеже:
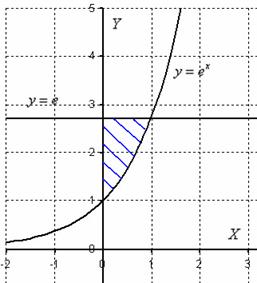
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Выберем следующий порядок обхода области:
![]()
Таким образом: 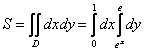
1) 
2) 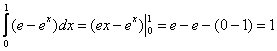
Ответ: ![]()
Пример 12. Решение: изобразим данную фигуру на чертеже:
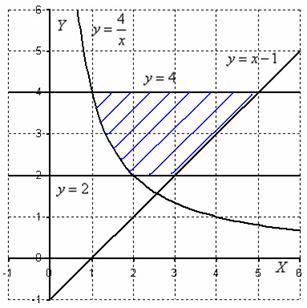
Площадь фигуры вычислим с помощью двойного интеграла по формуле:
![]()
Перейдём к обратным функциям:
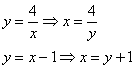
Порядок обхода области:
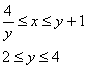
Таким образом:
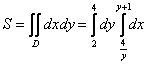
1) 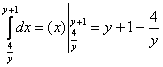
2)
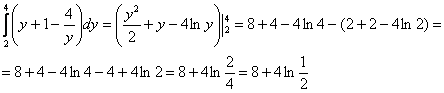
Ответ: ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright