


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Взаимное расположение прямых в пространстве.
Задачи с прямой в пространстве
Данная статья – это вторая часть урока Уравнения в прямой пространстве. Не прошло и минуты, как я создал новый вёрдовский файл и продолжил столь увлекательную тему. Нужно ловить моменты рабочего настроя, поэтому лирического вступления не будет. Будет прозаическая порка =):
- Взаимное расположение прямых в пространстве
- Скрещивающиеся прямые
- Как найти уравнения прямой, содержащей общий перпендикуляр?
- Как найти расстояние между скрещивающимися прямыми?
- Пересекающиеся прямые в пространстве
- Как построить прямую пространства, перпендикулярную данной?
- Как найти расстояние от точки до прямой в пространстве?
- Как найти угол между прямыми в пространстве?
- Параллельные прямые в пространстве
Взаимное расположение прямых в пространстве
Две прямые ![]() пространства могут:
пространства могут:
1) скрещиваться;
2) пересекаться в точке ![]() ;
;
3) быть параллельными ![]() ;
;
4) совпадать.
Случай № 1 принципиально отличается от других случаев. Две прямые скрещиваются, если они не лежат в одной плоскости. Поднимите одну руку вверх, а другую руку вытяните вперёд – вот вам и пример скрещивающихся прямых. В пунктах же № 2-4 прямые обязательно лежат в одной плоскости.
Как выяснить взаимное расположение прямых в пространстве?
Рассмотрим две прямые пространства:
– прямую ![]() , заданную точкой
, заданную точкой ![]() и направляющим вектором
и направляющим вектором ![]() ;
;
– прямую ![]() , заданную точкой
, заданную точкой ![]() и направляющим вектором
и направляющим вектором ![]() .
.
Для лучшего понимания выполним схематический чертёж:
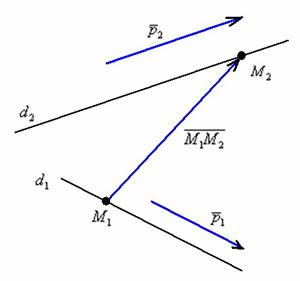
На чертеже в качестве примера изображены скрещивающиеся прямые.
Как разобраться с этими прямыми?
Так как известны точки ![]() , то легко найти вектор
, то легко найти вектор ![]() .
.
Если прямые скрещиваются, то векторы ![]() не компланарны, а значит, определитель, составленный из их координат, ненулевой. Или, что фактически то же самое, смешанное произведение векторов будет отлично от нуля:
не компланарны, а значит, определитель, составленный из их координат, ненулевой. Или, что фактически то же самое, смешанное произведение векторов будет отлично от нуля: ![]() .
.
В случаях № 2-4 наша конструкция «падает» в одну плоскость, при этом векторы ![]() компланарны, а смешанное произведение линейно зависимых векторов равняется нулю:
компланарны, а смешанное произведение линейно зависимых векторов равняется нулю: ![]() .
.
Раскручиваем алгоритм дальше. Предположим, что ![]() , следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.
, следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.
Если направляющие векторы ![]() не коллинеарны, то прямые пересекаются. Как проверить два вектора на коллинеарность, подробно рассмотрено в той же статье Линейная (не) зависимость векторов. Базис векторов.
не коллинеарны, то прямые пересекаются. Как проверить два вектора на коллинеарность, подробно рассмотрено в той же статье Линейная (не) зависимость векторов. Базис векторов.
Если направляющие векторы ![]() коллинеарны, то прямые либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в уравнение второй прямой; если координаты «подошли», то прямые совпадают, если «не подошли», то прямые параллельны.
коллинеарны, то прямые либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в уравнение второй прямой; если координаты «подошли», то прямые совпадают, если «не подошли», то прямые параллельны.
Ход алгоритма незатейлив, но практические примеры всё равно не помешают:
Пример 11
Выяснить взаимное расположение двух прямых
![]()
Решение: как и во многих задачах геометрии, решение удобно оформить по пунктам:
1) Вытаскиваем из уравнений точки и направляющие векторы:
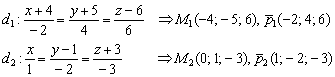
2) Найдём вектор ![]() .
.
3) Вычислим смешанное произведение векторов:
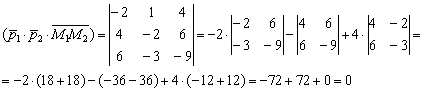
Таким образом, векторы ![]() компланарны, а значит, прямые
компланарны, а значит, прямые ![]() лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.
лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.
4) Проверим направляющие векторы ![]() на коллинеарность.
на коллинеарность.
Составим систему из соответствующих координат данных векторов:
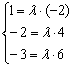
Из каждого уравнения следует, что ![]() , следовательно, система совместна, соответствующие координаты векторов пропорциональны и векторы коллинеарны.
, следовательно, система совместна, соответствующие координаты векторов пропорциональны и векторы коллинеарны.
Вывод: прямые ![]() параллельны либо совпадают.
параллельны либо совпадают.
5) Выясним, есть ли у прямых общие точки. Возьмём очевидную точку ![]() , принадлежащую первой прямой, и подставим её координаты в уравнения прямой
, принадлежащую первой прямой, и подставим её координаты в уравнения прямой ![]() :
:
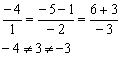
Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть параллельными.
Ответ: ![]()
Интересный пример для самостоятельного решения:
Пример 12
Выяснить взаимное расположение прямых
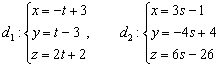
Обратите внимание, что у второй прямой в качестве параметра выступает буква ![]() . Логично. В общем случае – это же две различные прямые, поэтому у каждой прямой свой параметр.
. Логично. В общем случае – это же две различные прямые, поэтому у каждой прямой свой параметр.
И снова призываю не пропускать примеры, пороть буду предлагаемые мной задачи далеко не случайны ;-)
Задачи с прямой в пространстве
В заключительной части урока я постараюсь рассмотреть максимальное количество различных задач с пространственными прямыми. При этом будет соблюдён начатый порядок повествования: сначала мы рассмотрим задачи со скрещивающимися прямыми, затем с пересекающимися прямыми, и в конце поговорим о параллельных прямых в пространстве. Однако должен сказать, что некоторые задачи данного урока можно сформулировать сразу для нескольких случаев расположения прямых, и в этой связи разбиение раздела на параграфы несколько условно. Есть более простые примеры, есть более сложные примеры, и, надеюсь, каждый найдёт то, что нужно.
Скрещивающиеся прямые
Напоминаю, что прямые скрещиваются, если не существует плоскости, в которой бы они обе лежали. И я рад представить вашему вниманию дракона с четырьмя головами:
Пример 13
Даны прямые ![]() . Требуется:
. Требуется:
а) доказать, что прямые скрещиваются;
б) найти уравнения прямой ![]() , проходящей через точку
, проходящей через точку ![]() перпендикулярно данным прямым;
перпендикулярно данным прямым;
в) составить уравнения прямой ![]() , которая содержит общий перпендикуляр скрещивающихся прямых;
, которая содержит общий перпендикуляр скрещивающихся прямых;
г) найти расстояние ![]() между прямыми.
между прямыми.
Решение осилит идущий:
а) Докажем, что прямые скрещиваются. Найдём точки и направляющие векторы данных прямых:
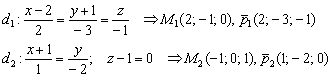
Найдём вектор: ![]()
Вычислим смешанное произведение векторов:
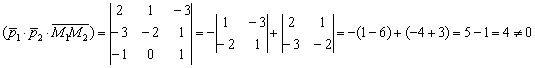
Таким образом, векторы ![]() не компланарны, а значит, прямые
не компланарны, а значит, прямые ![]() скрещиваются, что и требовалось доказать.
скрещиваются, что и требовалось доказать.
Наверное, все уже давно подметили, что для скрещивающихся прямых алгоритм проверки получается короче всего.
б) Найдём уравнения прямой ![]() , которая проходит через точку
, которая проходит через точку ![]() и перпендикулярна прямым
и перпендикулярна прямым ![]() . Выполним схематический чертёж:
. Выполним схематический чертёж:
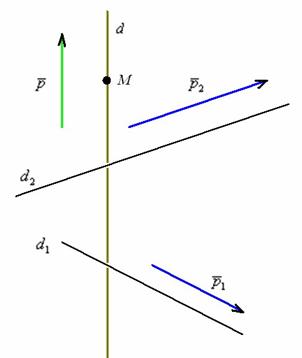
Для разнообразия я разместил прямую ![]() ЗА прямыми
ЗА прямыми ![]() , посмотрИте, как она немного стёрта в точках скрещивания. Скрещивания? Да, в общем случае прямая «дэ» будет скрещиваться с исходными прямыми. Хотя данный момент нас пока не интересует, надо просто построить перпендикулярную прямую и всё.
, посмотрИте, как она немного стёрта в точках скрещивания. Скрещивания? Да, в общем случае прямая «дэ» будет скрещиваться с исходными прямыми. Хотя данный момент нас пока не интересует, надо просто построить перпендикулярную прямую и всё.
Что известно о прямой «дэ»? Известна принадлежащая ей точка ![]() . Не хватает направляющего вектора.
. Не хватает направляющего вектора.
По условию прямая ![]() должна быть перпендикулярна прямым
должна быть перпендикулярна прямым ![]() , а значит, её направляющий вектор
, а значит, её направляющий вектор ![]() будет ортогонален направляющим векторам
будет ортогонален направляющим векторам ![]() . Уже знакомый из Примера № 9 мотив, найдём векторное произведение:
. Уже знакомый из Примера № 9 мотив, найдём векторное произведение:
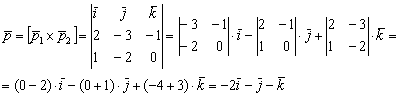
Составим уравнения прямой «дэ» по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]()
Готово. В принципе, можно сменить знаки в знаменателях и записать ответ в виде ![]() , но надобности в этом особой нет.
, но надобности в этом особой нет.
Для проверки нужно подставить координаты точки ![]() в полученные уравнения прямой, затем с помощью скалярного произведения векторов убедиться, что вектор
в полученные уравнения прямой, затем с помощью скалярного произведения векторов убедиться, что вектор ![]() действительно ортогонален направляющим векторам «пэ один» и «пэ два».
действительно ортогонален направляющим векторам «пэ один» и «пэ два».
Как найти уравнения прямой, содержащей общий перпендикуляр?
в) Эта задачка посложнее будет. Чайникам рекомендую пропустить данный пункт, не хочу охлаждать вашу искреннюю симпатию к аналитической геометрии =) Кстати, и более подготовленным читателям, возможно, лучше тоже повременить, дело в том, что по сложности пример надо бы поставить последним в статье, но по логике изложения он должен располагаться здесь.
Итак, требуется найти уравнения прямой ![]() , которая содержит общий перпендикуляр скрещивающихся прямых.
, которая содержит общий перпендикуляр скрещивающихся прямых.
Общий перпендикуляр скрещивающихся прямых – это отрезок, соединяющий данные прямые и перпендикулярный данным прямым:
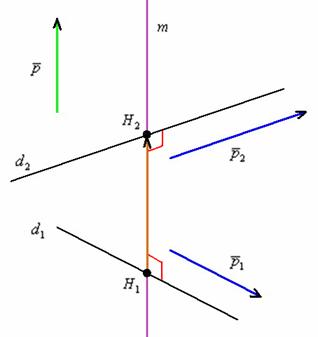
Вот наш красавец: ![]() – общий перпендикуляр скрещивающихся прямых
– общий перпендикуляр скрещивающихся прямых ![]() . Он единственный. Другого такого нет. Нам же требуется составить уравнения прямой
. Он единственный. Другого такого нет. Нам же требуется составить уравнения прямой ![]() , которая содержит данный отрезок.
, которая содержит данный отрезок.
Что известно о прямой «эм»? Известен её направляющий вектор ![]() , найденный в предыдущем пункте. Но, к сожалению, мы не знаем ни одной точки, принадлежащей прямой «эм», не знаем и концов перпендикуляра – точек
, найденный в предыдущем пункте. Но, к сожалению, мы не знаем ни одной точки, принадлежащей прямой «эм», не знаем и концов перпендикуляра – точек ![]() . Где эта перпендикулярная прямая пересекает две исходные прямые? В Африке, в Антарктиде? Из первоначального обзора и анализа условия вообще не видно, как решать задачу…. Но есть хитрый ход, связанный с использованием параметрических уравнений прямой.
. Где эта перпендикулярная прямая пересекает две исходные прямые? В Африке, в Антарктиде? Из первоначального обзора и анализа условия вообще не видно, как решать задачу…. Но есть хитрый ход, связанный с использованием параметрических уравнений прямой.
Решение оформим по пунктам:
1) Перепишем уравнения первой прямой в параметрической форме:
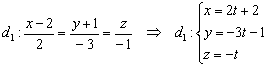
Рассмотрим точку ![]() . Координат мы не знаем. НО. Если точка принадлежит данной прямой, то её координатам
. Координат мы не знаем. НО. Если точка принадлежит данной прямой, то её координатам ![]() соответствует вполне конкретное значение параметра, обозначим его через
соответствует вполне конкретное значение параметра, обозначим его через ![]() . Тогда координаты точки запишутся в виде:
. Тогда координаты точки запишутся в виде:
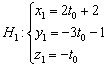
Или: ![]()
Жизнь налаживается, одна неизвестная – всё-таки не три неизвестных.
2) Такое же надругательство нужно осуществить над второй точкой. Перепишем уравнения второй прямой в параметрическом виде:
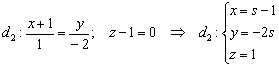
Если точка ![]() принадлежит данной прямой, то при вполне конкретном значении
принадлежит данной прямой, то при вполне конкретном значении ![]() её координаты должны удовлетворять параметрическим уравнениям:
её координаты должны удовлетворять параметрическим уравнениям:
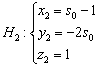
Или: ![]()
3) Вектор ![]() , как и ранее найденный вектор
, как и ранее найденный вектор ![]() , будет направляющим вектором прямой
, будет направляющим вектором прямой ![]() . Как составить вектор по двум точкам, рассматривалось в незапамятные времена на уроке Векторы для чайников. Сейчас отличие состоит в том, что координаты векторов записаны с неизвестными значениям параметров. Ну и что? Никто же не запрещает из координат конца вектора вычесть соответствующие координаты начала вектора.
. Как составить вектор по двум точкам, рассматривалось в незапамятные времена на уроке Векторы для чайников. Сейчас отличие состоит в том, что координаты векторов записаны с неизвестными значениям параметров. Ну и что? Никто же не запрещает из координат конца вектора вычесть соответствующие координаты начала вектора.
Есть две точки: ![]() .
.
Находим вектор:
![]()
4) Поскольку направляющие векторы ![]() коллинеарны, то один вектор линейно выражается через другой с некоторым коэффициентом пропорциональности «лямбда»:
коллинеарны, то один вектор линейно выражается через другой с некоторым коэффициентом пропорциональности «лямбда»:
![]()
Или покоординатно:
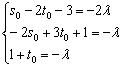
Получилась самая, что ни на есть обычная система линейных уравнений с тремя неизвестными ![]() , которая стандартно разрешима, например, методом Крамера. Но здесь так извращаться, конечно, не надо, из третьего уравнения выразим «лямбду» и подставим её в первое и второе уравнение:
, которая стандартно разрешима, например, методом Крамера. Но здесь так извращаться, конечно, не надо, из третьего уравнения выразим «лямбду» и подставим её в первое и второе уравнение:
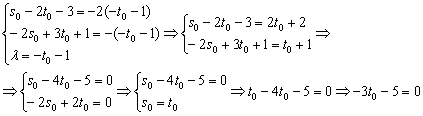
Таким образом: ![]() , а «лямбда» нам не потребуется. То, что значения параметров получились одинаковыми – чистая случайность.
, а «лямбда» нам не потребуется. То, что значения параметров получились одинаковыми – чистая случайность.
5) Небо полностью проясняется, подставим найденные значения ![]() в наши точки:
в наши точки:
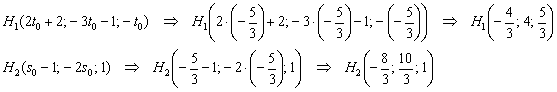
Направляющий вектор ![]() особо не нужен, так как уже найден его коллега
особо не нужен, так как уже найден его коллега ![]() .
.
После длинного пути всегда интересно выполнить проверку.
Подставим координаты точки ![]() в уравнения
в уравнения ![]() :
:
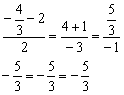
Получены верные равенства.
Подставим координаты точки ![]() в уравнения
в уравнения ![]() :
:
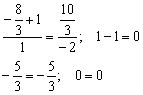
Получены верные равенства.
6) Заключительный аккорд: составим уравнения прямой ![]() по точке
по точке ![]() (можно взять
(можно взять ![]() ) и направляющему вектору
) и направляющему вектору ![]() :
:
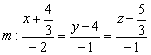
В принципе, можно подобрать «хорошую» точку с целыми координатами, но это уже косметика.
Как найти расстояние между скрещивающимися прямыми?
г) Срубаем четвёртую голову дракона.
Способ первый. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра: ![]() .
.
Крайние точки общего перпендикуляра ![]() найдены в предыдущем пункте, и задача элементарна:
найдены в предыдущем пункте, и задача элементарна:
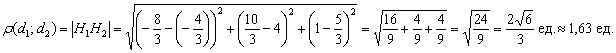
Способ второй. На практике чаще всего концы общего перпендикуляра неизвестны, поэтому используют другой подход. Через две скрещивающиеся прямые можно провести параллельные плоскости, и расстояние между данными плоскостями равно расстоянию ![]() между данными прямыми. В частности, между этими плоскостями и торчит общий перпендикуляр.
между данными прямыми. В частности, между этими плоскостями и торчит общий перпендикуляр.
В курсе аналитической геометрии из вышесказанных соображений выведена формула нахождения расстояния между скрещивающимися прямыми:
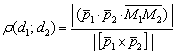 (вместо наших точек «эм один», «эм два» можно взять произвольные точки прямых).
(вместо наших точек «эм один», «эм два» можно взять произвольные точки прямых).
Смешанное произведение векторов уже найдено в пункте «а»: ![]() .
.
Векторное произведение векторов найдено в пункте «бэ»: ![]() , вычислим его длину:
, вычислим его длину: ![]()
Таким образом: ![]()
Гордо выложим трофеи в один ряд,
ответ:
а) ![]() , значит, прямые скрещиваются, что и требовалось доказать;
, значит, прямые скрещиваются, что и требовалось доказать;
б) ![]() ;
;
в) 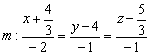 ;
;
г) ![]()
Что ещё можно рассказать про скрещивающиеся прямые? Между ними определён угол. Но универсальную формулу угла рассмотрим в следующем параграфе:
Пересекающиеся прямые в пространстве
Пересекающиеся прямые пространства обязательно лежат в одной плоскости:
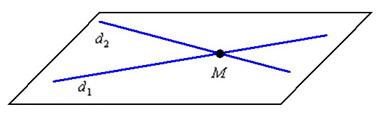
Первая мысль – всеми силами навалиться на точку пересечения ![]() . И сразу же подумалось, зачем себе отказывать в правильных желаниях?! Давайте навалимся на неё прямо сейчас!
. И сразу же подумалось, зачем себе отказывать в правильных желаниях?! Давайте навалимся на неё прямо сейчас!
Как найти точку пересечения пространственных прямых?
Пример 14
Найти точку пересечения прямых
![]()
Решение: перепишем уравнения прямых в параметрической форме:
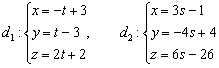
Данная задача подробно рассматривалась в Примере № 7 данного урока, а сами прямые, к слову, я взял из Примера № 12. Врать не буду, новые лень придумывать.
Приём решения стандартен и уже встречался, когда мы вымучивали уравнения общего перпендикуляра скрещивающихся прямых.
Точка пересечения прямых ![]() принадлежит прямой
принадлежит прямой ![]() , поэтому её координаты
, поэтому её координаты ![]() удовлетворяют параметрическим уравнениям данной прямой, и им соответствует вполне конкретное значение параметра
удовлетворяют параметрическим уравнениям данной прямой, и им соответствует вполне конкретное значение параметра ![]() :
:
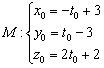
Но эта же точка принадлежит и второй прямой, следовательно:
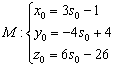
Приравниваем соответствующие уравнения и проводим упрощения:
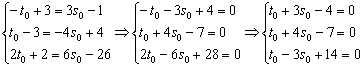
Получена система трёх линейных уравнений с двумя неизвестными. Если прямые пересекаются (что доказано в Примере № 12), то система обязательно совместна и имеет единственное решение. Её можно решить методом Гаусса, но уж таким фетишизмом грешить не будем, поступим проще: из первого уравнения выразим «тэ нулевое» и подставим его во второе и третье уравнение:
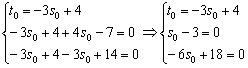
Последние два уравнения получились, по сути, одинаковыми, и из них следует, что ![]() . Тогда:
. Тогда: ![]()
Подставим найденное значение параметра ![]() в уравнения:
в уравнения:
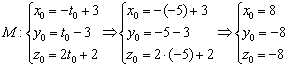
Ответ: ![]()
Для проверки подставим найденное значение параметра ![]() в уравнения:
в уравнения: 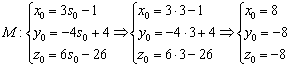
Получены те же самые координаты, что и требовалось проверить. Дотошные читатели могу подставить координаты точки ![]() и в исходные канонические уравнения прямых.
и в исходные канонические уравнения прямых.
Кстати, можно было поступить наоборот: точку ![]() найти через «эс нулевое», а проверить – через «тэ нулевое».
найти через «эс нулевое», а проверить – через «тэ нулевое».
Известная математический примета гласит: там, где обсуждают пересечение прямых, всегда пахнет перпендикулярами.
Как построить прямую пространства, перпендикулярную данной?
(прямые пересекаются)
Пример 15
а) Составить уравнения прямой, проходящей через точку ![]() перпендикулярно прямой
перпендикулярно прямой ![]() (прямые пересекаются).
(прямые пересекаются).
б) Найти расстояние от точки ![]() до прямой
до прямой ![]() .
.
Примечание: оговорка «прямые пересекаются» – существенна. Через точку ![]()
можно провести бесконечно много перпендикулярных прямых, которые будут скрещиваться с прямой «эль». Единственное решение имеет место в случае, когда через данную точку проводится прямая, перпендикулярная двум заданным прямым (см. Пример № 13, пункт «б»).
а) Решение: неизвестную прямую обозначим через ![]() . Выполним схематический чертёж:
. Выполним схематический чертёж:
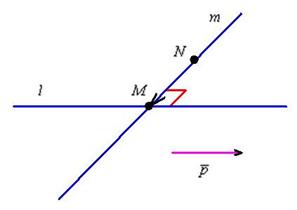
Что известно о прямой ![]() ? По условию дана точка
? По условию дана точка ![]() . Для того, чтобы составить уравнения прямой, нужно найти направляющий вектор. В качестве такого вектора вполне подойдёт вектор
. Для того, чтобы составить уравнения прямой, нужно найти направляющий вектор. В качестве такого вектора вполне подойдёт вектор ![]() , им и займемся. Точнее, возьмём за шкирку его неизвестный конец.
, им и займемся. Точнее, возьмём за шкирку его неизвестный конец.
1) Вытащим из уравнений прямой «эль» её направляющий вектор ![]() , а сами уравнения перепишем в параметрической форме:
, а сами уравнения перепишем в параметрической форме:
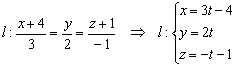
Многие догадались, сейчас уже в третий раз за урок фокусник достанет белого лебедя из шляпы. Рассмотрим точку ![]() с неизвестными координатами. Поскольку точка
с неизвестными координатами. Поскольку точка ![]() , то её координаты
, то её координаты ![]() удовлетворяют параметрическим уравнениям прямой «эль» и им соответствует конкретное значение параметра:
удовлетворяют параметрическим уравнениям прямой «эль» и им соответствует конкретное значение параметра:
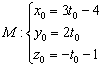
Или одной строкой: ![]()
Тогда: ![]()
2) По условию прямые должны быть перпендикулярны, следовательно, их направляющие векторы ![]() – ортогональны. А если векторы ортогональны, то их скалярное произведение равно нулю:
– ортогональны. А если векторы ортогональны, то их скалярное произведение равно нулю:
![]()
Что получилось? Простейшее линейное уравнение с одной неизвестной:
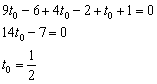
3) Значение параметра известно, найдём точку:
![]()
и направляющий вектор:
![]() .
.
4) Уравнения прямой ![]() составим по точке
составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
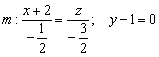
Знаменатели пропорции получились дробные, и это как раз тот случай, когда от дробей уместно избавиться. Я просто умножу их на –2:
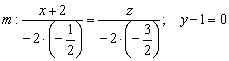
Ответ: ![]()
Примечание: более строгая концовка решения оформляется так: составим уравнения прямой по точке ![]() и направляющему вектору
и направляющему вектору ![]() . Действительно, если вектор
. Действительно, если вектор ![]() является навправляющим вектором прямой, то коллинеарный ему вектор
является навправляющим вектором прямой, то коллинеарный ему вектор ![]() , естественно, тоже будет направляющим вектором данной прямой.
, естественно, тоже будет направляющим вектором данной прямой.
Проверка состоит из двух этапов:
1) проверяем направляющие векторы прямых на ортогональность;
2) подставляем координаты точки ![]() в уравнения каждой прямой, они должны «подходить» и там и там.
в уравнения каждой прямой, они должны «подходить» и там и там.
О типовых действиях говорилось очень много, поэтому я выполнил проверку на черновике.
Кстати, запамятовал ещё пунктик – построить точку «зю» симметричную точке «эн» относительно прямой «эль». Впрочем, есть хороший «плоский аналог», с которым можно ознакомиться в статье Простейшие задачи с прямой на плоскости. Здесь же всё отличие будет в дополнительной «зетовой» координате.
Как найти расстояние от точки до прямой в пространстве?
б) Решение: найдём расстояние от точки ![]() до прямой
до прямой ![]() .
.
Способ первый. Данное расстояние в точности равно длине перпендикуляра ![]() :
: ![]() . Решение очевидно: если известны точки
. Решение очевидно: если известны точки ![]() , то:
, то:
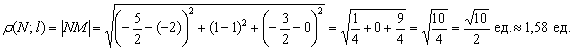
Способ второй. В практических задачах основание перпендикуляра ![]() частенько тайна за семью печатями, поэтому рациональнее пользоваться готовой формулой.
частенько тайна за семью печатями, поэтому рациональнее пользоваться готовой формулой.
Расстояние от точки ![]() до прямой
до прямой ![]() выражается формулой:
выражается формулой:
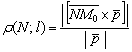 , где
, где ![]() – направляющий вектор прямой «эль», а
– направляющий вектор прямой «эль», а ![]() – произвольная точка, принадлежащая данной прямой.
– произвольная точка, принадлежащая данной прямой.
Решаем:
1) Из уравнений прямой ![]() достаём направляющий вектор
достаём направляющий вектор ![]() и самую доступную точку
и самую доступную точку ![]() .
.
2) Точка ![]() известна из условия, заточим вектор:
известна из условия, заточим вектор:
![]()
3) Найдём векторное произведение и вычислим его длину:
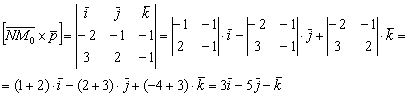
![]()
4) Рассчитаем длину направляющего вектора:
![]()
5) Таким образом, расстояние от точки до прямой:
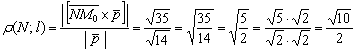
Ответ: ![]()
После разобранной задачи вам не составит труда разобраться в следующем примере:
Пример 16
В пространстве задан треугольник координатами своих вершин ![]() . Найти высоту
. Найти высоту ![]() и её длину.
и её длину.
Это пример для самостоятельного решения. Не забывайте выполнять схематические чертежи! Полное решение и ответ в конце урока.
В заключение параграфа рассмотрим угол.
Как найти угол между прямыми в пространстве?
Рисунка приводить не буду, думаю, всем понятно, что это за угол.
Понятие угла в пространстве определено не только для пересекающихся прямых, но и для скрещивающихся прямых. Угол «альфа» между двумя прямыми определяется как угол между их направляющими векторами. А формула едина и хорошо вам знакома:
![]() , где
, где ![]() – направляющие векторы двух пересекающихся либо скрещивающихся пространственных прямых.
– направляющие векторы двух пересекающихся либо скрещивающихся пространственных прямых.
В частности, если ![]() , то прямые перпендикулярны.
, то прямые перпендикулярны.
Приведённая формула может дать любой угол от 0 до 180 градусов включительно, и многие авторитетные авторы учебников по геометрии углом между пространственными прямыми называют каждый из 4 углов. Однако на практике, как и в случае угла между «плоскими» прямыми, от вас, скорее всего, потребуют острый угол (что, в общем-то, логично). Поэтому если вы получили по формуле тупой угол, например, 120 градусов, то от греха подальше, внесите дополнение, что угол между прямыми равен: 180 – 120 = 60 градусов
В примерах особого смысла нет, сильно сомневаюсь, что кто-то неправильно найдёт направляющие векторы пространственных прямых по их уравнениям. А практические задачи на применение самой формулы можно посмотреть, например, в статье Скалярное произведение векторов.
Скоро-скоро грядут задачи на плоскость и прямую в пространстве, поэтому немного освежаем материал об уравнении плоскости. В контексте параграфа полезен следующий вопрос: определяют ли две пересекающиеся прямые плоскость в пространстве? Да, конечно, если даны две пересекающиеся прямые, то они однозначно определят плоскость, в которой лежат. Уравнение данной плоскости можно составить по двум направляющим векторам и какой-нибудь точке, принадлежащей любой из прямых.
Параллельные прямые в пространстве
Параллельные прямые пространства, как и пересекающиеся прямые тоже лежат в одной плоскости:
Что сразу можно сказать? Они не пересекаются, и у них один и тот же направляющий вектор.
В начале этой статьи я зарубил четырёхглавого дракона, ловите мой меч-кладенец, вас поджидает стандартный шестиглазый зверь:
Пример 17
Дана прямая ![]() . Требуется:
. Требуется:
а) построить прямую ![]() , параллельную данной и проходящую через точку
, параллельную данной и проходящую через точку ![]()
б) будут ли параллельные прямые ![]() однозначно определять плоскость в пространстве? Если да, то составить уравнение данной плоскости;
однозначно определять плоскость в пространстве? Если да, то составить уравнение данной плоскости;
в) найти расстояние между параллельными прямыми.
Постарайтесь самостоятельно, не заглядывая в образец решения, выполнить предложенные задания.
Вот, пожалуй, и все основные задачи с пространственными прямыми. После изучения уравнения плоскости и уравнений прямой в пространстве, можно приступить к рассмотрению задач на прямую и плоскость, они вряд ли покажутся вам сложнее.
Желаю успехов!
Решения и ответы:
Пример 12. Решение:
1) Находим направляющие векторы и точки, принадлежащие данным прямым. Для нахождения точек удобно использовать нулевые значения параметров ![]() :
:
![]()
2) Найдём вектор: ![]()
3) Вычислим смешанное произведение векторов:
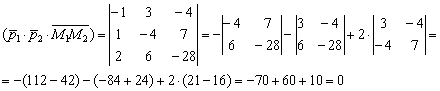
Таким образом, прямые ![]() могут пересекаться, быть параллельными или совпадать.
могут пересекаться, быть параллельными или совпадать.
4) Исследуем направляющие векторы ![]() на коллинеарность:
на коллинеарность:
![]() , следовательно, направляющие векторы не коллинеарны, и прямые пересекаются.
, следовательно, направляющие векторы не коллинеарны, и прямые пересекаются.
Ответ: ![]()
Пример 16. Решение: 1) Выполним схематический чертёж:
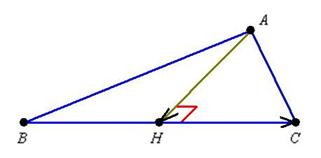
2) Найдём вектор ![]() .
.
3) Запишем параметрические уравнения прямой ![]() по точке
по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
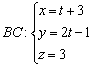
4) Точка ![]() , поэтому её координаты удовлетворяют параметрическим уравнениям данной прямой:
, поэтому её координаты удовлетворяют параметрическим уравнениям данной прямой: 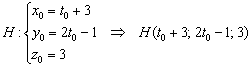 .
.
5) Найдём вектор ![]() .
.
6) Так как ![]() – высота треугольника, то
– высота треугольника, то ![]() и:
и:
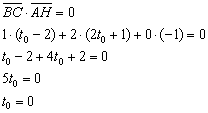
7) Найдём точку: ![]()
Точка ![]() совпала с точкой
совпала с точкой ![]() , значит, высота
, значит, высота ![]() совпадает со стороной
совпадает со стороной ![]() , и треугольник является прямоугольным.
, и треугольник является прямоугольным.
8) Найдём вектор ![]() .
.
9) Составим уравнения высоты ![]() (катета
(катета ![]() ) по точке
) по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]()
10) Найдём длину высоты ![]() как длину вектора
как длину вектора ![]() :
:
![]()
Ответ: ![]()
Пример 17. Решение:
а) Из уравнений прямой ![]() найдём её направляющий вектор:
найдём её направляющий вектор: ![]() . Уравнения прямой
. Уравнения прямой ![]() составим по точке
составим по точке ![]() и направляющему вектору
и направляющему вектору ![]() :
:
![]()
б) Да, две параллельные прямые однозначно определяют плоскость, в которой они лежат.
Точка ![]() принадлежит первой прямой.
принадлежит первой прямой.
Найдём вектор: ![]()
Уравнение искомой плоскости составим по точке ![]() и двум неколлинеарным векторам
и двум неколлинеарным векторам ![]() :
:
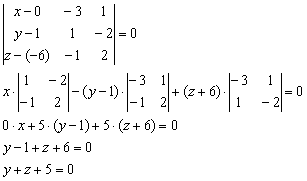
в) Расстояние между параллельными прямыми ![]() найдём как расстояние от точки до прямой:
найдём как расстояние от точки до прямой: 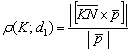 (формула из Примера № 15).
(формула из Примера № 15).
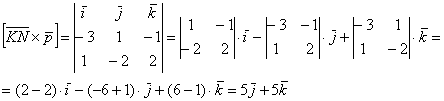
Таким образом:
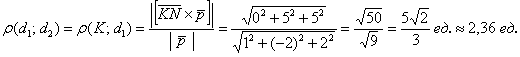
Ответ:
а) ![]()
б) да, ![]()
в) ![]()
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright