


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Задачи с линиями 2-го порядка.
Как найти геометрическое место точек?
Данный практикум представляет собой логическое продолжение лекции о линиях второго порядка и её популярных представителях – эллипсе, гиперболе и параболе. Сегодня мы закрепим пройденный материал многочисленными задачами, и, кроме того, дополним теоретический багаж знаниями, которые я намеренно скрыл на первых занятиях, чтобы не перегружать «чайников» новой информацией. Признаюсь честно, ненавижу вымучивать первые абзацы своих статей (особенно, когда готов чёткий план урока), поэтому разольём кофе по чашкам, сядем в круг и перейдём к обсуждению вопросов по существу.
В самостоятельных и контрольных работах наиболее часто встречаются следующие задания:
– Найти геометрическое место точек (или составить уравнение множества точек), каждая из которых удовлетворяет определённым аналитическим условиям. Безусловно, данная формулировка является общей и не факт, что в итоге должна получиться обязательно линия, и обязательно второго порядка. Однако в контексте рассматриваемой темы эти магические слова практически всегда вызывают к жизни уравнение эллипса, окружности, гиперболы либо параболы.
– Привести уравнение линии 2-го порядка к каноническому виду. Понятие канонического вида уравнения, а также некоторые элементы этой задачи многим читателям уже знакомы, и в ближайшем будущем вам представится отличная возможность продвинуться дальше.
Нередко оба блюда подаются за один раз, то есть сначала требуется составить уравнение линии, а затем привести его к каноническому виду + в качестве десерта найти вершины, фокусы, эксцентриситет, директрисы, выполнить чертёж и т. д. Как гостеприимный хозяин заведения постараюсь всех накормить досыта, да так – чтобы некоторые не только с трудом вышли из-за стола, но и остались здесь на ночёвку =) Начислим для аппетита:
Задача 1
Составить уравнение линии, расстояние каждой точки которой от точки ![]() в два раза больше, чем от точки
в два раза больше, чем от точки ![]() . Выполнить чертёж. Привести полученное уравнение к каноническому виду.
. Выполнить чертёж. Привести полученное уравнение к каноническому виду.
Решение данной задачи всегда начинается стандартно – в рассмотрение вводится некоторая точка ![]() с переменными координатами, которая принадлежит искомой линии.
с переменными координатами, которая принадлежит искомой линии.
Таким образом, наша аналитическая формулировка конкретизируется следующим образом: «составить уравнение линии, расстояние каждой точки ![]() которой от точки
которой от точки ![]() в два раза больше, чем от точки
в два раза больше, чем от точки ![]() ». Немного приостановимся и ответим на ключевой вопрос: о чём здесь идёт речь? Очевидно, что задач можно придумать бесконечно много, поэтому, в первую очередь необходимо правильно понять условие.
». Немного приостановимся и ответим на ключевой вопрос: о чём здесь идёт речь? Очевидно, что задач можно придумать бесконечно много, поэтому, в первую очередь необходимо правильно понять условие.
А речь здесь идёт о расстоянии ![]() от точки «а» до точки «эм» и о расстоянии
от точки «а» до точки «эм» и о расстоянии ![]() от точки «бэ» до той же точки «эм». Формула длины отрезка нам хорошо знакома ещё с первого урока по аналитической геометрии. Напоминаю: расстояние между двумя точками
от точки «бэ» до той же точки «эм». Формула длины отрезка нам хорошо знакома ещё с первого урока по аналитической геометрии. Напоминаю: расстояние между двумя точками ![]() рассчитывается по формуле
рассчитывается по формуле ![]() .
.
Запишем длины соответствующих отрезков:
для точек ![]() расстояние
расстояние ![]() ;
;
для точек ![]() расстояние
расстояние ![]() .
.
Теперь нужно составить уравнение. Согласно условию, расстояние ![]() в два раза больше расстояния
в два раза больше расстояния ![]() , следовательно, справедливо равенство:
, следовательно, справедливо равенство:
![]()
Или:
![]()
Уравнение успешно составлено, но какую линию оно задаёт – совершенно не понятно. Поэтому дальнейшие действия состоят в упрощении полученной конструкции, и сейчас мы ознакомимся с типовым техническим алгоритмом.
Во-первых, избавимся от корней. Для этого возведём в квадрат обе части:
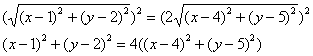
активно пользуясь формулами сокращенного умножения, раскроем все скобки:
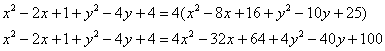
перенесём всё в левую часть и приведём подобные слагаемые:
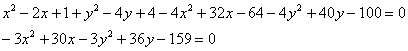
разделим каждое слагаемое на –3:
![]()
Получено уравнение линии 2-го порядка в общем виде. Уже лучше, однако, и оно как неведома зверушка. По этой причине вторая часть преобразований состоит в попытке приведения уравнения к каноническому виду. Перед нами не самый тяжёлый случай, который уже фигурировал в конце статьи о линиях второго порядка. Искусственным приёмом выделяем полные квадраты:
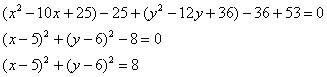
и завершающим штрихом рождаем квадрат в правой части:
![]() – уравнение окружности с центром в точке
– уравнение окружности с центром в точке ![]() радиуса
радиуса ![]() . Возьмём в руки остроногого друга:
. Возьмём в руки остроногого друга:
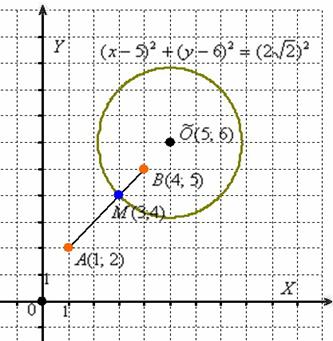
Не лишней будет кустарная, но эффективная геометрическая проверка. По условию для любой точки ![]() построенной линии расстояние
построенной линии расстояние ![]() должно быть в 2 раза больше расстояния
должно быть в 2 раза больше расстояния ![]() . Мысленно выбираем наиболее удобную точку
. Мысленно выбираем наиболее удобную точку ![]() нашей окружности и убеждаемся в справедливости данного соотношения. В целях контроля можно взять ещё какую-нибудь точку и измерить длины отрезков
нашей окружности и убеждаемся в справедливости данного соотношения. В целях контроля можно взять ещё какую-нибудь точку и измерить длины отрезков ![]() обычной линейкой.
обычной линейкой.
Заключительная часть задания состоит в приведении уравнения линии к каноническому виду. Центр канонической окружности должен располагаться в начале координат, и, как я неоднократно оговаривался, есть два способа разрулить ситуацию.
Первый, более простой метод:
1) Приведём уравнение окружности к каноническому виду путём её параллельного переноса центром в начало координат: ![]()
Второй, более солидный и правильный метод:
2) Осуществим параллельный перенос прямоугольной системы координат началом в точку ![]() :
:
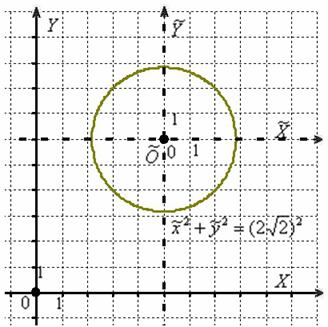
Иными словами, мы перешли к новой системе координат ![]() ТАК, чтобы уравнение нашей окружности записалось в ней каноническим образом:
ТАК, чтобы уравнение нашей окружности записалось в ней каноническим образом: ![]() .
.
На первый взгляд кажется нелепым менять систему координат из-за одной-единственной линии, но на самом деле этот подход более корректен, и об одной простой причине его корректности я расскажу на уроке Приведение уравнения линии 2-го порядка к каноническому виду.
Ответ: искомая линия ![]() представляет собой окружность с центром в точке
представляет собой окружность с центром в точке ![]() радиуса
радиуса ![]() . Каноническое уравнение:
. Каноническое уравнение: ![]() (либо
(либо ![]() в зависимости от способа приведения).
в зависимости от способа приведения).
Аналогичный пример для самостоятельного решения:
Задача 2
Составить уравнение множества точек, для каждой из которых сумма квадратов расстояний от точек ![]() равна 20. Определить тип линии, выполнить чертёж и привести уравнение к каноническому виду. Указать координаты фокусов, записать уравнение асимптот, если они есть. Вычислить эксцентриситет кривой.
равна 20. Определить тип линии, выполнить чертёж и привести уравнение к каноническому виду. Указать координаты фокусов, записать уравнение асимптот, если они есть. Вычислить эксцентриситет кривой.
Краткое оформление и чертёж в конце урока.
Систематизируем порядок решения данной задачи:
На первом шаге нужно рассмотреть точку ![]() с неизвестными координатами, которая принадлежит искомому множеству точек, и разобраться в условии задачи. Как правило, в нём говорится о расстояниях от точки «эм» до других точек и/или других линий, а также о соотношениях этих длин.
с неизвестными координатами, которая принадлежит искомому множеству точек, и разобраться в условии задачи. Как правило, в нём говорится о расстояниях от точки «эм» до других точек и/или других линий, а также о соотношениях этих длин.
На втором шаге следует найти длины нужных отрезков и в соответствии с аналитическим условием задачи составить уравнение.
На третьем шаге осуществляем упрощение полученного уравнения. Сначала приводим его к общему виду, а затем к форме, которая близкА к канонической. В некоторых задачах сразу получается каноническое уравнение.
На четвёртом шаге – чертёж.
На пятом – приведение к каноническому виду.
На шестом – фокусы, асимптоты, эксцентриситет. Напоминаю, что находить их гораздо удобнее именно из канонической записи.
На практике чаще всего заданий меньше, так, в некоторых случаях не надо приводить уравнение к каноническому виду, а в самой компактной версии не требуется и чертёжа – достаточно лишь упростить уравнение и назвать линию. Я специально «нагружаю» условия задач, чтобы образцы решений годились «на все случаи жизни». Но, тем не менее, надрываться тоже не будем, и разогреемся парой новых коктейлей:
Задача 3
Составить уравнение множества точек, для каждой из которых квадрат расстояния до точки ![]() на 16 больше квадрата расстояния до оси ординат.
на 16 больше квадрата расстояния до оси ординат.
Решение: пусть точка ![]() принадлежит искомому множеству. Тогда:
принадлежит искомому множеству. Тогда:
![]()
Примечание: строго говоря, в соответствии с формулировкой условия нужно рассмотреть ![]() (та же самая длина), но в этой и других задачах мы пренебрежём данной логической неточностью.
(та же самая длина), но в этой и других задачах мы пренебрежём данной логической неточностью.
Чему равно расстояние от точки ![]() до оси ординат? Можно воспользоваться стандартной формулой расстояния от точки до прямой, но если немного подключить воображение, то легко понять, что расстояние от любой точки до оси
до оси ординат? Можно воспользоваться стандартной формулой расстояния от точки до прямой, но если немного подключить воображение, то легко понять, что расстояние от любой точки до оси ![]() равно модулю её «иксовой» координаты:
равно модулю её «иксовой» координаты:
![]()
По условию ![]() на 16 больше, чем
на 16 больше, чем ![]() , следовательно, справедливо следующее равенство:
, следовательно, справедливо следующее равенство:
![]()
(либо ![]() )
)
Таким образом:
![]()
Раскручиваем гайки:
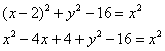
«Иксы в квадрате» взаимоуничтожаются, и, очевидно, уравнение нужно максимально приблизить к каноническому виду ![]() :
:
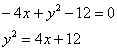
![]() – парабола с вершиной в точке
– парабола с вершиной в точке ![]() , фокальным параметром
, фокальным параметром ![]() .
.
Ответ: искомое множество точек представляет собой параболу ![]()
Если дополнительно требуется привести уравнение линии к каноническому виду, то в данном примере это осуществляется элементарно:
1) Приведём уравнение параболы к каноническому виду путём её параллельного переноса центром в начало координат: ![]()
2) Перейдём к новой прямоугольной системе координат ![]() с центром в точке
с центром в точке ![]() , тогда уравнение параболы примет вид:
, тогда уравнение параболы примет вид: ![]() .
.
Чертёж приводить не буду, поскольку параболу ![]() мы уже вертели, как хотели.
мы уже вертели, как хотели.
Задача 4
Составить уравнение множества точек, для каждой из которых расстояние до точки ![]() равно расстоянию до оси абсцисс. Выполнить чертёж. Привести уравнение к каноническому виду.
равно расстоянию до оси абсцисс. Выполнить чертёж. Привести уравнение к каноническому виду.
В образце решения последний пункт реализован обоими способами.
Разобранные задачи с окружностями (особенно часто), параболами встречаются и в школьной программе. Ну а на нашей тусовке 18+ становится всё жарче – снимайте джемперы и пиджаки:
Задача 5
Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки ![]() к расстоянию до прямой
к расстоянию до прямой ![]() постоянно и равно
постоянно и равно ![]() . Сделать чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы (если они существуют).
. Сделать чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы (если они существуют).
Решение: пусть точка ![]() принадлежит искомому множеству точек. В задаче говорится о расстоянии:
принадлежит искомому множеству точек. В задаче говорится о расстоянии:
![]() ,
,
а также о расстоянии от точки до прямой, которое вычисляется по формуле ![]() , где
, где![]() – соответствующие коэффициенты общего уравнения прямой «дэ»,
– соответствующие коэффициенты общего уравнения прямой «дэ», ![]() – координаты точки «эм».
– координаты точки «эм».
В данном случае:
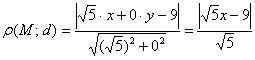 .
.
По условию для каждой точки ![]() отношение расстояния
отношение расстояния ![]() к расстоянию
к расстоянию ![]() должно быть равно
должно быть равно ![]() . А что такое отношение? Отношение – это пропорция, или попросту дробь:
. А что такое отношение? Отношение – это пропорция, или попросту дробь:
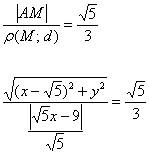
Уравнение составлено, но его вид оставляет желать лучшего. Сначала избавимся от трёхэтажной дроби. Для этого знаменатель левой части (дробь) перекинем направо:
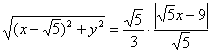
Сократим на ![]() :
:
![]()
Чтобы окончательно избавиться от дробей, «поднимем тройку» на левый берег:
![]()
Дальнейшие упрощения приобретают знакомые очертания. Возводим обе части в квадрат и раскрываем скобки:
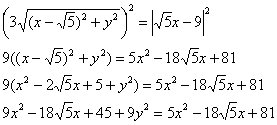
Перенесём всё налево и причешем слагаемые:
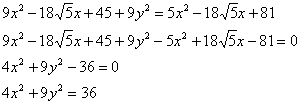
Читатели с хорошим и высоким уровнем подготовки, разумеется, могут немного видоизменять вычисления и сокращать запись, выполняя некоторые действия в уме.
Разделим обе части на 36:
![]()
Организуем трёхэтажные дроби:
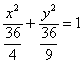
И выполним деление:
![]()
Почему целесообразен именно такой алгоритм, подробно закомментировано в Примере 4 статьи о гиперболе и параболе.
В результате:
![]() – эллипс с центром в начале координат, полуосями
– эллипс с центром в начале координат, полуосями ![]() .
.
Обратите внимание, что такая формулировка однозначно определяет эллипс и добавлять что-либо излишне.
Изобразим на чертеже найденный эллипс, точку ![]() и прямую
и прямую ![]() :
:
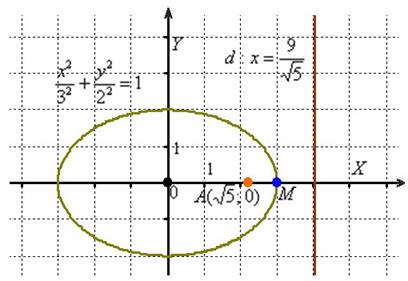
Геометрическая проверка тут затруднена, но с другой стороны и не сверхъестественна. Возьмём какую-нибудь точку эллипса, проще всего рассмотреть ![]() .
.
Для неё: ![]() .
.
По условию отношение ![]() должно равняться
должно равняться ![]() .
.
Проверяем: 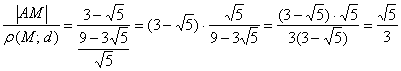 , что и требовалось проверить.
, что и требовалось проверить.
На практике можно выбрать любую точку эллипса, измерить расстояния линейкой, разделить ![]() на
на ![]() с помощью калькулятора и удостовериться, что получилось примерно
с помощью калькулятора и удостовериться, что получилось примерно ![]() .
.
В данной задаче уравнение линии нарисовалось сразу в каноническом виде, что облегчает решение. Осталось разобраться с фокусами, эксцентриситетом, асимптотами и директрисами.
Очевидно, что у эллипса отсутствуют асимптоты.
Вычислим ![]() и запишем фокусы эллипса:
и запишем фокусы эллипса:
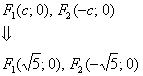 .
.
Первый фокус совпал с точкой ![]() .
.
Найдём эксцентриситет: ![]() . По ещё одному странному совпадению эксцентриситет оказался равен отношению
. По ещё одному странному совпадению эксцентриситет оказался равен отношению ![]() .
.
…однако, совпадения ли это?
Директрисы эллипса
Директриса, как вы помните из материалов о параболе, – это прямая. Причём прямая с армией горячих поклонников :D ...ну что же, шалуны, завидуйте, у эллипса их две!
Эллипс имеет две директрисы, и в каноническом положении ![]() они задаются уравнениями
они задаются уравнениями ![]() , где «эпсилон» – эксцентриситет данного эллипса.
, где «эпсилон» – эксцентриситет данного эллипса.
Для нашего героя ![]() :
:
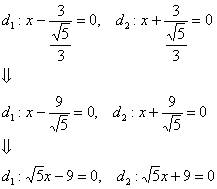
Так и есть, первая директриса полностью совпала с прямой «дэ». Более того, в условии задачи фактически сформулирована следующая теорема аналитической геометрии:
Эллипс – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от неё до соответствующей (ближайшей) директрисы равно эксцентриситету:
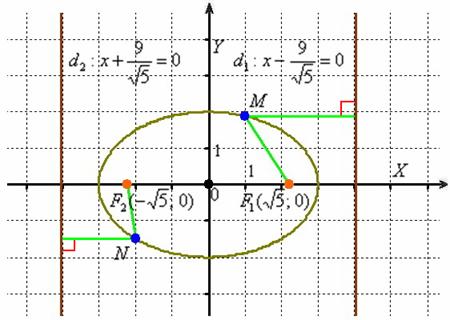
То есть для любой точки ![]() эллипса отношение её расстояния от фокуса
эллипса отношение её расстояния от фокуса ![]() к расстоянию от неё же до ближайшей директрисы
к расстоянию от неё же до ближайшей директрисы ![]() в точности равно эксцентриситету:
в точности равно эксцентриситету: ![]() .
.
Со вторым фокусом и второй директрисой аналогичная история, какую бы точку ![]() эллипса мы ни взяли – будет справедливо отношение:
эллипса мы ни взяли – будет справедливо отношение: ![]()
Ответ: искомое геометрическое место точек представляет собой эллипс ![]() с фокусами
с фокусами ![]() и эксцентриситетом
и эксцентриситетом ![]() . Уравнения директрис:
. Уравнения директрис: ![]() .
.
Похожий пример для самостоятельного решения:
Задача 6
Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки ![]() к расстоянию до прямой
к расстоянию до прямой ![]() постоянно и равно
постоянно и равно ![]() . Выполнить чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы, если они существуют.
. Выполнить чертеж. Привести уравнение линии к каноническому виду, найти фокусы, эксцентриситет, асимптоты и директрисы, если они существуют.
В образце решения концовка реализована обоими способами, выбирайте версию, которая более уместна в вашем курсе высшей математики.
Наша вечеринка в самом разгаре, и вокруг происходит столько интересного, что, порой, и говорить об этом неловко =) Зажигаем дальше!
Задача 7
Составить уравнение линии, для каждой точки которой разность расстояний до точек ![]() и
и ![]() по модулю равна 8. Привести уравнение к каноническому виду и выполнить чертёж. Найти асимптоты, фокусы, эксцентриситет и директрисы, если они существуют.
по модулю равна 8. Привести уравнение к каноническому виду и выполнить чертёж. Найти асимптоты, фокусы, эксцентриситет и директрисы, если они существуют.
Решение: пусть точка ![]() принадлежит искомой линии. Тогда:
принадлежит искомой линии. Тогда:
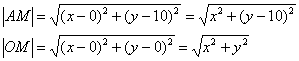
По условию:
![]()
Или:
![]()
Кстати, ничего не напоминает? Внимательные читатели уже определили линию ;-)
Корни? Модуль? Застрелитесь! Ерунда!
От модуля избавляемся немедленно:
![]()
Теперь нужно избавиться от радикалов. Возводить в квадрат сразу – идея плохая (можете попробовать), поэтому разведём корни по углам ринга:
![]()
Ну вот, теперь совсем другое дело:
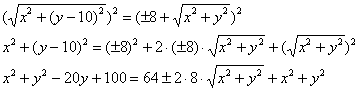
Успехи есть, но один корень остался. Оставим нашего зловреда в одиночестве и максимально упростим левую часть уравнения:
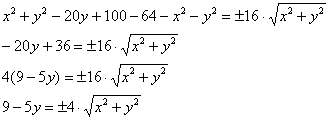
Возводим в квадрат обе части ещё раз, и заметьте, как попутно и совершенно спокойно исчезает знак «+–»:
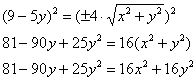
Перебросим всё направо и «развернём» уравнение:
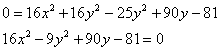
Получено уравнение линии 2-го порядка в общем виде. Выделяем полный квадрат при переменной «игрек», для этого вынесем «минус девять» за скобку:
![]()
Далее внутри скобки искусственно добавляем +25 (в целях применения формулы![]() на следующем шаге) и, чтобы уравнение не изменилось, за скобками нужно прибавить
на следующем шаге) и, чтобы уравнение не изменилось, за скобками нужно прибавить ![]() :
:
![]()
Хорошо осмыслите выполненное действие – фишка распространённая.
Собираем квадрат разности и допиливаем константы:
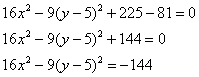
Вот тебе и раз. По всем признакам мыльная опера должна была закончиться гиперболой ![]() , но у нас «лишний» минус. Выполним проверку и раскроем скобки (что желательно сделать в любом случае)… нет, всё верно – получается исходное общее уравнение
, но у нас «лишний» минус. Выполним проверку и раскроем скобки (что желательно сделать в любом случае)… нет, всё верно – получается исходное общее уравнение ![]() .
.
Изменим знаки у обеих частей:
![]()
Уже ближе к правде, но «минус» оказался «не на своём месте». В главе о повороте и параллельном переносе гиперболы я рассказывал, что это признак поворота данной кривой на 90 градусов относительно своего канонического положения.
Но давайте сначала доведём до ума уравнение. Делим обе части на 144:
![]()
И завершающий тонкий тюнинг:
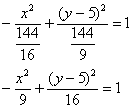
![]() – вот она, долгожданная гипербола, удовлетворяющая условию задачи, ...которое фактически представляет собой определение гиперболы =)
– вот она, долгожданная гипербола, удовлетворяющая условию задачи, ...которое фактически представляет собой определение гиперболы =)
По условию требуется сначала привести уравнение к каноническому виду, и только потом выполнить чертёж. Дабы не превысить точку кипения серого вещества, применим упрощенную схему. Однако случай всё равно не самый простой. Центр симметрии нашей подопечной находится в точке ![]() , и, кроме того, она повёрнута на 90 градусов вокруг этой точки
, и, кроме того, она повёрнута на 90 градусов вокруг этой точки
На первом шаге осуществим параллельный перенос гиперболы ![]() ТАК – чтобы её центр оказался в начале координат. В результате получится уравнение:
ТАК – чтобы её центр оказался в начале координат. В результате получится уравнение: ![]() .
.
Вторым действием повернём гиперболу вокруг начала координат на 90 градусов, при этом меняем местами значения полуосей и перебрасываем «минус» к переменной «игрек»:
![]()
В принципе, операции перестановочны, т. е. сначала можно было повернуть вокруг точки ![]() , а потом перенести центр в начало координат. Но тут промежуточное уравнение (после поворота) будет другим:
, а потом перенести центр в начало координат. Но тут промежуточное уравнение (после поворота) будет другим: ![]()
Не забывая про асимптоты ![]() , выполним чертёж:
, выполним чертёж:
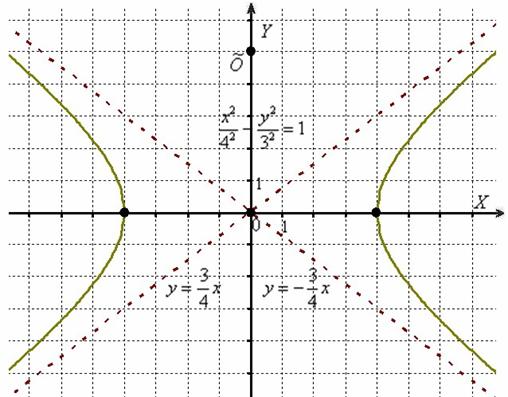
Еще раз: где изначально расположена гипербола? В точке ![]() (центр симметрии), ветви направлены вверх и вниз. И если по условию вам требуется построить график
(центр симметрии), ветви направлены вверх и вниз. И если по условию вам требуется построить график ![]() , то руководствуйтесь алгоритмом, разобранным в начале урока Гипербола и парабола.
, то руководствуйтесь алгоритмом, разобранным в начале урока Гипербола и парабола.
Но работать гораздо удобнее с приведённым уравнением. Найдём фокусы:
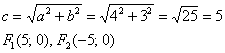
В случае перечисленных выше преобразований они как раз и «переезжают» в точки ![]() условия задачи.
условия задачи.
Вычислим эксцентриситет: ![]()
Директрисы гиперболы
У гиперболы, точно так же, как у эллипса, две директрисы. В каноническом случае ![]() они расположены между ветвями гиперболы и задаются такими же уравнениями
они расположены между ветвями гиперболы и задаются такими же уравнениями ![]() , где «эпсилон» эксцентриситет данной гиперболы.
, где «эпсилон» эксцентриситет данной гиперболы.
В рассматриваемом примере:
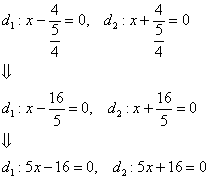
Более того, для гиперболы справедлива абсолютно такая же теорема:
Гипербола – есть множество всех точек плоскости, таких, что отношение расстояния до каждой точки от фокуса к расстоянию от неё до соответствующей (ближайшей) директрисы равно эксцентриситету:
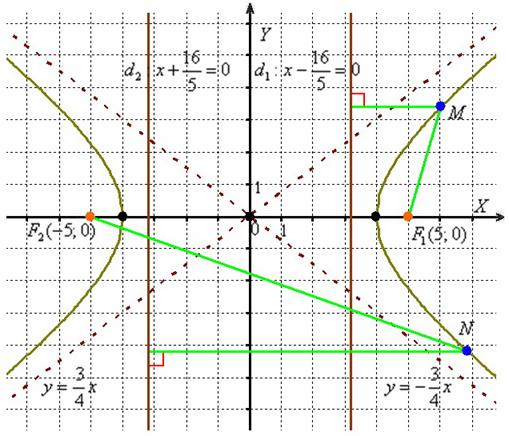
То есть для любой точки ![]() гиперболы отношение её расстояния от фокуса
гиперболы отношение её расстояния от фокуса ![]() к расстоянию от неё же до ближайшей директрисы
к расстоянию от неё же до ближайшей директрисы ![]() равно эксцентриситету:
равно эксцентриситету: ![]() .
.
Для пары ![]() и любой точки
и любой точки ![]() гиперболы (ради разнообразия я выбрал демонстрационную точку дальней ветви) отношение такое же:
гиперболы (ради разнообразия я выбрал демонстрационную точку дальней ветви) отношение такое же: ![]()
К слову, у параболы с её единственным фокусом и единственной директрисой по определению эти длины относятся «один к одному», поэтому эксцентриситет любой параболы и равен единице.
Ответ: искомая линия представляет собой гиперболу ![]() с центром симметрии в точке
с центром симметрии в точке ![]() и повёрнутую на 90 градусов относительно своего канонического положения. Канонический вид уравнения:
и повёрнутую на 90 градусов относительно своего канонического положения. Канонический вид уравнения: ![]() , фокусы:
, фокусы: ![]() , эксцентриситет:
, эксцентриситет: ![]() , асимптоты:
, асимптоты: ![]() , директрисы:
, директрисы: ![]() .
.
Очень хотелось упростить пример, но он взят из конкретной работы, поэтому пришлось с упорным занудством разобрать все-все-все тонкости и технические приёмы. Налью всем по стакану молока за вредность и подкину задание для самостоятельного решения:
Задача 8
Найти уравнение геометрического места точек, для каждой из которых отношение расстояния до точки ![]() к расстоянию до прямой
к расстоянию до прямой ![]() постоянно и равно
постоянно и равно ![]() . Сделать точный чертеж.
. Сделать точный чертеж.
Подумайте, о какой это точке и о какой прямой шепчет условие ;-)
Героически разбираемся с решением и чертежом, после чего с чистой душой и лёгким сердцем засыпаем на раскладушках возле мониторов, чтобы проснуться к следующему занятию со свежими головами и розовыми лицами.
Спокойной ночи!
Решения и ответы:
Пример 2. Решение: пусть точка ![]() принадлежит искомому множеству точек. Тогда:
принадлежит искомому множеству точек. Тогда:
![]()
![]()
По условию:
![]()
Или:
![]()
Упростим уравнение:
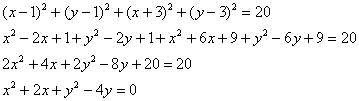
Выделим полные квадраты:
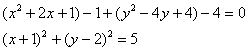
![]() – окружность с центром в точке
– окружность с центром в точке ![]() радиуса
радиуса ![]()
Выполним чертеж:
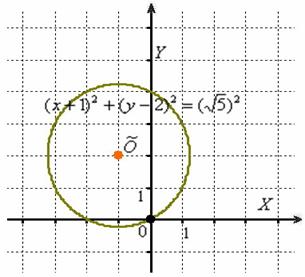
Приведём уравнение к каноническому виду.
1) Способ первый. Осуществим параллельный перенос окружности центром в начало координат: ![]() .
.
2) Способ второй. С помощью параллельного переноса перейдём от исходной к новой прямоугольной системе координат ![]() с началом в точке
с началом в точке ![]() . Таким образом, уравнение окружности запишется в каноническом виде:
. Таким образом, уравнение окружности запишется в каноническом виде: ![]() .
.
Ответ: уравнение искомого множества точек ![]() задаёт окружность с центром в точке
задаёт окружность с центром в точке ![]() радиуса
радиуса ![]() . Канонический вид уравнения:
. Канонический вид уравнения: ![]() (или
(или ![]() в зависимости от способа). Фокусы окружности совпадают и находятся в её центре. У окружности отсутствуют асимптоты. Эксцентриситет любой окружности равен нулю.
в зависимости от способа). Фокусы окружности совпадают и находятся в её центре. У окружности отсутствуют асимптоты. Эксцентриситет любой окружности равен нулю.
Пример 4. Решение: пусть точка ![]() принадлежит искомому множеству точек. Тогда:
принадлежит искомому множеству точек. Тогда:
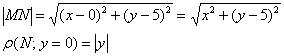
По условию:
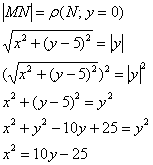
![]() – парабола, ветви которой направлены вверх, с вершиной
– парабола, ветви которой направлены вверх, с вершиной ![]() и фокальным параметром
и фокальным параметром ![]() :
:
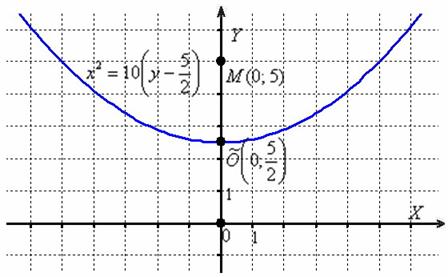
Примечание: аналитическое условие задачи формулирует определение данной параболы, т. е. точка ![]() является её фокусом, а ось абсцисс – директрисой.
является её фокусом, а ось абсцисс – директрисой.
Приведём уравнение кривой к каноническому виду:
1) Осуществим параллельный перенос параболы ![]() вершиной в начало координат:
вершиной в начало координат: ![]() и повернём её на 90 градусов по часовой стрелке:
и повернём её на 90 градусов по часовой стрелке: ![]() .
.
Либо так: повернём параболу ![]() по часовой стрелке на 90 градусов относительно точки
по часовой стрелке на 90 градусов относительно точки ![]() :
: ![]() и перенесём её в начало координат:
и перенесём её в начало координат: ![]() .
.
2) Повернём прямоугольную систему координат ![]() на 90 градусов против часовой стрелки и перенесём её началом координат в точку
на 90 градусов против часовой стрелки и перенесём её началом координат в точку ![]() . Тогда в новой системе координат
. Тогда в новой системе координат ![]() уравнение данной параболы примет канонический вид
уравнение данной параболы примет канонический вид ![]() .
.
Ответ: ![]() – парабола. Каноническое уравнение:
– парабола. Каноническое уравнение: ![]() (либо
(либо ![]() в зависимости от способа приведения).
в зависимости от способа приведения).
Пример 6. Решение: пусть точка ![]() принадлежит искомому множеству точек. Тогда:
принадлежит искомому множеству точек. Тогда:
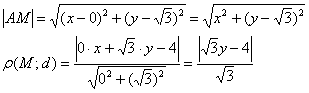
По условию:
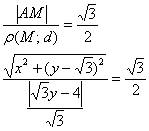
Приведем уравнение к каноническому виду:
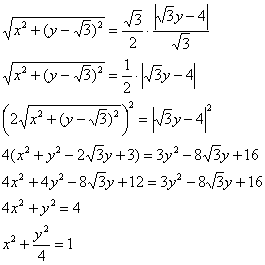
![]() – эллипс с центром в начале координат и полуосями, равными 1 и 2.
– эллипс с центром в начале координат и полуосями, равными 1 и 2.
Примечание: здесь нежелательна формулировка «с полуосями ![]() », поскольку буквой «а» стандартно обозначают большую полуось, а «единица» таковой не является по причине неканонического положения эллипса.
», поскольку буквой «а» стандартно обозначают большую полуось, а «единица» таковой не является по причине неканонического положения эллипса.
Выполним чертеж:
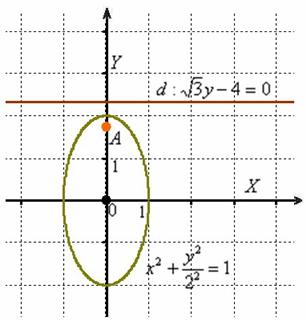
Приведём уравнение к каноническому виду:
1) Способ первый. Повернём эллипс вокруг центра на 90 градусов: ![]() .
.
Вычислим ![]() и запишем фокусы:
и запишем фокусы:
![]() .
.
Найдём эксцентриситет: ![]() .
.
Директрисы эллипса задаются уравнениями ![]() , в данном случае:
, в данном случае:
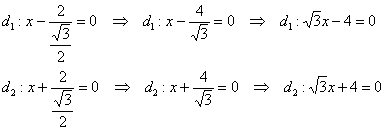
Ответ: искомое множество точек представляет собой эллипс ![]() . Канонический вид уравнения:
. Канонический вид уравнения: ![]() . Фокусы:
. Фокусы: ![]() , эксцентриситет:
, эксцентриситет: ![]() , директрисы:
, директрисы: ![]() .
.
2) Способ второй. Используем поворот координатных осей на 90 градусов против часовой стрелки, то есть перейдём к новой системе координат ![]() (ось
(ось ![]() совпадёт с осью
совпадёт с осью ![]() старой системы координат, а ось
старой системы координат, а ось ![]() будет противоположно направлена к оси
будет противоположно направлена к оси ![]() ). Тогда:
). Тогда: ![]() .
.
! Все дальнейшие действия проводятся в новой системе координат – с переменными ![]() !
!
Вычислим ![]() и запишем фокусы эллипса:
и запишем фокусы эллипса:
![]() .
.
Эксцентриситет: ![]() .
.
Директрисы эллипса задаются уравнениями ![]() , в данном случае:
, в данном случае:
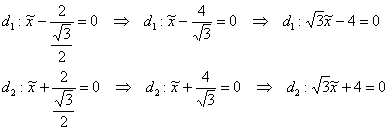
Ответ: искомое множество точек представляет собой эллипс ![]() . Канонический вид уравнения:
. Канонический вид уравнения: ![]() . Фокусы:
. Фокусы: ![]() , эксцентриситет:
, эксцентриситет: ![]() , директрисы:
, директрисы: ![]() .
.
Пример 8. Решение: пусть точка ![]() принадлежит искомому множеству точек. Тогда:
принадлежит искомому множеству точек. Тогда:
![]() ,
,
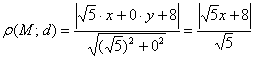 .
.
По условию:
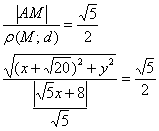
Упростим уравнение:
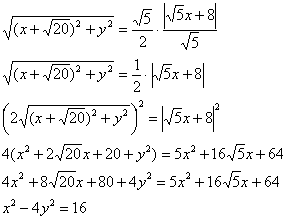
![]() – каноническое уравнение гиперболы с действительной полуосью
– каноническое уравнение гиперболы с действительной полуосью ![]() , мнимой полуосью
, мнимой полуосью ![]() .
.
Выполним чертёж:
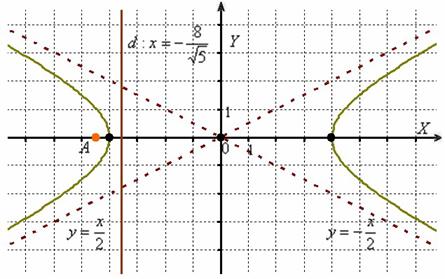
Ответ: ![]()
Примечание: точка ![]() является вторым фокусом гиперболы, прямая
является вторым фокусом гиперболы, прямая ![]() – второй директрисой, а их отношение
– второй директрисой, а их отношение ![]() – эксцентриситетом.
– эксцентриситетом.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright