Высшая математика – просто и доступно!

Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net

Наш форум, библиотека и блог: mathprofi.com

Высшая математика:

Математика для заочников

Математические формулы,
таблицы и другие материалы

Книги по математике

Математические сайты

+-*/^ Удобный калькулятор

+ «Дробовик»   

Учимся решать:

  Карта сайта

Не нашлось нужной задачи?
Сборники готовых решений!

Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi

Обратная связь:

Часто задаваемые вопросы
Гостевая книга Отблагодарить автора >>>

Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом

Карта сайта

---

Производная сложной функции. Примеры решений

На данном уроке мы научимся находить производную сложной функции. Урок является логическим продолжением занятия Как найти производную?, на котором мы разобрали простейшие производные, а также познакомились с правилами дифференцирования и некоторыми техническими приемами нахождения производных. Таким образом, если с производными функций у Вас не очень или какие-нибудь моменты данной статьи будут не совсем понятны, то сначала ознакомьтесь с вышеуказанным уроком. Пожалуйста, настройтесь на серьезный лад – материал не из простых, но я все-таки постараюсь  изложить его просто и доступно.

На практике с производной сложной функции приходится сталкиваться очень часто, я бы даже сказал, почти всегда, когда Вам даны задания на нахождение производных.

Смотрим в справку на правило (№ 5) дифференцирования сложной функции:

Разбираемся. Прежде всего, обратим внимание на запись . Здесь у нас две функции –  и , причем функция , образно говоря, вложена в функцию . Функция такого вида (когда одна функция вложена в другую) и называется сложной функцией.

Функцию  я буду называть внешней функцией, а функцию  – внутренней (или вложенной) функцией.

! Эти определения не являются теоретическими и не должны фигурировать в чистовом оформлении заданий. Я применяю неформальные выражения «внешняя» функция, «внутренняя» функция только для того, чтобы Вам легче было понять материал.

Для того, чтобы прояснить ситуацию, рассмотрим:

Пример 1

Найти производную функции

Под синусом у нас находится не просто буква «икс», а целое выражение , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:

В данном примере уже из моих объяснений интуитивно понятно, что функция  – это сложная функция, причем двучлен  является внутренней функцией (вложением), а  – внешней функцией.

Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.

В случае простых примеров вроде  понятно, что под синус вложен двучлен. Но как быть, если всё не так очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.

Представим, что нам нужно вычислить на калькуляторе значение выражения  при  (вместо единицы может быть другое число).

Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: , поэтому двучлен  и будет внутренней функцией :
 
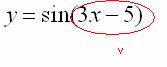
Во вторую очередь нужно будет найти , поэтому синус – будет внешней функцией:

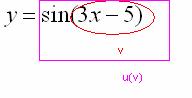
После того, как  мы РАЗОБРАЛИСЬ с внутренней и внешней функциями, самое время применить правило дифференцирования сложной функции .

Начинаем решать. Из урока Как найти производную? мы помним, что оформление решения любой производной всегда начинается так – заключаем всю функцию в скобки и ставим справа вверху штрих:

Сначала находим производную внешней функции  (синуса), смотрим в таблицу производных элементарных функций и замечаем, что . Все табличные шаблоны применимы и в том случае, если «икс» заменить любой дифференцируемой функцией . В данном примере ВМЕСТО «икс» у нас :

Обратите внимание, что внутренняя функция  не изменилась, её мы не трогаем.

Ну и совершенно понятно, что

Результат применения формулы  в чистовом оформлении выглядит так:

Далее мы берем производную внутренней функции, она очень простая:

Постоянный множитель обычно выносят в начало выражения:

Готово

Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.

Пример 2

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Пример 3

Найти производную функции

Как всегда записываем:

Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения  при . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: , значит, двучлен  – и есть внутренняя функция:

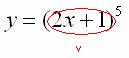
И, только потом выполняется возведение в степень , следовательно, степенная функция – это внешняя функция:

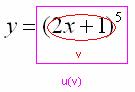
Согласно формуле , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: . Повторяем еще раз: любой табличный шаблон справедлив не только для «икс», но и для любой дифференцируемой функции . Таким образом, результат применения правила дифференцирования сложной функции   следующий:

Снова подчеркиваю, что когда мы берем производную от внешней функции , внутренняя функция  у нас не меняется:

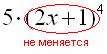
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:

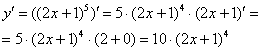
Готово.

Пример 4

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Для закрепления понимания производной сложной функции приведу пример без комментариев, попробуйте самостоятельно разобраться, порассуждать, где внешняя и где внутренняя функция, почему задания решены именно так?

Пример 5

а) Найти производную функции

б) Найти производную функции

Пример 6

Найти производную функции

Здесь у нас корень, а для того, чтобы продифференцировать корень, его удобно представить в виде степени  (вместо «икс», понятно, может быть сложное выражение). Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:

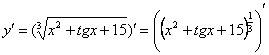
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции :

Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:

Готово. Можно ещё в скобках привести выражение к общему знаменателю и записать всё одной дробью. Красиво, конечно, но когда получаются громоздкие длинные производные – лучше этого не делать (легко запутаться, допустить ненужную ошибку, да и преподавателю будет неудобно проверять).

Пример 7

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Интересно отметить, что иногда вместо правила дифференцирования сложной функции можно использовать правило дифференцирования частного 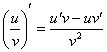, но такое решение будет выглядеть как извращение необычно. Вот характерный пример:

Пример 8

Найти производную функции

Здесь можно использовать правило дифференцирования частного 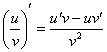, но гораздо выгоднее найти производную через правило дифференцирования сложной функции:

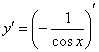
Подготавливаем функцию для дифференцирования – выносим минус за знак производной, а косинус поднимаем в числитель:

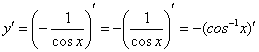
Косинус – внутренняя функция, возведение в степень – внешняя функция.
Используем наше правило :

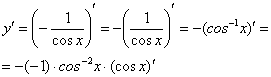
Находим производную внутренней функции, косинус сбрасываем обратно вниз:

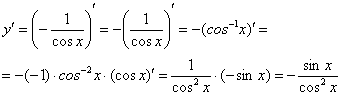
Готово. В рассмотренном примере важно не запутаться в знаках. Кстати, попробуйте решить его с помощью правила 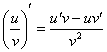, ответы должны совпасть.

Пример 9

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

До сих пор мы рассматривали случаи, когда у нас в сложной функции было только одно вложение. В практических же заданиях часто можно встретить производные, где, как матрёшки, одна в другую, вложены сразу 3, а то и 4-5 функций; правда, «матрёшки» эти с разной «росписью»:

Пример 10

Найти производную функции

Разбираемся во вложениях этой функции. Пробуем вычислить выражение  с помощью подопытного значения . Как бы мы считали на калькуляторе?

Сначала нужно найти , значит, арксинус – самое глубокое вложение:

Затем этот арксинус единицы следует возвести в квадрат :

И, наконец, семерку возводим в степень :


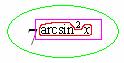
То есть в данном примере у нас три разные функции и два вложения, при этом, самой внутренней функцией является арксинус, а самой внешней функцией – показательная функция.

Начинаем решать

Согласно правилу , сначала нужно взять производную от внешней функции. Смотрим в таблицу производных и находим производную показательной функции: . Только вот ВМЕСТО «икс» у нас функция  , и мы действуем по шаблону. Итак, результат применения правила дифференцирования сложной функции   следующий:

Под штрихом у нас снова сложная функция! Но она уже проще. Легко убедиться, что внутренняя функция – арксинус, внешняя функция – степень. Согласно правилу дифференцирования сложной функции, сначала нужно взять производную от степени:

Теперь всё просто, находим по таблице производную арксинуса и немного «причесываем» результат:

Готово.

Пример 11

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

На практике правило дифференцирования сложной функции часто применяется в комбинации с остальными правилами дифференцирования.

Пример 12

Найти производную функции

Здесь у нас два больших слагаемых и сначала мы-таки используем правило дифференцирования суммы , заодно в первом слагаемом выносим постоянный множитель за знак производной по правилу :

В обоих слагаемых под штрихами у нас находится произведение функций, следовательно, нужно дважды применить правило :

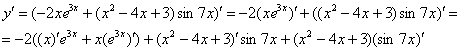
Замечаем, что под некоторыми штрихами у нас находятся сложные функции , . Каламбур, но это простейшие из сложных функций, и при определенном опыте решения производных Вы будете легко находить их устно.
А пока запишем подробно, согласно правилу , получаем:

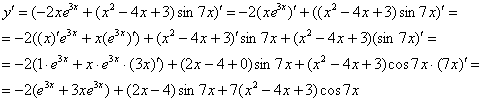
Готово.

Пример 13

Найти производную функции

Это пример для самостоятельного решения (ответ в конце урока).

Пожалуй, хватит на сегодня. Хочется ещё привести пример с дробью и сложной функцией, но такой пример принципиально ничем не отличается от двух последних заданий, единственное отличие – вместо правила  применяем правило .

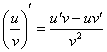Для закрепления темы рекомендую статью Сложные производные. Логарифмическая производная. Помимо рассмотрения дополнительных примеров, есть и новый материал! После изучения третьего урока вы будете очень уверенно себя чувствовать в ходе дальнейшего изучения математического анализа. Если задания покажутся слишком трудными (у всех разный уровень подготовки), то сначала посетите страницу Простейшие типовые задачи с производной, там рассмотрено ещё порядка 15 производных.

Желаю успехов!

Ответы:

Пример 2:

Пример 4:  Указание: перед дифференцированием степень удобно перенести наверх, сменив у показателя знак .

Пример 7: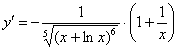

Пример 9:

Пример 11:

Пример 13: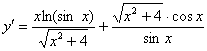

Автор: Емелин Александр

Высшая математика для заочников и не только >>>

(Переход на главную страницу)

Как можно отблагодарить автора?

© Copyright  Александр Емелин, mathprofi.ru, 2010-2025, сделано в Блокноте