


 Высшая математика – просто и доступно!
Высшая математика – просто и доступно!
 Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
Если сайт упал, используйте ЗЕРКАЛО: mathprofi.net
 Наш форум, библиотека и блог: mathprofi.com
Наш форум, библиотека и блог: mathprofi.com
Математические формулы,
таблицы и другие материалы

Высшая математика для чайников, или с чего начать?
 Повторяем школьный курс
Повторяем школьный курс
Аналитическая геометрия:
Векторы для чайников
Скалярное произведение
векторов
Линейная (не) зависимость
векторов. Базис векторов
Переход к новому базису
Векторное и смешанное
произведение векторов
Формулы деления отрезка
в данном отношении
Прямая на плоскости
Простейшие задачи
с прямой на плоскости
Линейные неравенства
Как научиться решать задачи
по аналитической геометрии?
Линии второго порядка. Эллипс
Гипербола и парабола
Задачи с линиями 2-го порядка
Как привести уравнение л. 2 п.
к каноническому виду?
Полярные координаты
Как построить линию
в полярной системе координат?
Уравнение плоскости
Прямая в пространстве
Задачи с прямой в пространстве
Основные задачи
на прямую и плоскость
Треугольная пирамида
Элементы высшей алгебры:
Множества и действия над ними
Основы математической логики
Формулы и законы логики
Уравнения высшей математики
Как найти рациональные корни
многочлена? Схема Горнера
Комплексные числа
Выражения, уравнения и с-мы
с комплексными числами
Действия с матрицами
Как вычислить определитель?
Свойства определителя
и понижение его порядка
Как найти обратную матрицу?
Свойства матричных операций.
Матричные выражения
Матричные уравнения
Как решить систему линейных уравнений?
Правило Крамера. Матричный метод решения системы
Метод Гаусса для чайников
Несовместные системы
и системы с общим решением
Как найти ранг матрицы?
Однородные системы
линейных уравнений
Метод Гаусса-Жордана
Решение системы уравнений
в различных базисах
Линейные преобразования
Собственные значения
и собственные векторы
Квадратичные формы
Как привести квадратичную
форму к каноническому виду?
Ортогональное преобразование
квадратичной формы
Пределы:
Пределы. Примеры решений
Замечательные пределы
Методы решения пределов
Бесконечно малые функции.
Эквивалентности
Правила Лопиталя
Сложные пределы
Пределы последовательностей
Пределы по Коши. Теория
Производные функций:
Как найти производную?
Производная сложной функции. Примеры решений
Простейшие задачи
с производной
Логарифмическая производная
Производные неявной функции,
параметрически заданной
Производные высших порядков
Что такое производная?
Производная по определению
Как найти уравнение нормали?
Приближенные вычисления
с помощью дифференциала
Метод касательных
Функции и графики:
Графики и свойства
элементарных функций
Как построить график функции
с помощью преобразований?
Непрерывность, точки разрыва
Область определения функции
Асимптоты графика функции
Интервалы знакопостоянства
Возрастание, убывание
и экстремумы функции
Выпуклость, вогнутость
и точки перегиба графика
Полное исследование функции
и построение графика
Наибольшее и наименьшее
значения функции на отрезке
Экстремальные задачи
ФНП:
Область определения функции
двух переменных. Линии уровня
Основные поверхности
Предел функции 2 переменных
Повторные пределы
Непрерывность функции 2п
Частные производные
Частные производные
функции трёх переменных
Производные сложных функций
нескольких переменных
Как проверить, удовлетворяет
ли функция уравнению?
Частные производные
неявно заданной функции
Производная по направлению
и градиент функции
Касательная плоскость и
нормаль к поверхности в точке
Экстремумы функций
двух и трёх переменных
Условные экстремумы
Наибольшее и наименьшее
значения функции в области
Метод наименьших квадратов
Интегралы:
Неопределенный интеграл.
Примеры решений
Метод замены переменной
в неопределенном интеграле
Интегрирование по частям
Интегралы от тригонометрических функций
Интегрирование дробей
Интегралы от дробно-рациональных функций
Интегрирование иррациональных функций
Сложные интегралы
Определенный интеграл
Как вычислить площадь
с помощью определенного интеграла?
Что такое интеграл?
Теория для чайников
Объем тела вращения
Несобственные интегралы
Эффективные методы решения
определенных и несобственных
интегралов
Как исследовать сходимость
несобственного интеграла?
Признаки сходимости несобств.
интегралов второго рода
Абсолютная и условная
сходимость несобств. интеграла
S в полярных координатах
S и V, если линия задана
в параметрическом виде
Длина дуги кривой
S поверхности вращения
Приближенные вычисления
определенных интегралов

Метод прямоугольников

Дифференциальные уравнения:
Дифференциальные уравнения первого порядка
Однородные ДУ 1-го порядка
ДУ, сводящиеся к однородным
Линейные неоднородные дифференциальные уравнения первого порядка
Дифференциальные уравнения в полных дифференциалах
Уравнение Бернулли
Дифференциальные уравнения
с понижением порядка
Однородные ДУ 2-го порядка
Неоднородные ДУ 2-го порядка
Линейные дифференциальные
уравнения высших порядков
Метод вариации
произвольных постоянных
Как решить систему
дифференциальных уравнений
Задачи с диффурами
Методы Эйлера и Рунге-Кутты
Числовые ряды:
Ряды для чайников
Как найти сумму ряда?
Признак Даламбера.
Признаки Коши
Знакочередующиеся ряды. Признак Лейбница
Ряды повышенной сложности
Функциональные ряды:
Степенные ряды
Разложение функций
в степенные ряды
Сумма степенного ряда
Равномерная сходимость
Другие функциональные ряды
Приближенные вычисления
с помощью рядов
Вычисление интеграла разложением функции в ряд
Как найти частное решение ДУ
приближённо с помощью ряда?
Вычисление пределов
Ряды Фурье. Примеры решений
Кратные интегралы:
Двойные интегралы
Как вычислить двойной
интеграл? Примеры решений
Двойные интегралы
в полярных координатах
Как найти центр тяжести
плоской фигуры?
Тройные интегралы
Как вычислить произвольный
тройной интеграл?

Криволинейные интегралы
Интеграл по замкнутому контуру
Формула Грина. Работа силы
Поверхностные интегралы
Элементы векторного анализа:
Основы теории поля
Поток векторного поля
Дивергенция векторного поля
Формула Гаусса-Остроградского
Циркуляция векторного поля
и формула Стокса
Комплексный анализ:
ТФКП для начинающих
Как построить область
на комплексной плоскости?
Линии на С. Параметрически
заданные линии
Отображение линий и областей
с помощью функции w=f(z)
Предел функции комплексной
переменной. Примеры решений
Производная комплексной
функции. Примеры решений
Как найти функцию
комплексной переменной?
Конформное отображение
Решение ДУ методом
операционного исчисления
Как решить систему ДУ
операционным методом?
Теория вероятностей:
Основы теории вероятностей
Задачи по комбинаторике
Задачи на классическое
определение вероятности
Геометрическая вероятность
Задачи на теоремы сложения
и умножения вероятностей
Зависимые события
Формула полной вероятности
и формулы Байеса
Независимые испытания
и формула Бернулли
Локальная и интегральная
теоремы Лапласа
Статистическая вероятность
Случайные величины.
Математическое ожидание
Дисперсия дискретной
случайной величины
Функция распределения
Геометрическое распределение
Биномиальное распределение
Распределение Пуассона
Гипергеометрическое
распределение вероятностей
Непрерывная случайная
величина, функции F(x) и f(x)
Как вычислить математическое
ожидание и дисперсию НСВ?
Равномерное распределение
Показательное распределение
Нормальное распределение
Система случайных величин
Зависимые и независимые
случайные величины
Двумерная непрерывная
случайная величина
Зависимость и коэффициент
ковариации непрерывных СВ
Математическая статистика:
Математическая статистика
Дискретный вариационный ряд
Интервальный ряд
Мода, медиана, средняя
Показатели вариации
Формула дисперсии, среднее
квадратическое отклонение,
коэффициент вариации
Асимметрия и эксцесс
эмпирического распределения
Статистические оценки
и доверительные интервалы
Оценка вероятности
биномиального распределения
Оценки по повторной
и бесповторной выборке
Статистические гипотезы
Проверка гипотез. Примеры
Гипотеза о виде распределения
Критерий согласия Пирсона
Группировка данных. Виды группировок. Перегруппировка
Общая, внутригрупповая
и межгрупповая дисперсия
Аналитическая группировка
Комбинационная группировка
Эмпирические показатели
Как вычислить линейный
коэффициент корреляции?
Уравнение линейной регрессии
Проверка значимости линейной
корреляционной модели
Модель пАрной регрессии.
Индекс детерминации
Нелинейная регрессия. Виды и
примеры решений
Коэффициент ранговой
корреляции Спирмена
Коэф-т корреляции Фехнера
Уравнение множественной
линейной регрессии

Ряды динамики. Базисные,
цепные и средние показатели
Сглаживание временнОго ряда
Не нашлось нужной задачи?
Сборники готовых решений!
Не получается пример?
Задайте вопрос на форуме!
>>> mathprofi
Часто задаваемые вопросы
Гостевая книга
Отблагодарить автора >>>
Заметили опечатку / ошибку?
Пожалуйста, сообщите мне об этом
Относительная частота события
и статистическое определение вероятности
Сегодня мы завершаем изучение первого раздела теории вероятностей, который посвящён основным подходам к определению вероятности, теоремам сложения и умножения событий, а также их основным следствиям. В учебной литературе статистическое определение вероятности обычно рассматривается в первой же главе, но вот мне показалось удачным отложить этот вопрос на заключительный урок по теме. Давайте вспомним, с чего всё начиналось:
Вероятность наступления события ![]() в некотором испытании – есть отношение
в некотором испытании – есть отношение ![]() , где:
, где:
![]() – общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий;
– общее число всех равновозможных, элементарных исходов этого испытания, которые образуют полную группу событий;
![]() – количество элементарных исходов, благоприятствующих событию
– количество элементарных исходов, благоприятствующих событию ![]() .
.
О некоторых недостатках классического определения вероятности заходила речь в статье Геометрическое определение вероятности, но это только верхушка айсберга, и сейчас данный вопрос получит интереснейшее продолжение. Начнём опять же с бесхитростных примеров 1-го урока по теории вероятностей:
![]() – вероятность того, что в результате броска монеты выпадет «орёл»;
– вероятность того, что в результате броска монеты выпадет «орёл»;
![]() – вероятность того, что в результате броска игральной кости выпадет 5 очков;
– вероятность того, что в результате броска игральной кости выпадет 5 очков;
![]() – вероятность того, что из колоды будет извлечена трефа
– вероятность того, что из колоды будет извлечена трефа
Внимательный читатель заметил, что все комментарии о вероятностях сформулированы в будущем времени. И это не случайность – классическое определение, как правило, оценивает вероятность ДО проведения испытаний и даже без их фактического проведения. То есть, монета ещё не подброшена, а вероятность появления орла мы уже прекрасно знаем. Можно дать зарок никогда не брать в руки кубик либо колоду карт, однако, вероятности событий ![]() беспроблемно рассчитываются и без этого.
беспроблемно рассчитываются и без этого.
Примечание: однако, в отсутствии информации о результате испытания фразу «Вероятность того, что монета упала орлом» (например) всё же нельзя признать некорректной. То есть классическое определение может оценивать вероятность и после реального опыта.
Почему такое возможно? Такое возможно потому, что все элементарные исходы известны и подсчитаны заранее:
орёл и решка – итого 2 элементарных исхода;
1, 2, 3, 4, 5, 6 – 6 элементарных исходов;
6, 7, 8, 9, 10, В, Д, К, Т каждой масти – всего 36 карт.
Кроме того, для применения классического определения вероятности необходима равновозможность элементарных исходов (см. определение). Равновозможность выпадения граней монеты либо кубика обуславливается симметрией и несмещённым центром тяжести, колода же карт должна быть полной, некраплёной и хорошо перемешанной.
И всё было бы ладно, но в реальной жизни подобные модели встречаются нечасто. В большинстве ситуаций элементарные исходы перечислить затруднительно или невозможно, и ещё труднее обосновать их равновозможность. Простой пример:
Штирлиц пошёл в лес за грибами. Найти вероятность того, что он найдёт подберёзовик.
Совершенно понятно, что все грибы в лесу (общее количество элементарных исходов) пересчитать практически невозможно, а значит, классическое определение вероятности не срабатывает. И даже если группа разведчиков учтёт все грибы в небольшой роще, классифицирует их по видам, то препятствием станет неравновозможность исходов. Почему? Поляна мухоморов намного заметнее, чем замаскировавшиеся подберёзовики. …Таааак, кто это там на задней парте предложил покрасить в один цвет? =)
Кстати, каверзная задачка на счёт равновозможности была в конце урока о теоремах Лапласа. Краткая суть состоит в следующем: если в городе проживает примерно равное количество мужчин и женщин (которых подсчитать значительно проще =)), то это ещё не значит, что вероятность встретить на улице мужчину либо женщину равна 1/2.
Вновь обратим внимание на шаблонные формулировки стандартных задач:
«Стрелок попадает в мишень с вероятностью 0,8»;
«Вероятность изготовления бракованной детали на данном станке составляет 0,05».
Возникает вопрос, откуда взялись эти значения? И ответ здесь один: данные вероятности могли получиться только на основе ранее проведённых опытов.
Относительная частота события и статистическая вероятность
Относительной частотой события ![]() называют отношение числа испытаний
называют отношение числа испытаний ![]() , в которых данное событие появилось, к общему числу
, в которых данное событие появилось, к общему числу ![]() фактически проведённых испытаний:
фактически проведённых испытаний:
![]() , или короче:
, или короче: ![]()
Относительная частота наряду с вероятностью является одним из ключевых понятий тервера, но если классическое либо геометрическое определение вероятности не требуют проведения испытаний, то относительная частота рассчитывается исключительно ПОСЛЕ опытов на основе фактически полученных данных.
В том случае, если серии испытаний проводятся в неизменных условиях, то относительная частота обнаруживает свойство устойчивости, то есть колеблется около определённого значения.
Пусть некий профессиональный стрелок произвёл 100 выстрелов по мишени и попал 83 раза. Тогда относительная частота поражения цели составит: ![]() .
.
Предположим, что тот же самый стрелок в точно такой же «форме» и в приблизительно таких же условиях снова провёл серию из 100 выстрелов. Вероятно ли, что он снова попадёт 83 раза? Не очень. Но количество попаданий вряд ли будет сильно отличаться от предыдущего результата. Пусть, например, стрелок попал 79 раз. Тогда относительная частота поражения цели составит: ![]() .
.
В третьей серии из 100 выстрелов, проведённой при похожих обстоятельствах, данный стрелок попал 81 раз, ![]() и т.д.
и т.д.
Иногда могут случаться блестящие серии более 90 попаданий, иногда «провалы», но среднее количество попаданий будет варьироваться около 80. И когда количество фактически проведённых испытаний станет достаточно большим, то речь зайдёт о статистической вероятности. Если в одинаковых (примерно одинаковых) условиях проведено достаточно много испытаний, то за статистическую вероятность события принимают относительную частоту данного события либо близкое число.
Предположим, что на протяжении нескольких лет наш спортсмен, сохраняя стабильный уровень подготовки, совершил 10000 выстрелов и попал 8037 раз. Относительная частота поражения цели составит: ![]() и за статистическую вероятность его результативности целесообразно принять
и за статистическую вероятность его результативности целесообразно принять ![]() , которая становится теоретической оценкой, например, перед грядущими соревнованиями.
, которая становится теоретической оценкой, например, перед грядущими соревнованиями.
Представьте, что во время лекции этот профессионал зашёл с винтовкой в аудиторию и прицелился. Теперь вам должен стать окончательно понятен смысл фразы «Стрелок попадает в мишень с вероятностью 0,8» =) =)
Именно так собирается богатая спортивная статистика в различных видах спорта.
Аналогичная история с утверждением «Вероятность изготовления бракованной детали на данном станке равна 0,05». Эту оценку невозможно получить с помощью классического определения вероятности – она следует только из практики! Если на станке произведены десятки тысяч деталей и на каждую, скажем, тысячу выпущенных деталей, приходится в среднем 50 бракованных, то в качестве статистической вероятности брака принимается значения ![]() .
.
В Задаче 2 урока Локальная и интегральная теоремы Лапласа фигурировала вероятность рождения мальчика ![]() . Откуда взялось данное число? Из многолетнего подсчёта фактически рождённых детей в определённом регионе. В указанной статье мы выяснили, что это вовсе не значит, что среди 100 новорожденных будет ровно 52 мальчика. В следующей сотне рождённых их может оказаться, например, 45, и относительная частота
. Откуда взялось данное число? Из многолетнего подсчёта фактически рождённых детей в определённом регионе. В указанной статье мы выяснили, что это вовсе не значит, что среди 100 новорожденных будет ровно 52 мальчика. В следующей сотне рождённых их может оказаться, например, 45, и относительная частота ![]() будет далека от истины. Но если рассмотреть выборку в тысячи и десятки тысяч младенцев, то
будет далека от истины. Но если рассмотреть выборку в тысячи и десятки тысяч младенцев, то ![]() отклонится от
отклонится от ![]() совсем-совсем незначительно. И это уже не случайность. Как известно, такое соотношение новорожденных сложилось эволюционно – по причине бОльшей смертности мужчин.
совсем-совсем незначительно. И это уже не случайность. Как известно, такое соотношение новорожденных сложилось эволюционно – по причине бОльшей смертности мужчин.
В учебном пособии В.Е. Гмурмана есть весьма удачный пример, в котором продемонстрировано, как при подбрасывании монеты относительная частота появления орла приближается к своей вероятности ![]() (полученной по классическому определению):
(полученной по классическому определению):
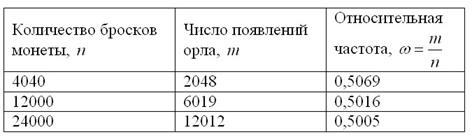
Какой можно сделать вывод? С увеличением количества независимых испытаний случайность превращается в закономерность. Однако следует помнить, что порядок выпадения орлов непредсказуем, о чём я подробно рассказывал на уроке Независимые испытания и формула Бернулли.
Вернёмся к европейской рулетке с 18 красными, 18 чёрными секторами и 1 зеро. В самом примитивном варианте игры: ставим на «красное» или «чёрное», и если шарик остановился на секторе другого цвета (вероятность ![]() ) – ставка проигрывается. В случае успеха – удваиваемся (вероятность
) – ставка проигрывается. В случае успеха – удваиваемся (вероятность ![]() ).
).
В отдельно взятом сеансе игры отдельно взятый человек может выиграть, причём выиграть по-крупному. Это случайность. Но, совершая миллионы оборотов, рулетка на протяжении веков приносит неизменную прибыль владельцам казино. И это – закономерность. Существует байка о том, что крупный выигрыш не отдадут, а если и отдадут, то «вы с ним не дойдёте до дома». Чистая «киношная» фантазия. Да, кому-то повезло, но сколько проиграется?! К тому же человек, посещающий подобные заведения, с большой вероятностью придёт снова и «сольёт» ещё больше. А чтобы он вернулся, казино, скорее наоборот – создаст максимальный комфорт и безопасность для «счастливчика».
Другой, во многом условный, пример: пусть в некой лотерее приняло участие ![]() билетов, из которых
билетов, из которых ![]() выиграли хоть какой-то приз. Таким образом, относительная частота выигрыша составила:
выиграли хоть какой-то приз. Таким образом, относительная частота выигрыша составила: ![]() . Поскольку билетов продано очень много, то с большой вероятностью можно утверждать, что в будущем при сопоставимых объемах продаж доля выигравших билетов будет примерно такой же, и за статистическую вероятность выигрыша удобно принять значение
. Поскольку билетов продано очень много, то с большой вероятностью можно утверждать, что в будущем при сопоставимых объемах продаж доля выигравших билетов будет примерно такой же, и за статистическую вероятность выигрыша удобно принять значение ![]() .
.
Организатор лотереи знает, что из миллиона проданных билетов выиграют около 300 тысяч с небольшим отклонением. И это закономерность. Но всем участникам лотереи достаётся…. – правильно, случайность! То есть, если вы купите 10 билетов, то это ещё не значит, что выиграют 3 билета. Так, например, выигрыш только по одному билету – есть событие очень даже вероятное, по формуле Бернулли:
![]()
А если учесть тот факт, что львиная доля выигрышей – сущая мелочь, то картина вырисовывается совсем унылая, ибо маловозможные события не происходят. Ситуацию спасают красочные телевизионные розыгрыши и различные психологические трюки.
Желающие могут самостоятельно исследовать вероятность выигрыша в различные лотереи – вся статистика есть в свободном доступе. Особо рекомендую подсчитать вероятность крупного выигрыша.
Практическая часть урока будет тесно связана с только что изложенным материалом:
Вероятность отклонения относительной частоты от вероятности
Вероятность того, что в ![]() независимых испытаниях относительная частота
независимых испытаниях относительная частота ![]() события
события ![]() отклонится от вероятности
отклонится от вероятности ![]() (появления данного события в каждом испытании) не более чем на
(появления данного события в каждом испытании) не более чем на ![]() , приблизительно равна:
, приблизительно равна:
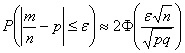 , где
, где 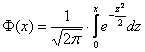 – функция Лапласа.
– функция Лапласа.
Собственно, эта формула и выведена из интегральной теоремы Лапласа.
Итак, расклад следующий: в распоряжении имеется вероятность ![]() наступления события
наступления события ![]() , которая предварительно получена с помощью классического/геометрического определения или посредством серьёзной статистической оценки. Планируется провести
, которая предварительно получена с помощью классического/геометрического определения или посредством серьёзной статистической оценки. Планируется провести ![]() независимых испытаний, в которых событие
независимых испытаний, в которых событие ![]() может наступить некоторое количество раз, причём значение
может наступить некоторое количество раз, причём значение ![]() , разумеется, предсказать нельзя. Полученная относительная частота
, разумеется, предсказать нельзя. Полученная относительная частота ![]() может оказаться как больше, так и меньше вероятности
может оказаться как больше, так и меньше вероятности ![]() (поэтому нужен знак модуля).
(поэтому нужен знак модуля).
Требуется найти вероятность того, что в серии из ![]() независимых испытаний, расхождение между относительной частотой и теоретической вероятностью
независимых испытаний, расхождение между относительной частотой и теоретической вероятностью ![]() , будет не больше, чем заранее заданное число, например, не больше, чем
, будет не больше, чем заранее заданное число, например, не больше, чем ![]() (один процент).
(один процент).
Начнём с самых маленьких :=)
Задача 1
В некотором регионе в результате многолетнего статистического исследования установлена вероятность рождения мальчика ![]() . С какой вероятностью можно утверждать, что среди следующей тысячи новорожденных, относительная частота появления мальчика отклонится от соответствующей вероятности не более чем на 0,02?
. С какой вероятностью можно утверждать, что среди следующей тысячи новорожденных, относительная частота появления мальчика отклонится от соответствующей вероятности не более чем на 0,02?
Решение: используем формулу 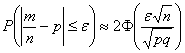
По условию: ![]()
Таким образом:
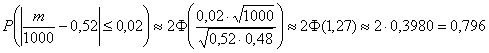 – искомая вероятность.
– искомая вероятность.
Напоминаю, что значения функции Лапласа можно найти по соответствующей таблице или с помощью расчётного макета (пункт 5).
Ответ: ![]()
Каков смысл полученного результата? Если рассмотреть достаточно много групп по 1000 новорожденных в каждой, то примерно в 79,6% этих групп доля мальчиков будет находиться в пределах:
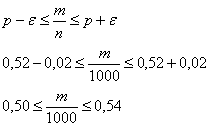
Или, умножая все три части на тысячу: от 500 до 540 мальчиков.
На самом деле рассмотренная задача эквивалентна следующей: «Найти вероятность того, что среди 1000 новорожденных будет от 500 до 540 мальчиков, если вероятность рождения мальчика равна 0,52». А эта задача как раз и решается через известную вам интегральную теорему Лапласа.
Посмотрим на правую часть формулы 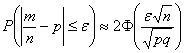 и проанализируем, как при прочих равных условиях рассматриваемая вероятность зависит от размера выборки?
и проанализируем, как при прочих равных условиях рассматриваемая вероятность зависит от размера выборки?
При росте «эн», дробь ![]() будет увеличиваться, а, как вы знаете,
будет увеличиваться, а, как вы знаете, ![]() . То есть, вероятность отклонения
. То есть, вероятность отклонения ![]() рано или поздно приблизится к единице. И это неудивительно – как неоднократно показано в предыдущих примерах, при росте
рано или поздно приблизится к единице. И это неудивительно – как неоднократно показано в предыдущих примерах, при росте ![]() относительная частота события
относительная частота события ![]() всё ближе и ближе стремится к вероятности
всё ближе и ближе стремится к вероятности ![]() данного события, а значит, при достаточно большом количестве испытаний разница
данного события, а значит, при достаточно большом количестве испытаний разница ![]() практически достоверно будет не больше наперёд заданного числа
практически достоверно будет не больше наперёд заданного числа ![]() .
.
Наоборот – при уменьшении «эн» дробь ![]() тоже будет уменьшаться, следовательно, значение
тоже будет уменьшаться, следовательно, значение 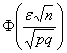 будет приближаться к нулю
будет приближаться к нулю ![]() . Нетрудно понять, что при слишком малой выборке теорема Лапласа работать перестанет. И действительно – ведь все
. Нетрудно понять, что при слишком малой выборке теорема Лапласа работать перестанет. И действительно – ведь все ![]() детей в семье могут вообще оказаться девочками. Такое бывает.
детей в семье могут вообще оказаться девочками. Такое бывает.
Пара задач для самостоятельного решения:
Задача 2
Производится некоторый опыт, в котором случайное событие ![]() может появиться с вероятностью 0,6. Опыт повторяют в неизменных условиях
может появиться с вероятностью 0,6. Опыт повторяют в неизменных условиях ![]() раз. Определить вероятность того, что в 800 независимых испытаниях относительная частота появления события
раз. Определить вероятность того, что в 800 независимых испытаниях относительная частота появления события ![]() отклонится от вероятности не более чем: а) на 0,05, б) на 0,03
отклонится от вероятности не более чем: а) на 0,05, б) на 0,03
Условие сформулировано в общем виде, как оно чаще всего и бывает. Ещё раз повторим суть задания: проводится ![]() опытов, в результате чего событие
опытов, в результате чего событие ![]() наступит
наступит ![]() раз – сколько именно, предугадать невозможно. Относительная частота составит
раз – сколько именно, предугадать невозможно. Относительная частота составит ![]() . С другой стороны, известна вероятность
. С другой стороны, известна вероятность ![]() события
события ![]() , которая установлена ранее с помощью классического/геометрического определения или путём сбора солидной статистики. Требуется найти вероятность того, что относительная частота отклонится от вероятности, не более чем на
, которая установлена ранее с помощью классического/геометрического определения или путём сбора солидной статистики. Требуется найти вероятность того, что относительная частота отклонится от вероятности, не более чем на ![]() :
: ![]() В чём смысл? С найденной вероятностью
В чём смысл? С найденной вероятностью 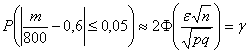 можно утверждать, что относительная частота будет заключена в следующих пределах:
можно утверждать, что относительная частота будет заключена в следующих пределах:
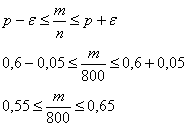
Или в абсолютном количестве появлений события ![]() :
:
![]()
Надо сказать, что границы достаточно вольные и вероятность ![]() должна получиться большой. Если же наперёд заданная точность составит
должна получиться большой. Если же наперёд заданная точность составит ![]() , то промежуток сократится:
, то промежуток сократится: ![]() , и, понятно, что вероятность
, и, понятно, что вероятность ![]() данного события будет меньше.
данного события будет меньше.
Следующий пример для самых мудрых участников лотереи :)
Задача 3
Вероятность выигрыша в лотерею равна 0,3. Продано 600000 билетов. Найти вероятность того, что относительная частота выигрыша отклонится от вероятности выигрыша не более чем на ![]() .
.
Иными словами, требуется найти вероятность того, что относительная частота выигрыша будет находиться в пределах: ![]() (то есть выиграют от
(то есть выиграют от ![]() до
до ![]() билетов).
билетов).
Эта информация очень важнА для корректного распределения призового фонда. Но, повторюсь, пример достаточно условный, т.к. не учитывает правила и ограничения той или иной лотереи.
Краткое решение и ответы в конце урока.
На практике не менее популярна и обратная задача:
Как определить, сколько нужно провести испытаний 
чтобы с заранее заданной вероятностью  обеспечить желаемую точность
обеспечить желаемую точность 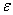 ?
?
В предыдущем примере получена довольно высокая вероятность ![]() того, что количество выигравших билетов окажется в достаточно узком интервале:
того, что количество выигравших билетов окажется в достаточно узком интервале: ![]() билетов
билетов ![]() относительно наивероятнейшего количества
относительно наивероятнейшего количества ![]() .
.
Но, конечно же, хочется, чтобы вероятность ![]() была побольше:
была побольше:
Задача 4
Вероятность выигрыша в лотерею равна 0,3. Сколько билетов должно участвовать в розыгрыше, чтобы с вероятностью не меньшей чем ![]() , можно было ожидать, что относительная частота выигрыша отклонится от теоретической вероятности не более чем на
, можно было ожидать, что относительная частота выигрыша отклонится от теоретической вероятности не более чем на ![]() ?
?
Решение: используем ту же формулу 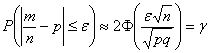 .
.
В нашем распоряжении находятся следующие величины:
![]()
По условию, требуется найти такое количество билетов ![]() , чтобы с вероятностью не меньшей чем
, чтобы с вероятностью не меньшей чем ![]() разница
разница ![]() составила не более чем
составила не более чем ![]() . Ну, а коль скоро с вероятностью «не меньшей», то задачу следует разрулить через нестрогое неравенство:
. Ну, а коль скоро с вероятностью «не меньшей», то задачу следует разрулить через нестрогое неравенство:
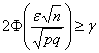
Подставляем известные значения:
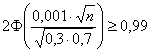
Делим обе части на два:
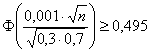
По таблице значений функции ![]() либо с помощью расчётного макета (пункт 5*) по известному значению функции
либо с помощью расчётного макета (пункт 5*) по известному значению функции ![]() находим соответствующий аргумент:
находим соответствующий аргумент: ![]() . Таким образом:
. Таким образом:
![]()
Возведём обе части в квадрат:
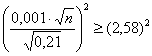
![]()
И финальный штрих:
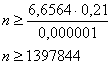
Ответ: для того, чтобы с вероятностью не меньшей чем ![]() , можно было ожидать, что
, можно было ожидать, что ![]() , в розыгрыше должно участвовать не менее 1397844 билетов.
, в розыгрыше должно участвовать не менее 1397844 билетов.
Но это ещё нужно столько продать =) Или же аппетит ![]() придётся поубавить. Или пожертвовать точностью, то есть увеличить
придётся поубавить. Или пожертвовать точностью, то есть увеличить ![]() .
.
Представим ответ в абсолютных значениях:
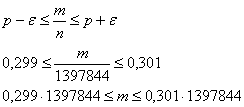
То есть, в 99% аналогичных розыгрышей количество выигравших билетов будет заключено в пределах от ![]() до
до ![]() .
.
Кстати, выполним проверку, решив прямую задачу:
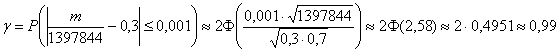 , что и требовалось проверить.
, что и требовалось проверить.
Заключительная миниатюра для самостоятельного решения:
Задача 5
Проводится некоторый опыт, в котором случайное событие ![]() может появиться с вероятностью 0,4. Определить, сколько опытов нужно провести, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события
может появиться с вероятностью 0,4. Определить, сколько опытов нужно провести, чтобы с вероятностью большей, чем 0,9 можно было ожидать отклонения относительной частоты появления события ![]() от
от ![]() не более чем на 0,05
не более чем на 0,05
Не ленимся ;-) Ответ в таких задачах следует округлять до бОльшего натурального значения! Краткое решение и ответ внизу страницы.
Первый цикл уроков по теории вероятностей подошёл к концу и даже начал плавно переходить в математическую статистику, так, если в рассмотренной задаче значение ![]() не известно, то это уже статистическая задача об оценке этой вероятности.
не известно, то это уже статистическая задача об оценке этой вероятности.
И я уже хотел поставить традиционное пожелание «Везения в главном», но вдруг задумался…. Имеет ли в нашей жизни значение случайность? Безусловно! Нет, я не преуменьшаю значение системной и упорной работы, после которой следуют закономерные результаты. Однако и везение играет немаловажную роль: встретить хороших друзей, встретить «своего» человека, найти деятельность по душе и т.д. – всё это нередко происходит благодаря случаю….
Жду вас снова и до скорых встреч!
Решения и ответы:
Задача 2: Решение: используем формулу 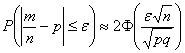 .
.
В данной задаче: ![]()
а) Если ![]() , то:
, то:
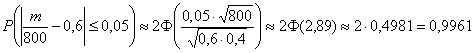 – вероятность, того, что при 800 испытаниях относительная частота появления события
– вероятность, того, что при 800 испытаниях относительная частота появления события ![]() отклонится от вероятности данного события не более чем на 0,05.
отклонится от вероятности данного события не более чем на 0,05.
Это событие является практически достоверным.
б) Если ![]() , то:
, то:
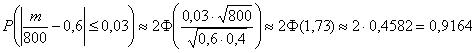 – вероятность, того, что при 800 испытаниях относительная частота появления события
– вероятность, того, что при 800 испытаниях относительная частота появления события ![]() отклонится от вероятности данного события не более чем на 0,03.
отклонится от вероятности данного события не более чем на 0,03.
Ответ: ![]()
Задача 3: Решение: используем формулу 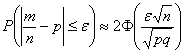 .
.
В данной задаче: ![]()
Таким образом:
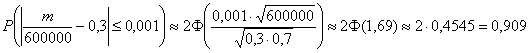 – вероятность, того, что относительная частота выигрыша отклонится от теоретической вероятности не более чем на 0,001.
– вероятность, того, что относительная частота выигрыша отклонится от теоретической вероятности не более чем на 0,001.
Ответ: ![]()
Задача 5: Решение: используем формулу 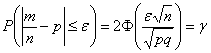 .
.
В данном случае: ![]()
Таким образом:
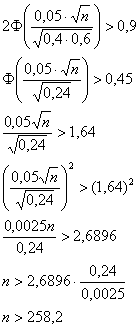
Ответ: необходимо произвести не менее 259 опытов.
Автор: Емелин Александр
Высшая математика для заочников и не только >>>
(Переход на главную страницу)

 Карта сайта
Карта сайта

 © Copyright
© Copyright